激光雷达基本原理
-
- 激光雷达工作原理
激光雷达根据测量原理可以分为三角法激光雷达、脉冲法激光雷达、相干法激光雷达。最常用的是脉冲激光雷达。基于脉冲法的激光雷达利用光速测距。激光发射器发射激光脉冲,计时器记录发射时间;脉冲经物体反射后由接收器接收,计时器记录接收时间;时间差乘上光速除以2得到距离。
-
- 激光雷达系统
组成
(1)发射单元:激光器、发射光学系统,发射激光束探测信号;
(2)接收单元:接收光学系统、光学滤光装置、光电探测器。(接收反射的激光信号即回波信号);
(3)控制单元:控制器、逻辑电路;
(4)信号处理单元:信号处理、数据校准与输出
优点与不足
激光雷达的优点:
- 具有很高的分辨率
- 抗干扰能力强
- 获取的信息量丰富
- 可全天候工作
激光雷达的不足:
- 受极度恶劣天气和环境影响(烟雾、粉尘、雨雪、沙尘等)
- 价格较贵,大部分产品处于万元级别
性能指标
激光波长:目前市场上激光雷达最常用的波长是905nm和1550 nm。1550nm波长激光雷达传感器可以以更高的功率运行,以提高探测范围,同时对于雨雾的穿透力更强。
测量距离:激光雷达所标称的距离大多以90%反光率的漫反射物体(如白纸)作为测试基准。激光雷达的测距与目标的反射率相关。目标的反射率越高则测量的距离越远。因此在查看激光雷达的探测距离时要知道该测量距离是目标反射率为多少时的探测距离。
扫描频率:一秒内进行多少次测距输出。较高的扫描频率可以确保安装激光雷达的机器人实现较快速度的运动,并且保证地图构建的质量。但要提高扫描频率并不只是简单的加速激光雷达内部扫描电机旋转这么简单,对应的需要提高测距采样率。
角分辨率:角分辨率是扫描仪分辨目标的能力,角分辨率越小,则表明能够分辨的目标越小,这样测量出的点云数据就越细腻。包括垂直分辨率和水平分辨率,水平方向上由电机带动,所以水平分辨率可以做得很高。垂直分辨率是与发射器几何大小相关,也与其排布有关系,就是相邻两个发射器间隔做得越小,垂直分辨率也就会越小。
视场角大小(FOV):激光束通过扫描装置所能达到的最大角度范围,包括水平视场角和垂直视场角。垂直视场角一般在30°~50°之间,机械式的水平视场角一般是360°,固态式水平视场角一般在80~120°之间。
雷达线束:常见的激光雷达的线束有16线、32线、64线等。多线激光雷达就是通过多个激光发射器在上的分布,通过电机的旋转形成多条线束的扫描。
分类
基于TOF法的激光雷达可以分为机械式激光雷达、MEMS激光雷达、相控阵激光雷达、FLASH激光雷达。市场上现在应用多的是机械式激光雷达,即使用机械部件旋转来改变发射角度从而测量激光发出和收到回波的时间差,确定目标的方位和距离。
-
- 点云组织形式
三维点云数据用于表征目标表面的点的集合,但是各个离散点之间并没有拓扑关系,一般需要通过建立点云的空间索引来实现基于邻域关系的快速查找。在三维点云数据中用的较为广泛的两种结构分别是Kdtree和Octree。
Kdtree
原理
Kdtree是一种划分k维数据空间的数据结构,在一个K维数据集合上构建一棵Kdtree代表了对该K维数据集合构成的K维空间的一个划分,即树中的每个结点就对应了一个K维的超矩形区域。主要用于多维空间关键数据的搜索。
创建
Kdtree的创建就是按照某种顺序将无序化的点云进行有序化排列,方便进行快捷高效的检索。算法流程如下:
(1) 在K维数据集合中选择具有最大方差的维度,然后在该维度上选择中值m为中心对该数据集合进行划分,得到两个子集合;同时创建一个树结点node,用于存储;
(2)对两个子集合重复(1)步骤的过程,直至所有子集合都不能再划分为止;如果某个子集合不能再划分时,则将该子集合中的数据保存到叶子结点。
根据上述算法步骤,以二维数据创建Kdtree为例,输入数据列表为{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)};划分的二维分割图如下:
首先统计X和Y方向上的方差,选取方差较大的X维度作为初始分割轴,对X轴上的数值{2,5,9,4,8,7}取中值X=7作为分割线,生成左子树{(2,3),(5,4),(4,7)},生成右子树{(9,6),(8,1)},更新分割轴Y,分别在左右子树中找到中位数(5,4)和(9,6),依次迭代如下图:
搜索
Kdtree的搜索方法有以下两种:
半径搜索:给定搜索点和搜索距离的阈值,从数据集中找出所有与搜索点距离小于阈值的数据;
最近邻搜索:给定查询点和正整数K,从数据集中找到距离查询点最近的K个数据,当K=1时,就是最近邻搜索。
混合搜索。
以最近邻搜索算法为例,其流程如下:
(1)将查询数据Q从根结点开始,按照Q与各个结点的比较结果向下访问Kdtree,直至达到叶子结点。
其中Q与结点的比较指的是将Q对应于结点中的k维度上的值与中值m进行比较,若Q(k) < m,则访问左子树,否则访问右子树。达到叶子结点时,计算Q与叶子结点上保存的数据之间的距离,记录下最小距离对应的数据点,记为当前最近邻点和最小距离Distance。
(2)进行回溯操作,该操作是为了找到离Q更近的“最近邻点”。即判断未被访问过的分支里是否还有离Q更近的点,它们之间的距离小于Distance。
如果Q与其父结点下的未被访问过的分支之间的距离小于Distance,则认为该分支中存在离P更近的数据,进入该结点,进行(1)步骤一样的查找过程,如果找到更近的数据点,则更新为当前的最近邻点,并更新Distance。
如果Q与其父结点下的未被访问过的分支之间的距离大于Distance,则说明该分支内不存在与Q更近的点。
回溯的判断过程是从下往上进行的,直到回溯到根结点时已经不存在与P更近的分支为止。
Octree
原理
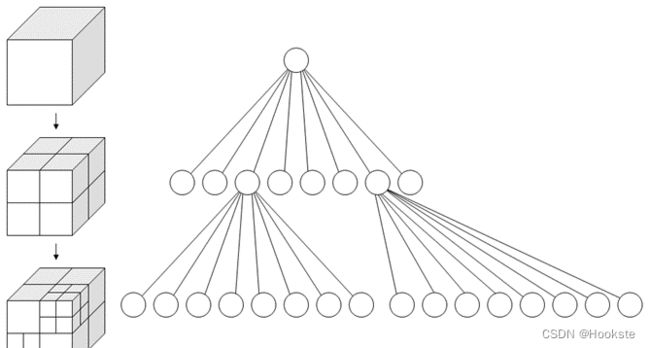
Octree是一种用于描述三维空间的树状数据结构。八叉树的每个节点表示一个正方体的体积元素,每个节点有八个子节点,将八个子节点所表示的体积元素加在一起就等于父节点的体积。
通过对三维空间的几何实体进行体元剖分,每个体元具有相同的时间和空间复杂度,通过循环递归的划分方法对大小为(2n∗2n∗2n) 的三维空间的几何对象进行剖分,从而构成一个具有根节点的方向图。在八叉树结构中如果被划分的体元具有相同的属性,则该体元构成一个叶节点;否则继续对该体元剖分成8个子立方体,依次递剖分,对于(2n∗2n∗2n)大小的空间对象,最多剖分n 次,如下图所示:
创建
(1)设定最大递归深度
(2)找出场景的最大尺寸,并以此尺寸建立第一个立方体
(3)依序将单位元元素丢入能被包含且没有子节点的立方体
(4)若没有达到最大递归深度,就进行细分八等份,再将该立方体所装的单位元元素全部分担给八个子立方体
(5)若发现子立方体所分配到的单位元元素数量不为零且跟父立方体是一样的,则该子立方体停止细分,因为跟据空间分割理论,细分的空间所得到的分配必定较少,若是一样数目,则再怎么切数目还是一样,会造成无穷切割的情形。
(5)重复3,直到达到最大递归深度。
Octree的叶子节点代表了分辨率最高的情况。例如分辨率设成0.01m,那么每个叶子就是一个1cm见方的小方块。如下图所示:
当分辨率较高时,方块很小;分辨率较低时,方块很大。以斯坦福课程中的兔子模型为例: