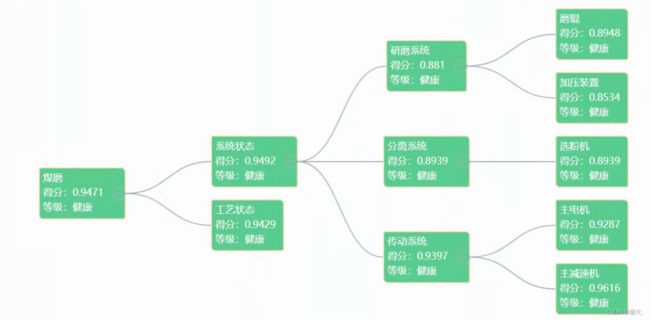
基于设备状态测点进行健康度评估的算法

效果：

示例算法：

# -*-coding:utf-8-*-
# 设备健康度评价算法
import json

import numpy as np
import math

# 归一化Normalized-健康度评价
from numpy import array, around

np.set_printoptions(precision=4, suppress=False)

# 最小阈值、最大阈值、标准值、实时值、数据指标类型
# 标准化  基于指标类型计算
def normalization(minValue, maxValue, tandardValue, value, type):
    if minValue == None or maxValue == None or tandardValue == None or value == None or type == None:
        return None
    # 标准值指标
    if type == 3:
        if minValue <= value < tandardValue:
            return (value - minValue) / (tandardValue - minValue)
        elif tandardValue <= value <= maxValue:
            return (maxValue - value) / (maxValue - tandardValue)
        else:
            return 0.0
    # 正向指标(越大越好)
    elif type == 2:
        health_value = (value - minValue) / (maxValue - minValue)
        if health_value > 1:
            health_value = 1
        return health_value
    # 逆向指标(越小越好)
    elif type == 1:
        health_value = 1 - (value - minValue) / (maxValue - minValue)
        if health_value > 1:
            health_value = 1
        return health_value


# 指标健康度
def indicator_health(args):
    data_array = array(args['data'])
    rows = data_array.shape[0]
    health_list = []
    for i in range(0, rows):
        # 指标数据（最小阈值，最大阈值，标准值，测量值,报警值,指标类型）
        health = normalization(data_array[i][0], data_array[i][1], data_array[i][2], data_array[i][3], data_array[i][5])
        # print('指标测量数据：{0}----{1}'.format(data_array[i], health))
        if health == None:
            health_list.append(None)
        else:
            if health < 0:
                health = 0
            health_list.append(round(health, 4))
    print('指标健康度：{0}'.format(health_list))
    return array(health_list).tolist()


# 层次权重
def hierarchy_weight(args):
    data_array = array(args['data'])
    # 特征值计算
    lamda = np.linalg.eig(data_array)
    # for i in range(len(lamda[0])):
    # print('特征值：{0}\n对应的特征向量：\n{1}\n'.format(lamda[0][i], np.transpose([lamda[1][:, i]])))
    index = np.argmax(lamda[0])
    lamda_max = np.real(lamda[0][index])
    vector = lamda[1][:, index]
    # 特征向量
    vector_final = np.transpose((np.real(vector)))
    # 归一化
    one_final = vector_final / np.sum(vector_final)
    print('层次权重：{0}'.format(one_final.tolist()))
    print()
    # print('最大特征值为：{0}\n对应的特征向量：\n{1}\n特征归一化权重值：{2}'.format(lamda_max, vector_final, one_final))
    return around(one_final, 4).tolist()


# 熵权化
# 定义熵值法函数
def entropy_weight(args):
    data_array = array(args['data'])
    print("data_array: ", data_array)

    '''熵值法计算变量的权重'''
    # 行列转换
    x = data_array.T
    '''
    如果数据实际不为零，则赋予最小值
    if x==0:
        x=0.00001
    else:
        pass
    '''
    # 求k
    rows = x.shape[0]  # 行
    cols = x.shape[1]  # 列
    if rows == cols == 1:
        return [1]
    k = 1.0 / math.log(rows)
    print("x: ", x)
    # 矩阵计算--
    # 信息熵
    x = array(x)
    lnf = [[None] * cols for i in range(rows)]
    lnf = array(lnf)
    for i in range(0, rows):
        for j in range(0, cols):
            if x[i][j] == None or (x[j] == None).any():
                lnfij = 0.0
            else:
                print("x[i][j]: ", x[i][j])
                print("x[i]: ", x[i])
                # if (x[j] == None).any():
                #     lnfij = 0.0
                if (x[j] < 0).any() or x[i][j] <= 0:
                    lnfij = 0.0
                else:
                    p = x[i][j] / x.sum(axis=0)[j]
                    lnfij = math.log(p) * p
                    print("lnfij: ", lnfij)
            lnf[i][j] = lnfij
    E = lnf
    print("lnf: ", lnf)
    # 将nan空值转换为0
    ej = -k * (E.sum(axis=0))
    # 计算每种指标的信息熵
    d = (1 - ej) / np.sum(1 - ej)
    # 计算冗余度
    # d = 1 - E.sum(axis=0)
    print("d: ", d)
    # 计算各指标的权重
    w = [[None] * 1 for i in range(cols)]
    for j in range(0, cols):
        wj = d[j] / sum(d)
        w[j] = round(wj, 4)
        # 计算各样本的综合得分,用最原始的数据
    print('熵权法权重：{0}'.format(w))
    return w


# 组合常权重
def combination_weight(args):
    data_array = array(args['data'])
    # 行列转换
    x = data_array.T
    # 层次权重
    hierarchyData = x[0]
    # 熵权重
    entropyData = x[1]
    # hierarchyData = array(args['hierarchyData'])
    # entropyData = array(args['entropyData'])
    # 权重排序
    weight_sort = hierarchyData[np.argsort(hierarchyData)]
    print("weight_sort:", weight_sort)
    n = np.size(weight_sort)
    p = 0
    for i in range(n):
        p += (i + 1) * weight_sort[i]
    print("p:", p)
    # 线性系数
    a = 1
    if n != 1:
        a = round(2 / (n - 1) * p - (n + 1) / (n - 1), 4)
    print('线性系数：{0}'.format(a))
    combination_data = hierarchyData * a + entropyData * (1 - a)
    print('组合常权重：{0}'.format(combination_data))
    return around(combination_data, 4).tolist()


# 变权权重(权重，均衡系数)
def variable_weight(args):
    data_array = array(args['data'])
    # 行列转换
    x = data_array.T
    # 权重
    weight = x[0]
    # 均衡系数
    equalization = x[1]
    # weight = array(args['weight'])
    # equalization = array(args['equalization'])
    n = np.size(weight)
    w_weight = []
    for i in range(n):
        p = 0
        for j in range(n):
            p += equalization[j] * weight[j]
        w_weight.append(around(p, 4))
    print('变权商：{0}'.format(w_weight))
    # 变权权重
    x = []
    for i in range(n):
        x.append(around(equalization[i] * weight[i] / w_weight[i], 4))
    print('变权权重：{0}'.format(x))
    # print(x.sum)
    return x


# [0.1928, 0.4692, 0.2657, 0.0723]

# 指标均衡系数
def indicator_equilibrium(args):
    data_array = array(args['data_array'])
    print(data_array)
    k = array(args['k'])
    rows = data_array.shape[0]
    coefficient_list = []
    for i in range(0, rows):
        # 指标数据（最小阈值，最大阈值，标准值，测量值,报警值）
        coefficient = equilibrium_coefficient(data_array[i][0], data_array[i][1], data_array[i][2], data_array[i][3], k)
        # print('指标测量数据：{0}----{1}'.format(data_array[i], health))
        coefficient_list.append(round(coefficient, 4))
    print('指标均衡系数向量：{0}'.format(coefficient_list))
    return coefficient_list


# 均衡系数(最小值、最大值、惩戒阈值、测量值、系数)
def equilibrium_coefficient(min_data, max_data, threshold, data, k):
    if (min_data == None or max_data == None or threshold == None or data == None):
        return 1
    else:
        return round(math.exp(abs((data - threshold) / (max_data - min_data)) * k), 4)


# 健康度计算
def health_calculation(weight, health_data):
    n = np.size(weight)
    p = 0
    for i in range(n):
        p += weight[i] * health_data[i]
    print('健康度：{0}'.format(p))
    return round(p, 4)


# 白化权函数
def gray_cloud_cluster(args):
    health_data = array(args['data'])
    weight = array(args['weight'])
    n = np.size(health_data)
    # 聚类系数向量
    health_cluster = []
    # 白化权值
    whitening_weight = []
    for i in range(n):
        x = health_data[i]
        x_health = []
        if 0 <= x <= 0.3:
            x_health.append(math.exp(pow(x, 2) / (2 * pow(0.1, 2))))
        else:
            x_health.append(0)
        if 0.1 <= x <= 0.5:
            x_health.append(math.exp(pow((x - 0.3), 2) / (2 * pow(0.067, 2))))
        else:
            x_health.append(0)
        if 0.3 <= x <= 0.7:
            x_health.append(math.exp(pow((x - 0.5), 2) / (2 * pow(0.067, 2))))
        else:
            x_health.append(0)
        if 0.5 <= x <= 0.9:
            x_health.append(math.exp(pow((x - 0.7), 2) / (2 * pow(0.067, 2))))
        else:
            x_health.append(0)
        if 0.7 <= x <= 1.0:
            x_health.append(math.exp(pow((x - 1.0), 2) / (2 * pow(0.1, 2))))
        else:
            x_health.append(0)
        whitening_weight.append(x_health)
    whitening_weight = np.array(whitening_weight)
    print('白化权值：{0}'.format(whitening_weight))

    rows = whitening_weight.shape[0]  # 行
    cols = whitening_weight.shape[1]  # 列
    for j in range(0, cols):
        data = 0
        for i in range(0, rows):
            data += whitening_weight[i][j] * weight[i]
        health_cluster.append(data)
    # health_cluster= whitening_weight*weight
    print('聚类系数向量：{0}'.format(health_cluster))
    return health_cluster


# 向量归一化
def vector_normalization(args):
    data = array(args['data'])
    var = np.mat(data)
    # 创建向量集合
    res = np.zeros_like(var)
    norm = np.sum(var)
    for i in range(var.shape[0]):
        for j in range(var.shape[1]):
            res[i, j] = var[i, j] / norm
    print('归一化向量：{0}'.format(res))
    return res.tolist()


# index_data3 = {"data": [[0.3209, 0.3209, 0.3209], [0.4928, 0.4928, 0.4928], [0.8597, 0.8597, 0.8597]]}
# index_data3 = {"data": [[0.9288,0.9743, 0.8543], [0.9333, 0.9000, 0.7333], [0.8800, 0.8400, 0.8000]]}
# index_data3 = {"data": [[0.5396, 0.1924], [0.2970, 0.7077], [0.1634, 0.0999]]}
# # (0.5396, 0.2970, 0.1634)
# print(combination_weight(index_data3))
#(最小阈值，最大阈值，标准值，测量值,报警值,指标类型）
index_data3 ={"data":[[0.8324,0.8324,0.8324],[0.9857,0.9857,0.9857]]}
entropy_weight(index_data3)