【机器学习】支持向量机基础认识与详细实战案例

---

前言

本文将详细介绍Python中支持向量机的原理、参数详解、模块使用和实例。
对于原理部分只会简单解释，网上有许多详细原理教程，可以自行搜索本文主要是实践操作

一、支持向量机是什么？

支持向量机（Support Vector Machine, SVM）是一种常用的分类与回归算法，广泛应用于数据挖掘、图像识别、自然语言处理等领域。Python是目前非常流行的编程语言之一，其强大的科学计算和机器学习库使得Python成为SVM的一种优秀实现语言。

二、原理

SVM的基本思想是找到一个最优的超平面，将不同类别的数据分开。超平面可以是任意维度的，但在二维空间中，它就是一条直线，可以通过以下公式表示：

wTx+b=0

其中，$w$是法向量，$x$是数据点，$b$是偏移量。

在二分类问题中，假设有两个类别：1和-1。我们要找到一个最优的超平面，使得所有属于类别1的数据点在超平面的一侧，所有属于类别-1的数据点在超平面的另一侧。超平面与两个最近的数据点之间的距离被称为间隔。最优的超平面是间隔最大的超平面。

间隔的计算公式如下：

其中，$x_i$是数据点，$||w||$是法向量的模长。

三、参数解释

SVM有多个参数需要调整，以下是常见的参数：

C：惩罚参数，用于平衡模型的准确率和过拟合风险。C越大，模型的准确率越高，但也会增加过拟合的风险。默认值为1。

kernel：核函数，用于将数据从低维度空间映射到高维度空间。常见的核函数有线性核函数、多项式核函数和高斯核函数等。

gamma：核函数的系数，用于控制映射后的样本分布。gamma越大，映射后的分布越集中，决策边界也越复杂。

degree：多项式核函数的阶数，用于控制映射后的维度。degree越高，映射后的维度越高，模型也会更加复杂。

coef0：核函数的常数项，用于调整核函数的形状。

下面是一些常见的SVM模型返回方法：

support_vectors_: 返回支持向量的数组。支持向量是在训练模型时最关键的数据点，它们决定了模型的决策边界。

coef_: 返回线性SVM模型的权重向量。权重向量可以用于分析数据集中哪些特征最相关，以及它们对模型的影响程度。

intercept_: 返回SVM模型的截距项。截距项是决策边界的偏移量，它在计算预测值时起到关键作用。

dual_coef_: 返回非线性SVM模型的拉格朗日乘子。拉格朗日乘子是非线性SVM算法中的重要参数，它用于计算核函数的权重。

n_support_: 返回每个类别的支持向量数量。这个值可以帮助我们评估模型的复杂度和泛化能力。

decision_function(X): 返回决策函数值，即SVM模型对输入数据集X的预测值。决策函数值可以用于评估模型的性能，以及生成ROC曲线和AUC值。

predict(X): 返回SVM模型对输入数据集X的分类预测结果。这个方法用于实际应用中对新数据进行分类。

score(X, y): 返回SVM模型在数据集(X, y)上的准确率。这个方法用于评估模型在训练集和测试集上的性能，以及确定模型的最佳参数设置。

四、实战案例

1.最大边缘分离超平面

在向量机中，最大边缘分离超平面是一条平面或超平面，它能够将不同类别的数据点正确分开，并且使得不同类别之间的边际（margin）最大化。这个超平面在分类问题中起到关键作用，因为它可以用来做新数据点的预测，也可以帮助我们更好地理解数据的结构。
在二维平面上，最大边际分离超平面就是一条直线。但是，在高维空间中，最大边际分离超平面是一个超平面。对于一个二分类问题，我们可以定义超平面方程为：

• w^T x + b = 0

其中，w 是一个向量，x 是输入特征向量，b 是偏差（也称为截距）。所有满足此方程的点都位于超平面上，w 是法向量，决定了超平面的方向。偏差 b 确定了超平面与原点之间的距离。
在训练过程中，我们希望找到一个超平面，使得它能够正确地分类训练数据，并且使得不同类别之间的距离最大化。这个距离就是边际（margin），它由超平面与离它最近的数据点构成。这些数据点被称为支持向量（support vectors），因为它们对模型的构建和预测起到了重要作用。
因为 SVM 本质上是一个优化问题，我们需要定义一个目标函数来最小化错误率，并最大化边际。通常我们使用软间隔 SVM 来解决非线性可分问题，这时目标函数将包括一个惩罚项，来允许一些数据点位于边际内部。SVM 的优化问题可以通过二次规划（Quadratic Programming）来解决。
最终，SVM 会找到一个最大边际分离超平面，并根据训练数据的特点来确定 w 和 b 的值。这个超平面可以被用于新数据点的分类，并可以帮助我们更好地理解数据结构。

• 生成数据
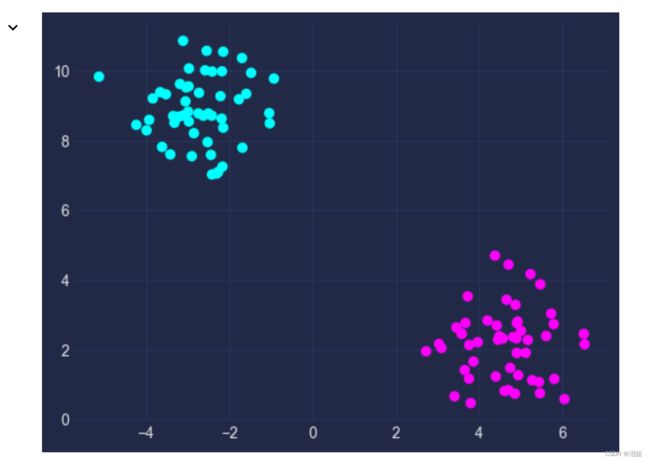
  这里我们生成一个二分类的数据

from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from sklearn.inspection import DecisionBoundaryDisplay
import matplotlib.pyplot as plt
import mplcyberpunk
plt.style.use('cyberpunk')
#%%
X,y=make_blobs(n_samples=100,centers=2,random_state=42)
plt.scatter(X[:,0],X[:,1],c=y)

• 模型训练，构建最大边缘分离超平面
  这里我们采用4组不同（C，gamma)参数进行模型的训练，观察模型的不同效果

labeles=[
    (1000,0.01),(1,0.01),(1000,0.1),(1,0.1)
]

n=1
for c,gamra in labeles:
    ax=plt.subplot(220+n)
    n+=1
    clf=SVC(C=c,gamma=gamra,kernel='linear',random_state=42)
    clf.fit(X,y)
    plt.scatter(X[:,0],X[:,1],c=y)
    DecisionBoundaryDisplay.from_estimator(
    clf,
    X,
    plot_method="contour",
    colors="k",
    levels=[-1, 0, 1],
    alpha=0.5,
    linestyles=["--", "-", "--"],
    ax=ax,
)
    plt.scatter(clf.support_vectors_[:, 0],clf.support_vectors_[:, 1],
        s=100,
        linewidth=1,

        facecolors="none",
        edgecolors="r")

    plt.title(f'C:{c},gamma:{gamra}')

plt.show()

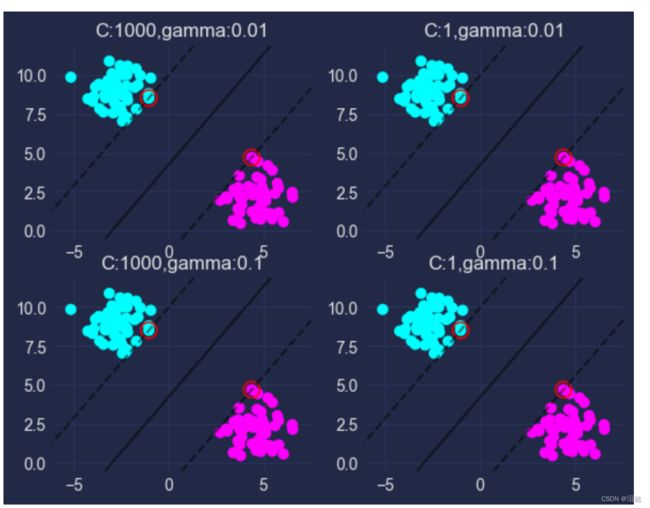
我们可以观察到支持向量点构建出的最大边缘分离超平面将两者分成两类，但由于改数据集较简单，不容易观察出参数不同对模型的效果影响，我们可以用iris数据集来展示看一下，这里我们为了简单运算，所以只选择两个类别

from sklearn.datasets import load_iris
iris=load_iris()
X=iris.data[:,2:4]
y=iris.target
label=(y==0)|(y==1)
X=X[label]
y=y[label]



labeles=[
    (1000,0.01),(1,0.01),(1000,0.1),(1,0.1)
]

n=1
for c,gamra in labeles:
    ax=plt.subplot(220+n)
    n+=1
    clf=SVC(C=c,gamma=gamra,kernel='linear',random_state=42)
    clf.fit(X,y)
    plt.scatter(X[:,0],X[:,1],c=y)
    DecisionBoundaryDisplay.from_estimator(
    clf,
    X,
    plot_method="contour",
    colors="k",
    levels=[-1, 0, 1],
    alpha=0.5,
    linestyles=["--", "-", "--"],
    ax=ax,
)
    plt.scatter(clf.support_vectors_[:, 0],clf.support_vectors_[:, 1],
        s=100,
        linewidth=1,

        facecolors="none",
        edgecolors="r")

    plt.title(f'C:{c},gamma:{gamra}')

plt.show()

通过比较观察到，当c比较大时候，最大边缘分离超平面比较小，随然较大的C可以提高模型准确率，但也会提高拟合风险，这里我们引入软间隔的概念

2.软间隔

软间隔是SVM中的一种改进方法，它允许在一定程度上容忍一些噪声或异常点。在传统的硬间隔SVM中，如果数据集不是线性可分的，那么模型将无法找到一个完美的决策边界。而软间隔SVM则允许一些数据点跨越到决策边界的另一侧，从而更好地适应非线性可分的数据集。

软间隔SVM通过引入一个松弛变量$\xi$来实现。在软间隔SVM中，目标函数不再要求决策边界能够完全分离正负样本，而是希望能够在容忍一定的误差的情况下找到一个最优的决策边界。具体来说，目标函数可以表示为：

min⁡w,b,ξ12∥w∥2+C∑i=1mξiw,b,ξmin​21​∥w∥2+C∑i=1m​ξi​

其中，${\xi }_i$表示第$i$个样本点距离正确分类决策边界的距离，$C$是一个惩罚因子，用于平衡最小化间隔和最小化误差的权重。当$C$较大时，模型将更加注重最小化误差，从而得到更复杂的决策边界；当$C$较小时，模型更加注重最小化间隔，从而得到更简单的决策边界。这里的松弛变量$\xi$的引入允许一些样本点被误分类或者位于决策边界上方或下方，但是它们对目标函数的贡献会被惩罚项$C{\sum }_{i=1}^m{\xi }_i$所抵消。

软间隔SVM可以通过调整惩罚因子$C$来控制模型的复杂度和泛化能力。当$C$取值较大时，模型的准确率可能会有所提高，但是泛化能力可能会受到影响；当$C$取值较小时，模型的泛化能力会更好，但是准确率可能会降低。因此，在实际应用中，需要根据具体的数据集和问题来调整惩罚因子$C$的取值。

总之，软间隔SVM是一种强大的机器学习算法，可以在处理非线性可分数据集时取得很好的效果。它通过引入松弛变量和惩罚项来平衡最小化间隔和最小化误差的权重，从而得到更加鲁棒的决策

简单的说，软间隔为了避免模型过于追求准确率，而提高模型决策边界的复杂程度，正常情况下一般我们选择较小的C惩罚项

3. 非线性分类问题和核函数

在面对非线性分类问题时，传统的支持向量机分类器无法有效处理。这时，可以使用核函数来将非线性分类问题映射到高维空间中，从而在高维空间中进行线性分类。具体来说，核函数将原始空间中的数据点映射到一个更高维度的特征空间，使得原始空间中的非线性问题在特征空间中变成线性可分的问题。在特征空间中，可以使用线性分类器，如SVM分类器来进行分类。

常用的核函数有以下几种：

• 线性核函数：$K(x_i,x_j)=x_i^T{x}_j$
• 多项式核函数：$K(x_i,x_j)=(x_i^T{x}_j+r{)}^d$，其中r为常数，d为多项式的阶数。
• RBF核函数：$K(x_i,x_j)=e^{-\gamma ||x_i-x_j|{|}^2}$，其中$\gamma$为正常数，$||x_i-x_j||$为欧氏距离。
• Sigmoid核函数：$K(x_i,x_j)=tanh(\alpha x_i^T{x}_j+c)$，其中$\alpha$和$c$为常数。

这些核函数可以在sklearn库中的SVM分类器中使用。SVM分类器的构造函数有一个kernel参数，可以用于指定使用的核函数类型。例如，可以使用RBF核函数来构造一个非线性分类器：

from sklearn.svm import SVC

clf = SVC(kernel='rbf')

需要注意的是，使用核函数会增加计算复杂度，因为映射到高维特征空间后，数据点的维度会变得非常高。因此，在实际应用中，需要根据具体情况选择适当的核函数和参数来平衡计算复杂度和分类精度。

介绍一个使用高斯核函数实例

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm

xx, yy = np.meshgrid(np.linspace(-3, 3, 500), np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
Y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)

# fit the model
clf = SVC(gamma="auto",kernel='rbf')
clf.fit(X, Y)

# plot the decision function for each datapoint on the grid
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.imshow(
    Z,
    interpolation="nearest",
    extent=(xx.min(), xx.max(), yy.min(), yy.max()),
    aspect="auto",
    origin="lower",
    cmap=plt.cm.PuOr_r,
)
contours = plt.contour(xx, yy, Z, levels=[0], linewidths=2, linestyles="dashed")
plt.scatter(X[:, 0], X[:, 1], s=30, c=Y, cmap=plt.cm.Paired, edgecolors="k")
plt.xticks(())
plt.yticks(())
plt.axis([-3, 3, -3, 3])
plt.show()

使用具有RBF核的非线性SVC执行二进制分类。要预测的目标是对输入进行异或运算。颜色深度是指决策分数，越到中心，颜色越深

4.不同核函数效果

• 数据集加载

from sklearn import svm
from sklearn.inspection import DecisionBoundaryDisplay
iris=load_iris()
X=iris.data[:,2:4]
y=iris.target

• 模型训练构建
  这里我们采用不同的核函数模型:
• svm.SVC(kernel=“linear”, C=C)：线性SVM模型，使用线性核函数。
• svm.LinearSVC(C=C, max_iter=10000)：线性SVM模型，同样使用线性核函数。与svm.SVC不同的是，LinearSVC是基于liblinear库实现的，它采用了不同的优化算法，可以更快地收敛。max_iter是最大迭代次数，用于指定算法的停止条件。
• svm.SVC(kernel=“rbf”, gamma=0.7, C=C)：非线性SVM模型，使用径向基核函数（RBF）。gamma是核函数的系数，用于控制决策边界的形状。
• svm.SVC(kernel=“poly”, degree=3, gamma=“auto”, C=C)：非线性SVM模型，使用多项式核函数。degree是多项式的阶数，gamma是核函数的系数，

models = (
    svm.SVC(kernel="linear", C=C),
    svm.LinearSVC(C=C, max_iter=10000),
    svm.SVC(kernel="rbf", gamma=0.7, C=C),
    svm.SVC(kernel="poly", degree=3, gamma="auto", C=C),
)
models = (clf.fit(X, y) for clf in models)

• 构造决策边界可视化

# title for the plots
titles = (
    "SVC with linear kernel",
    "LinearSVC (linear kernel)",
    "SVC with RBF kernel",
    "SVC with polynomial (degree 3) kernel",
)

# Set-up 2x2 grid for plotting.
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)

X0, X1 = X[:, 0], X[:, 1]


for clf, title, ax in zip(models, titles, sub.flatten()):
    disp = DecisionBoundaryDisplay.from_estimator(
        clf,
        X,
        response_method="predict",
        cmap=plt.cm.coolwarm,
        alpha=0.8,
        ax=ax,
        xlabel=iris.feature_names[0],
        ylabel=iris.feature_names[1],
    )
    ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors="k")
    ax.set_xticks(())
    ax.set_yticks(())
    ax.set_title(title)

plt.show()

可以发现线性核函数的决策边界为折线，适用于线性分类问题，而rbf和poly核函数，决策线就相对圆滑，适用于非线性数据。

5.回归问题

向量机除了用于分类问题之外，还可以应用于回归问题。在回归问题中，我们希望根据一组输入特征来预测一个连续的输出值。与分类问题不同，回归问题需要预测连续的值，因此我们需要另一种方法来构建模型。

在支持向量机回归中，我们首先确定一个边界（或称为管道），该边界由两个平行的超平面构成。这些平面被放置在离数据点最远的位置，这些数据点称为支持向量。这条边界被称为 ε - 管道，其中 ε 是管道的宽度。管道中的任何数据点都被认为是正确预测，而位于管道之外的点则被认为是错误预测。

与分类问题类似，我们的目标是最小化误差，同时保持最大的边界。误差定义为实际输出值与模型预测值之间的差异。在回归问题中，我们需要找到一个函数 f(x)，将输入 x 映射到输出 y。

与分类问题不同的是，我们在回归问题中可以使用不同的损失函数，如平方误差、绝对误差或 Huber 损失。这些损失函数可以根据具体问题来选择。

在支持向量机回归中，我们使用核函数来扩展模型以处理非线性回归问题。RBF 和多项式核函数也可以用于回归问题中。我们可以在实现时使用 Scikit-learn 库中的 SVR（支持向量机回归）模型来完成回归问题的建模和预测。

• 构建数据集

from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from sklearn.inspection import DecisionBoundaryDisplay
import matplotlib.pyplot as plt
import mplcyberpunk
plt.style.use('cyberpunk')
import numpy as np


X = np.sort(5 * np.random.rand(100, 1), axis=0)
y = np.sin(X).ravel()

#增添点噪音
y[::10] += 3 * (0.5 - np.random.rand(10))


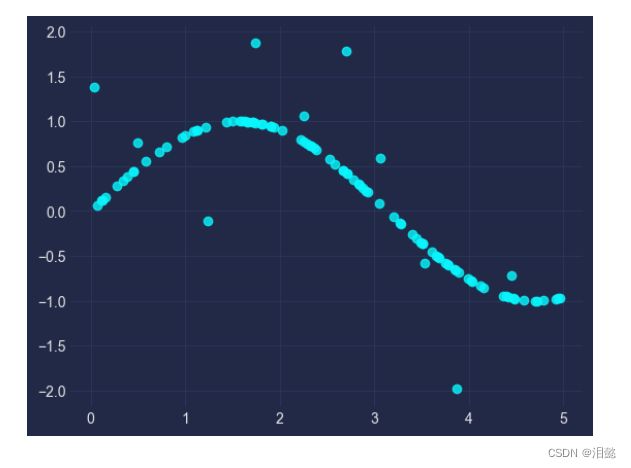
plt.scatter(X,y,alpha=0.8)

• 模型构建
  这里我们依旧构建不同的核函数模型观察效果，
  分别构建rbf,linear,poly核函数模型

from sklearn.svm import SVR
svr_rbf=SVR(kernel='rbf',C=1,gamma=0.1,epsilon=0.1)
svr_lin = SVR(kernel="linear", C=1, gamma="auto")
svr_poly = SVR(kernel="poly", C=1, gamma="auto", degree=3, epsilon=0.1, coef0=1)

• 模型训练可视化比较

lw = 2

svrs = [svr_rbf, svr_lin, svr_poly]
kernel_label = ["RBF", "Linear", "Polynomial"]
model_color = ["m", "c", "g"]

fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(8, 6), sharey=True)
for ix, svr in enumerate(svrs):
    axes[ix].plot(
        X,
        svr.fit(X, y).predict(X),
        color=model_color[ix],
        lw=lw,
        label="{} model".format(kernel_label[ix]),
    )
    axes[ix].scatter(
        X[svr.support_],
        y[svr.support_],
        facecolor="none",
        edgecolor=model_color[ix],
        s=50,
        label="{} support vectors".format(kernel_label[ix]),
    )
    axes[ix].scatter(
        X[np.setdiff1d(np.arange(len(X)), svr.support_)],
        y[np.setdiff1d(np.arange(len(X)), svr.support_)],
        facecolor="none",
        edgecolor="k",
        s=50,
        label="other training data",
    )
    axes[ix].legend(
        loc="upper center",
        bbox_to_anchor=(0.5, 1.1),
        ncol=1,
        fancybox=True,
        shadow=True,
    )

fig.text(0.5, 0.04, "data", ha="center", va="center")
fig.text(0.06, 0.5, "target", ha="center", va="center", rotation="vertical")
fig.suptitle("Support Vector Regression", fontsize=14)
plt.show()

可以发现，在回归问题中选择RBF和ploy核函数能够很好的拟合非线性函数，而linear核函数在线性数据中更占优势

总结，

本文介绍了SVM的原理、参数详解、Python模块的使用以及实例。SVM是一种常用的监督学习算法，可以用于分类和回归问题。通过调整参数，可以优化模型的准确率和泛化能力。在Python中，可以使用sklearn.svm和libsvm模块来实现SVM算法。

• 上述有任何错误的地方欢迎指正
  希望大家多多支持，后续分享更多有趣的东西