递归的深层次理解+初始搜索算法

1)什么是递归:就是函数自己调用自己的过程

2)为什么会使用到递归:主问题->相同的子问题，相同的子问题->一样相同的子问题

3)递归结束的条件:也就是细节和出口最小的不能在继续进行分割的子问题

4)宏观看待递归的过程:

1)不要在意递归展开的细节图

2)那递归的函数看成是一个黑盒

3)相信这个黑盒一定可以完成这个任务

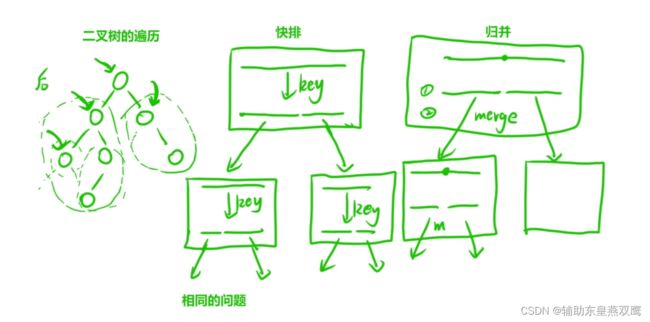
3.1)进行二叉树遍历的这个函数就是来针对于当前根节点进行后续遍历的，相信这个函数一定是可以完成二叉树的后续遍历的，进行写代码的时候，不要过多的考虑这个函数实现的内部细节，当成一个黑盒，先进行遍历根节点，再进行遍历左子树和右子树；

针对于二叉树的后序遍历来说先进行遍历根节点，在进行遍历这棵树的左子树和右子树；

void dfs(Node* root){
//注意递归结束的条件,是划分这个子问题的最小单元,也就是递归到叶子节点
 if(root==null) return null;
  dfs(root.left);//遍历这棵树的左子树
  dfs(root.right);//遍历这棵树的右子树
  printf(root.val);//打印根节点
}

3.2)针对于快排上来说，这个函数是让指定的数组的给定区间区间有序，参数是(传入数组，传入左边的区间，在传入右边的区间)，目的是让左边的区间到右边的区间有序；

具体的步骤是先找到中间节点，划分出一个区间，先让左边的区间(从开始位置到基准值)有序，再让右边的区间(从基准值到右边的区间)有序，而这个让左区间有序和右区间有序，正好是我们所写的这个函数的任务(让数组的某一段区间有序)，这样就划分除了子问题，还是要把这个我们自己所写的函数看成是一个黑盒，并且相信这个黑盒一定可以完成这个任务；

之前学过快排，让左段区间有序，还要从左段区间中找出一个基准值，继续进行划分

让右端区间有序，就需要从右端区间找出一个基准值，在进行继续划分，不断地进行子问题的划分；

void quicksort(int left,int right,int[] array){//这个函数的目的就是为了让数组的某一段区间有序
   if(left>=right)//划分子问题的最小区间,只有一个元素,本身就是有序的
int privot=getPrivot(left,right,array);
quicksort(left,privot,array);//让左区间有序
//这个函数就是为了让这个数组的某一段区间有序,此时我们是让这个数组的left到privot区间是有序的,我们相信这个函数一定可以完成这个任务,并且把这个函数看作是一个黑盒
quicksort(privot+1,right,array);//让右区间有序;

3.3)针对于归并排序来说，我们写一个函数实现归并排序，这个函数的目的就是为了实现归并排序，也就是让数组的某一段区间有序，整体思路就是先划分数组的中间元素，从左端点到中间元素排序的，从中间元素到右端点排序的，左区间有序，有区间有序，那么在整体合并两个有序数组即可，终止条件就是数组没有元素或者只有一个元素；

   void merage(int left,int right,int[] array){//这个函数的目的就是为了让数组的某一段区间有序
        if(left>=right) return ;
        int mid=(left+right)/2;
        merage(left,mid,array);//先进行归并排序左区间
        merage(mid+1,right,array);//再进行归并排序右区间
        sort(left,right,array);//先让左区间有序,再让右区间有序,在整体上进行排序)
}

5)如何写好递归

5.1)先找到相同的子问题，函数头的参数的传递和某一个子问题是一模一样的，归并排序的子问题就是给定数组的一段区间，把数组进行排一下序就可以了，二叉树的后续遍历是，跟定根节点进行后续遍历，正好适合函数头的功能是一模一样的；

5.2)只关心某一个子问题是如何解决了，这就涉及到了函数体的书写

5.3)避免写出死递归，写出口的时候，只关心子问题到那里的时候是不可以进行分割了，接下里就来看将数据结构中二叉树的题，在使用宏观方式理解一下

搜索:就是为了查找值

1)前面是深度优先遍历，后面是宽度优先遍历

2)遍历只是一种形式，目的是为了搜索，搜索是为了把所有的情况列举出来的时候，有可能是一个树状的形式，有可能是一个图状的形式，把所有的情况都给进行暴力的遍历一遍的时候，其实就是一个搜索，暴力枚举所有的结果，把所有可能出现的情况都给遍历一遍；

搜索=dfs(深度优先遍历和递归有关)+bfs(宽度优先遍历)

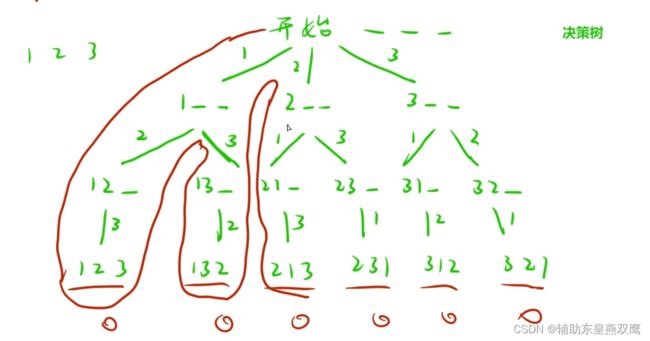
拿出最经典的问题，全排列问题:题目就是类似于说，有1 2 3三个数，总共可以排列出多少种不同的情况:第一个格子放1......高中的排列组合问题；

通过深度优先搜索就可以进行遍历所有的排序序列，也可以用宽度优先遍历来进行遍历所有的情况，把每一层的结果存放到一个队列里面

就比如说我再进行深度优先遍历的时候，找到了123所在的位置，但是此时并没有找到我所想要的数，此时就回退到1号位置即可，所以说深搜的时候是一定会涉及到回溯的，因为在进行深搜的过程中是一定会回退到上一级的，你返回到上一层的时候实际上就是一个回溯

回溯与减枝 

1)回溯:就是深度优先遍历，就是再进行尝试某一种结果的时候，在进行寻找解决问题的某一种情况的时候，发现某一种情况行不通，行不通的时候，于是就返回退回到上一级，从上一级继续开始尝试；

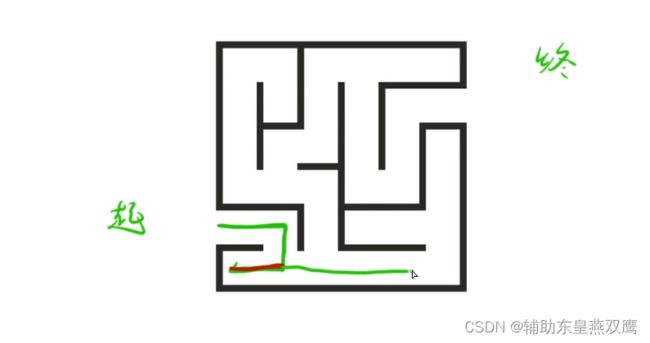
2)以走迷宫的例子来进行理解一下:假设当前从起点出发，只要是有拐点，就分成两种情况，要么是向左走，要么是向右走，如果向左走，就一直向左走，直接一条路走到黑，如果发现向左侧走走不通的话，就直接返回到那个决策的点，下面中红色的线代表的是回溯 

3)剪枝:在回溯岔路口上有若干种选择，但是我们明确当前要选择的路已经不是我们最终想要的结果，我们就可以将这种结果给剪切掉，这就是剪枝

当我两条路都走过的时候，回溯到园点的时候，此时有两条路可以走，但是这两条路我都已经走过了，而且还发现根本走不通，此时就可以得出结论，这两条路都不用再走了，当出现这两条路都不用再继续走的情况下，就是剪支；

一)汉诺塔:

题目要求:在移动盘子和生成最终结果的过程中，要注意的是大的盘子是不可以罗列在小的盘子上面的

面试题 08.06. 汉诺塔问题 - 力扣（Leetcode）

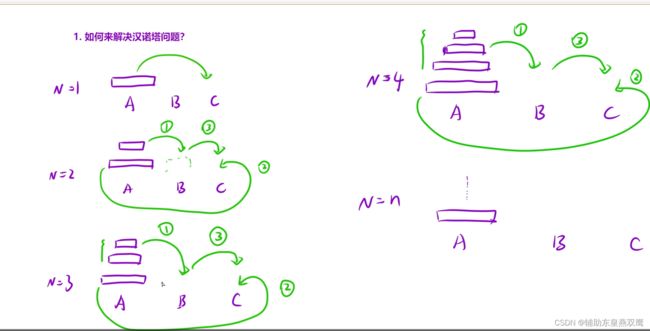
解决汉诺塔问题的根本思路:

1)先把A盘子上面的N-1个盘子借助C盘子移动到B盘子上面，先把A上面的N-1个盘子转移到B上面；

2)把A上面的最大的盘子直接移动到C上面

3)最后再将B上面的N-1个盘子借助C盘子移动到A上

1)当我们解决一个问题的时候发现某一个问题更小的子问题可以使用相同的方式来进行解决的话，此时就可以使用递归来解决

2)当解决一个大问题的时候，又出现了一个相同类型的子问题，解决这个大问题的方式和解决这个子问题的方式是一模一样的，当我们继续解决这个子问题的时候，又发现了相同类型的子问题，此时就可以使用递归地解决，都是从一个位置开始借助另一个位置放到最终的位置上面；

1)重复子问题==函数头

1)上面的重复子问题就是1 2 3步，重复子问题名称:把X柱子上面的一堆盘子，借助y柱子，转移到z柱子上面；

2)void dfs(x，y，z，int n)，你传入N个柱子，我就可以把X上面的N个盘子，借助Y盘子的帮助，转移到Z上面，一开始我们要解决的问题就是要把A上面的个柱子借助B柱子转移到C柱子上；

2)只关心某一个子问题在做什么，设计函数体

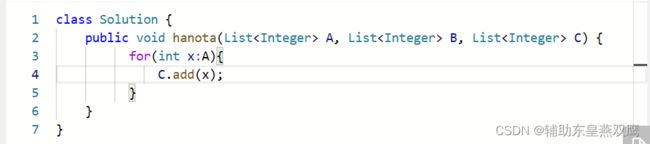
class Solution {
    //主函数是为了将A的N个盘子借助B移动到C上
    public void dfs(List A, List B, List C,int n){
        if(n==1){
            C.add(A.remove(A.size()-1));
            return;
        }else{
dfs(A,C,B,n-1);
//先将A主子上面的N-1个盘子从A借助C移动到B上,和主函数做的事情是相同的
C.add(A.remove(A.size()-1));
//里面的remove函数是一个下标,直接将A剩下的最后一个大盘子移动到C上
dfs(B,A,C,n-1);
//最后将B上面的N-1个盘子从B开始借助A移动到C上面
        }
    }
    public void hanota(List A, List B, List C) {
          dfs(A,B,C,A.size());
    }
}

3)递归的出口:是哪一个子问题不可以再继续划分

要注意，移动的是最小的那个盘子 

当N=1的时候，直接将X的盘子放到Z上面

二)合并两个有序链表:

剑指 Offer 25. 合并两个排序的链表 - 力扣（Leetcode）

在做递归的题的时候一定要找到重复子问题

解题思路:重复子问题+宏观的看待问题

1)重复子问题:函数头的设计:Node dfs(Node node1，Node node2)

把这个函数头当成一个黑盒，相信他一定可以完成这个任务

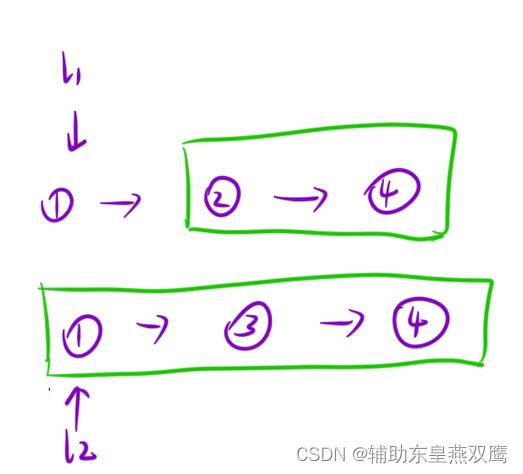
这里面的重复子问题就是合并两个有序链表，当在进行合并两个有序链表的时候，先找到两个链表中最小的节点充当头节点，再继续合并两个有序链表，最终将头节点+后面合并到一起的链表；

2)只是关心某一个问题在做什么:

2.1)首先进行比较两个传入的链表的较小值

2.2)选择较小的值来充当头节点

2.3)让头节点进行连接剩下的两个链表合并的结果，两个链表是如何进行合并的并不关心，只是相信这个函数一定可以帮助我完成这个操作；

2.4)直接返回头节点

3)递归的出口:子问题不能再继续划分if(l1==null)||(l2==null)，谁为空返回另一个

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        //1.找到函数出口
        if(l1==null) return l2;
        else if(l2==null) return l1;
        //先找到两个链表的头结点的较小值
        else if(l1.val>=l2.val){
            l2.next=mergeTwoLists(l1,l2.next);//最小值的节点.next(两个子链表合并起来的节点)
            return l2;
          }
        else {
//把这个函数看成是一个黑盒,并相信这个函数一定可以完成这个任务
          l1.next=mergeTwoLists(l1.next,l2);
          return l1;
        }
    }
}

递归VS循环(迭代)之间的关系:

递归:是否存在重复子问题

循环:也是在不断地重复执行子问题

所以循环和递归是可以相互之间转换的

递归VS深搜之间的关系:

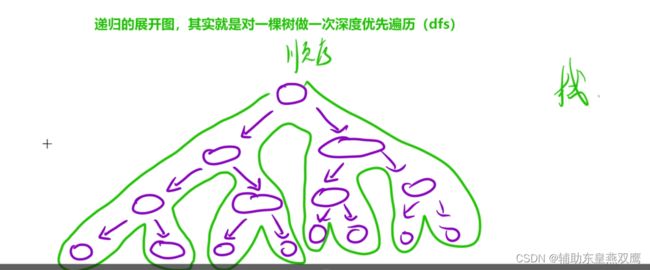
1)递归的展开图和树的优先遍历是一样的，也就是说模拟递归的执行过程其实就是对一棵树做一次深度优先遍历，也被称之为是DFS，递归的展开图，其实就是对一棵树做一次深度优先遍历；

2)例如如果你想要将这个递归转化成循环，你需要借助一个栈来进行帮助，原因就是因为当我们进行递归展开根节点的左子树的时候，当前根节点并没有执行完成，没有执行完的意思是说我还没有展开当前根节点的右子树部分，所以需要用到栈来保存根节点的信息，方便于左子树打印完成之后，能够找到根节点信息，进而去调用右子树，所以就需要栈来保存根节点的信息

3)中序遍历只存在于二叉树中

public class HelloWorld {
    public static void print(int[] array,int i){
        if(i==array.length) return;
        System.out.println(array[i]);
        i++;
        print(array,i);
    }
    public static void main(String[] args) {
        int[] array=new int[]{1,2,3,4,5,6,7,8,9,10};
        print(array,0);
    }
}

先序遍历VS后序遍历: 

1)按照顺序打印是先进行打印数字，然后再打印下一层(递归调用)

2)按照反序打印是先进行打印下一层(递归调用)，等到递归回退到函数上一层的时候再来进行打印数字

三)反转链表:

剑指 Offer II 024. 反转链表 - 力扣（Leetcode）

1)先将当前头节点后面的链表先进行逆置，并且把逆置后的链表头结点返回(如果只是将前两个链表进行逆置，那么根本无法找到第三个节点)

2)让当前节点添加到逆置之后的链表的后面的节点即可

3)这个递归问题的退出入口是当进行遍历到叶子节点或者是尾节点或者是当前节点是空

结束条件:当链表中已经没有节点就可以结束了，这个时候结束循环

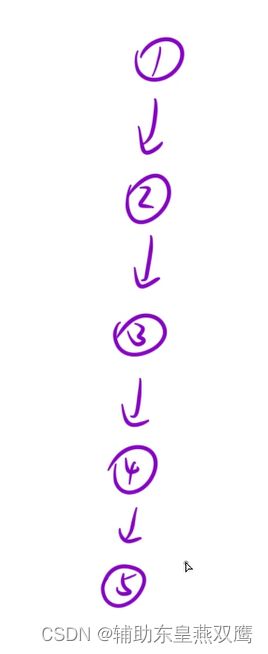
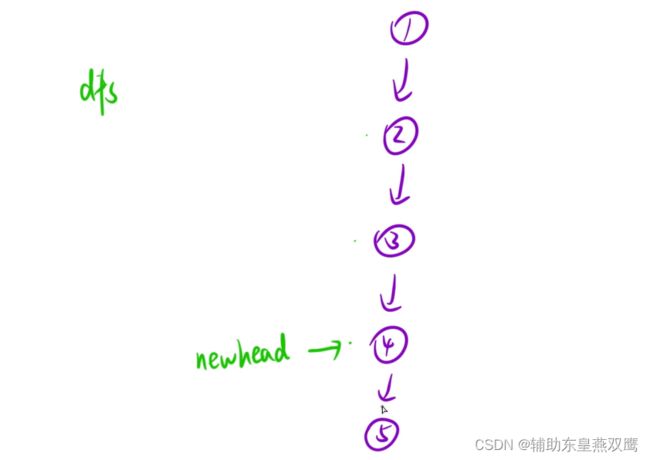
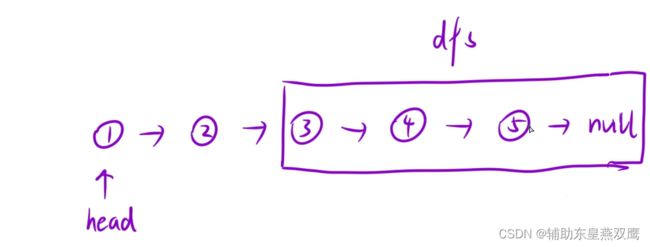
思路:可以将链表看作成是一棵树，其实将下面这个链表做一次后续遍历就可以了，首先有一个dfs函数在不断地进行向下遍历，当遇到空节点或者是叶子节点，此时这个叶子节点就是链表反转之后的头节点，此时在这个函数中将newhead节点进行返回，此时newhead节点是不断返回到上一层；

假设说现在从第5层返回到了第四层，在本层是有能力接收到下层的返回值的(也就是下一层的节点)，将下一个节点的next域指向当前函数的节点，将自己的next置为空，不断向上回退

于是就成功地完成了链表反转的操作；

class Solution {
    public ListNode reverseList(ListNode head) {
//0.当链表中只有一个头结点况且链表为空就不要进行反转了
      if(head==null||head.next==null) return head;
//1.首先将head后面的链表进行翻转,把这个代码看成是一个黑盒并相信这个代码一定可以完成这个任务
       ListNode newHead=reverseList(head.next);
//2.将头节点拼接上去
       head.next.next=head;
//3.头节点要置成null
       head.next=null;
//4.返回新的头节点
       return newHead;
    }
}

其实head.next才是最终的判断条件，newHead在进行向下遍历的过程回退中其实是永远指向的是原链表中的最后一个节点最后向上回退的过程中也是不断地指向链表中的最后一个节点

四)两两交换链表中的节点 

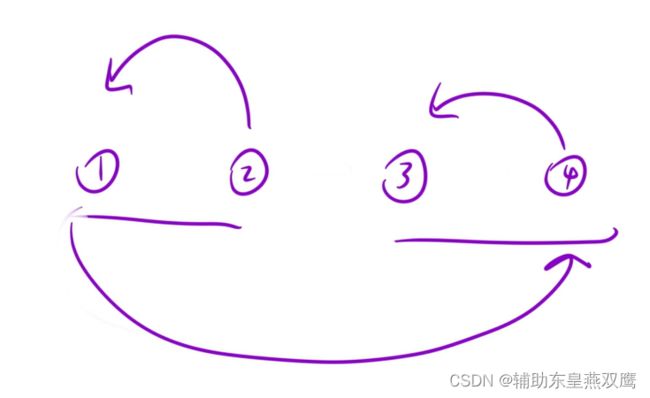
创建一个头节点，我们进行改变的是链表链接的指针，而不是链表中的值来到到交换的目的

class Solution {
    public ListNode swapPairs(ListNode head) {
        if(head==null||head.next==null){
            return head;
        }
       ListNode newHead=new ListNode(0);
       ListNode temp=newHead;
       ListNode front=temp;//辅助循环
       ListNode current=null;
       temp.next=head;//辅助循环
       while(temp.next!=null&&temp.next.next!=null){
           front=front.next;
           current=front.next;   
           temp.next=current;
           front.next=current.next;
           current.next=front;
           temp=front;
       }
       return newHead.next;
    }
}

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {
        if(head==null||head.next==null){
            return head;
        }
       ListNode newHead=new ListNode(0);
       ListNode temp=newHead;
       temp.next=head;//辅助循环
       while(temp.next!=null&&temp.next.next!=null){
           ListNode front=temp.next;
           ListNode current=front.next;   
           temp.next=current;
           front.next=current.next;
           current.next=front;
           temp=front;
       }
       return newHead.next;
    }
}

 

class Solution {
    public ListNode swapPairs(ListNode head) {
        if(head==null||head.next==null){
            return head;
        }
//1.先将第一个节点和第二个节点以后的链表进行逆置把这个函数看作是一个黑盒,并相信这个黑盒一定可以完成这个任务
      ListNode newHead=swapPairs(head.next.next);
      ListNode front=head;
      ListNode current=front.next;
//2.再进行翻转第一个节点和第二个节点
      current.next=front;
      front.next=newHead;
      return current;
    }
}

 1

想要求出3^16次方，只需要求出(3^8)*(3^8)即可，而想要求出3^8只需要求出3^4*3^4即可，1)所以说这里面的子问题就是pow(X，N)就需要求出POW(X，N/2)*POW(X，N/2)即可

2)假设我们此时求的是3^21，那么只需要求出POW(X，N/2)*POW(X，N/2)*X即可

3)先进行编写函数头(也就是子问题):就是int temp=POW(X，N/2)

4)函数体的编写就是:temp*temp或者是temp*temp*x;

lass Solution {
    public double myPow(double x, int n) {
       return n>=0?pow(x,n):1.0/pow(x,(long)(-n));
    }
  public double pow(double x,long n){
       if(n==0){
            return 1.0;
        }
    double temp=pow(x,n/2);
    if(n%2==0) return temp*temp;
    return temp*temp*x; 
  }
}