Pytorch深度强化学习1-3：策略评估与贝尔曼期望方程详细推导

0 专栏介绍

本专栏重点介绍强化学习技术的数学原理，并且采用Pytorch框架对常见的强化学习算法、案例进行实现，帮助读者理解并快速上手开发。同时，辅以各种机器学习、数据处理技术，扩充人工智能的底层知识。

详情：《Pytorch深度强化学习》

---

1 从一个例子出发

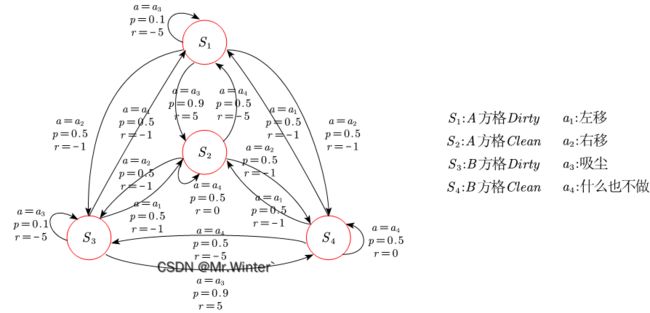
例1：如图所示的真空吸尘器世界只有两个地点：方格A和B。假设吸尘器Agent的传感器可以感知自身处于哪个方格中，以及方格中是否有灰尘；它具有且仅具有左移、右移、吸尘或什么也不做四种行为；假设吸尘器Agent采用的策略是若当前所在地点有灰尘则进行清洁，否则往另一个地点运动。请用马尔科夫决策过程表示吸尘器问题

如图所示即为例1的一种马尔科夫决策过程，其设计思路是：只要采取移动就会造成一定的损失，在有灰尘的方格中若智能体不采取吸尘则会造成严重的损失。朴素地，最优策略在当前方格有灰尘时选择“吸尘”直至清扫干净，在当前方格无灰尘时选择“移动”进行巡查或“什么也不做”节省能源

那么问题来了，智能体要如何决策才能使其长期运行下去得到的奖励最多呢？ 这就是本文要讨论的策略评估问题

2 回报与奖赏

强化学习的目标是找到一个策略

$$\pi \left(s,a\right)=P\left(\mathrm{action}=a|\mathrm{state}=s\right)$$

使智能体长期执行该策略后得到的回报(Return)最大化。自然地，需要定义回报与策略评估的计算方法。引入回报函数：

• $T$步回报函数

$$R_t=\frac{1}{T}\sum _{i=t+1}^T{r}_i$$

• $\gamma$折扣回报函数

$$R_t=\sum _{i=t+1}^{\infty }{\gamma }^{i-t}{r}_i$$

其中$R_t$是从$t$时刻状态$s_t$开始计算的回报，当执行某动作转移到下一个状态时产生第一个奖赏，因此从$t+1$时刻开始求和。$r_i$是第$i$步的单步奖赏，是一个随机变量。迭代因子$T⩾1$与折扣因子$\gamma <1$都对奖赏期望序列进行加权，在数学上使级数收敛。在物理意义上，$T$、$\gamma$越大表示考虑决策的长期回报；$T$、$\gamma$越小表示考虑决策的短期收益。特别地，当$T=1$或$\gamma =0$表示单步强化学习任务。

3 策略评估函数

策略评估函数分为两种

• 状态值函数$V^{\pi }\left(s\right)$
  表示从$t$时刻状态$s$出发，采用策略$\pi$带来的回报期望
  $$\{\begin{array}{l}{V}_T^{\pi }\left(s\right)=\mathbb{E}\left[R_t\right]{\mid }_{s_t=s}^{}=\frac{1}{T}{\sum }_{i=t+1}^T\mathbb{E}\left[r_i\right]{\mid }_{s_t=s}^{}\\ V_{\gamma }^{\pi }\left(s\right)=\mathbb{E}\left[R_t\right]{\mid }_{s_t=s}^{}={\sum }_{i=t+1}^{\infty }{\gamma }^{i-t}\mathbb{E}\left[r_i\right]{\mid }_{s_t=s}^{}\end{array}$$
• 状态动作值函数$Q^{\pi }\left(s,a\right)$
  表示从$t$时刻状态$s$出发，执行动作$a$后再采用策略$\pi$带来的回报期望
  $$\{\begin{array}{l}{Q}_T^{\pi }\left(s,a\right)=\mathbb{E}\left[R_t\right]{\mid }_{s_t=s,a_t=a}^{}=\frac{1}{T}{\sum }_{i=t+1}^T\mathbb{E}\left[r_i\right]{\mid }_{s_t=s,a_t=a}^{}\\ Q_{\gamma }^{\pi }\left(s,a\right)=\mathbb{E}\left[R_t\right]{\mid }_{s_t=s,a_t=a}^{}={\sum }_{i=t+1}^{\infty }{\gamma }^{i-t}\mathbb{E}\left[r_i\right]{\mid }_{s_t=s,a_t=a}^{}\end{array}$$

其中$s_t$表示评估的初始状态，$a_t$表示在初始状态上采取的第一个动作

下面研究$V^{\pi }\left(s\right)$与$Q^{\pi }\left(s,a\right)$的关系。根据全概率公式，状态值函数$V^{\pi }\left(s\right)$可用状态动作值函数$Q^{\pi }\left(s,a\right)$加权得到

$$V^{\pi }\left(s\right)=\sum _{a\in A}P\left(a|s\right)Q^{\pi }\left(s,a\right)=\sum _{a\in A}\pi \left(s,a\right)Q^{\pi }\left(s,a\right)$$

以$T$步回报函数为例说明$Q^{\pi }\left(s,a\right)$如何用$V^{\pi }\left(s\right)$表示

$$\begin{array}{rl}{Q}_T^{\pi }\left(s,a\right)& =\frac{1}{T}\sum _{i=t+1}^T\mathbb{E}\left[r_i\right]{\mid }_{s_t=s,a_t=a}^{}\\ & =\frac{1}{T}\left[\mathbb{E}\left[r_{t+1}\right]{\mid }_{s_t=s,a_t=a}^{}+\sum _{i=t+2}^T\mathbb{E}\left[r_i\right]{\mid }_{s_t=s,a_t=a}^{}\right]\\ & =\frac{1}{T}\left[\sum _{s^{\prime }\in S}{P}_{s\to s^{\prime }}^a{R}_{s\to s^{\prime }}^a+\sum _{s^{\prime }\in S}{P}_{s\to s^{\prime }}^a\sum _{i=t+2}^T\mathbb{E}\left[r_i\right]{\mid }_{s_{t+1}=s^{\prime }}^{}\right]\\ & =\sum _{s^{\prime }\in S}{P}_{s\to s^{\prime }}^a\left[\frac{1}{T}{R}_{s\to s^{\prime }}^a+\frac{T-1}{T}\frac{1}{T-1}\sum _{i=t+1}^{T-1}\mathbb{E}\left[r_i\right]{\mid }_{s_t=s^{\prime }}^{}\right]\end{array}$$

即

$$Q_T^{\pi }\left(s,a\right)=\sum _{s^{\prime }\in S}{P}_{s\to s^{\prime }}^a\left[\frac{1}{T}{R}_{s\to s^{\prime }}^a+\frac{T-1}{T}{V}_{T-1}^{\pi }\left(s^{\prime }\right)\right]$$

同理有

$$Q_{\gamma }^{\pi }\left(s,a\right)=\sum _{s^{\prime }\in S}{P}_{s\to s^{\prime }}^a\left[R_{s\to s^{\prime }}^a+\gamma V_{\gamma }^{\pi }\left(s^{\prime }\right)\right]$$

4 贝尔曼期望方程

策略评估是给定一个策略$\pi$计算策略评估函数$V^{\pi }\left(s\right)$或$Q^{\pi }\left(s,a\right)$的过程，用于衡量策略的好坏。策略评估通常采用迭代法而非第三节中的定义计算

根据强化学习任务的马尔科夫性，多步强化学习中的某一步仅与上一步的状态和动作有关，将第三节的式子

• $V^{\pi }\left(s\right)={\sum }_{a\in A}P\left(a|s\right)Q^{\pi }\left(s,a\right)={\sum }_{a\in A}\pi \left(s,a\right)Q^{\pi }\left(s,a\right)$

• $Q_{\gamma }^{\pi }\left(s,a\right)={\sum }_{s^{\prime }\in S}{P}_{s\to s^{\prime }}^a\left[R_{s\to s^{\prime }}^a+\gamma V_{\gamma }^{\pi }\left(s^{\prime }\right)\right]$

互相代入，即可推导出强化学习的贝尔曼递推公式(Bellman Equation)或称贝尔曼期望方程，如下

$$\{\begin{array}{l}{V}_{\gamma }^{\pi }\left(s\right)={\sum }_{a\in A}\pi \left(s,a\right){\sum }_{s^{\prime }\in S}{P}_{s\to s^{\prime }}^a\left[R_{s\to s^{\prime }}^a+\gamma V_{\gamma }^{\pi }\left(s^{\prime }\right)\right]\\ Q_{\gamma }^{\pi }\left(s,a\right)={\sum }_{s^{\prime }\in S}{P}_{s\to s^{\prime }}^a\left[R_{s\to s^{\prime }}^a+\gamma {\sum }_{a^{\prime }\in A}\pi \left(s^{\prime },a^{\prime }\right)Q_{\gamma }^{\pi }\left(s^{\prime },a^{\prime }\right)\right]\end{array}$$

5 收敛性证明

上述迭代公式属于不动点方程。设贝尔曼期望算子为${\mathcal{B}}^{\pi }$，则

∣ ( B π V 1 π ) ( s ) − ( B π V 2 π ) ( s ) ∣ = ∣ γ ∑ a ∈ A π ( s , a ) ∑ s ′ ∈ S P s → s ′ a [ V 1 π ( s ′ ) − V 2 π ( s ′ ) ] ∣ ⩽ γ ∑ a ∈ A π ( s , a ) ∑ s ′ ∈ S P s → s ′ a ∣ V 1 π ( s ′ ) − V 2 π ( s ′ ) ∣    绝对值不等式 ⩽ γ ∑ a ∈ A π ( s , a ) ∑ s ′ ∈ S P s → s ′ a [ max ⁡ s ′ ′ ∣ V 1 π ( s ′ ′ ) − V 2 π ( s ′ ′ ) ∣ ] = γ ∥ V 1 π ( s ) − V 2 π ( s ) ∥ ∞ \begin{aligned}\left| \left( \mathcal{B} ^{\pi}V_{1}^{\pi} \right) \left( s \right) -\left( \mathcal{B} ^{\pi}V_{2}^{\pi} \right) \left( s \right) \right|&=\left| \gamma \sum_{a\in A}{\pi \left( s,a \right)}\sum_{s'\in S}{P_{s\rightarrow s'}^{a}}\left[ V_{1}^{\pi}\left( s' \right) -V_{2}^{\pi}\left( s' \right) \right] \right|\\&\leqslant \gamma \sum_{a\in A}{\pi \left( s,a \right)}\sum_{s'\in S}{P_{s\rightarrow s'}^{a}}\left| V_{1}^{\pi}\left( s' \right) -V_{2}^{\pi}\left( s' \right) \right|\,\, {\text{绝对值不等式}}\\&\leqslant \gamma \sum_{a\in A}{\pi \left( s,a \right)}\sum_{s'\in S}{P_{s\rightarrow s'}^{a}}\left[ \underset{s''}{\max}\left| V_{1}^{\pi}\left( s'' \right) -V_{2}^{\pi}\left( s'' \right) \right| \right] \\&=\gamma \left\| V_{1}^{\pi}\left( s \right) -V_{2}^{\pi}\left( s \right) \right\| _{\infty}\end{aligned} ∣(BπV1π​)(s)−(BπV2π​)(s)∣​= ​γa∈A∑​π(s,a)s′∈S∑​Ps→s′a​[V1π​(s′)−V2π​(s′)] ​⩽γa∈A∑​π(s,a)s′∈S∑​Ps→s′a​∣V1π​(s′)−V2π​(s′)∣绝对值不等式⩽γa∈A∑​π(s,a)s′∈S∑​Ps→s′a​[s′′max​∣V1π​(s′′)−V2π​(s′′)∣]=γ∥V1π​(s)−V2π​(s)∥∞​​

上述不等式对$\forall s\in S$都成立，不妨取

$$s=\arg \underset{s}{\max }\left|\left({\mathcal{B}}^{\pi }{V}_1^{\pi }\right)\left(s\right)-\left({\mathcal{B}}^{\pi }{V}_2^{\pi }\right)\left(s\right)\right|$$

则

$${\left|\left({\mathcal{B}}^{\pi }{V}_1^{\pi }\right)\left(s\right)-\left({\mathcal{B}}^{\pi }{V}_2^{\pi }\right)\left(s\right)\right|}_{\infty }⩽\gamma {\Vert V_1^{\pi }\left(s\right)-V_2^{\pi }\left(s\right)\Vert }_{\infty }$$

所以${\mathcal{B}}^{\pi }$是一个压缩映射，根据巴拿赫不动点定理，映射${\mathcal{B}}^{\pi }$存在唯一的不动点 。换言之，若需要求解状态值函数$V^{\pi }\left(s\right)$，可以任取一个值$V_0^{\pi }\left(s\right)$进行迭代，最终收敛到正确的$V^{\pi }\left(s\right)$值

$$\underset{k\to \infty }{\lim }{\left({\mathcal{B}}^{\pi }\right)}^k{V}_0^{\pi }=V^{\pi }$$

这就是强化学习中策略评估的理论保证

---

更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系