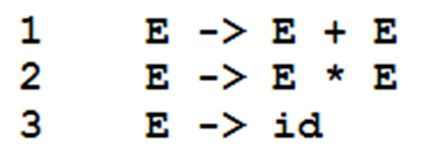如何使用Python开发自己的编译器
1. 前言
总所周知,编译器是一个将一种语言(源语言)翻译成另一种语言(目标语言)的程序,如果我们只想使用它,我们只需要将它看作一个黑盒子即可不必关心它的实现,如图1所示。

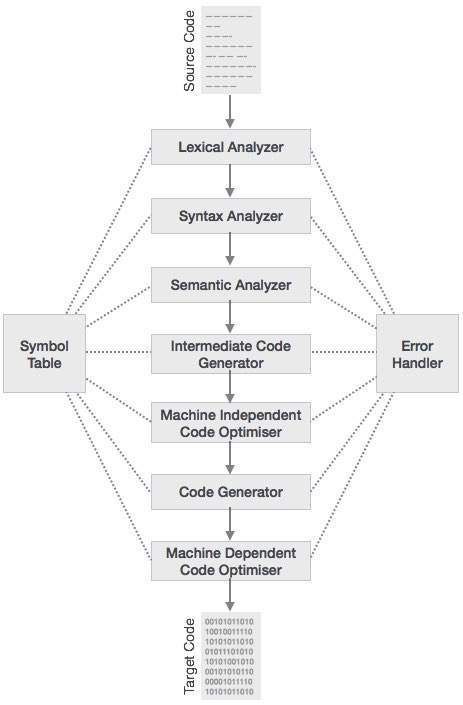
但是如果你想发明一种新的语言,你就需要了解它的内部构造了,因为要发明一门新语言,其实你需要做的就是编写一个新的编译器。实际上,编译器将源程序翻译成目标程序的过程可以分为词法分析、语法分析、语义分析以及目标代码生成等多个阶段,如图2所示。通常,我们称词法分析、语法分析、语义分析以及中间代码生成这几个阶段为前端,而代码优化以及目标代码生成为后端。根据使用场景的不同,其中有些阶段不是必须的,例如一个编译器可以没有中间代码以及代码优化。但是即便一个只包含词法分析、语法分析语义分析的简单编译器,如果需要从零开始也是比较困难的,需要非常熟悉编译原理。
由于编译原理太过复杂,为了能让开发一款编译器变得更高效,出现了很多编译器框架,例如著名的LLVM。在之前的文章LLVM,一堆积木的故事中介绍过,LLVM提供了所有编译器所需的组件,我们只需要增加或者替换一些特定组件,就能实现一个新的编译器。例如,只需要提供一个新的前端,你就能实现一个运行在目前LLVM所支持的硬件的上的全新语言。
那么要怎么快速的实现自己的前端呢?这就是我们今天的主角——PLY——所做的事情。
2. 铺垫
2.1. 词法分析器
词法分析的作用是将组成源程序的字符流识别成一个一个的记号(Token),并去除多余的空格以及注释等,方便语法分析器进行后续的语法分析,其工作原理如图3所示。

例如在C语言中,词法分析器会将int value = 100;这个表达式转变为下列的一个个记号:
int (keyword), value (identifier), = (operator), 100 (constant) and ; (symbol)
2.2. 语法分析器
语法分析器——也叫解析器——的作用就是将从词法分析器获得的记号流与给定的一条条规则进行比对,从而检测源程序中是否存在错误,这些规则称为产生式(Production)。如果源程序没有错误,词法分析器会输出一个解析树,也成为抽象语法树(AST)。语法分析的工作原理如图4所示。

2.3. BNF
既然词法分析器是通过产生式来判断源代码是否有错误,那么我们就得先知道产生式是什么东西。我们知道,每一种程序设计语言都有其描述语法规则的结构,而这些描述语法的结构就可以用上下文无关文法——也就是BNF范式——来描述。
BNF是由John Backus以及Peter Baur提出的,它可以用于描述上下文无关语言,例如可以用于描述以一个语言中的加减乘除操作,其形态如图5所示。组成BNF范式的每一条规则就是一个产生式。
如上图BNF范式所示,其描述了某种语言中的加法和乘法操作,例如在算数表达式24 * 43中,经过词法分析会得到24、*、43这三个记号,其中24、43都是id。我们首先通过第三条产生式将24、43都替换成了E,得到了E * E,之后,我们发现产生式2正好可以匹配,说明算数表达式24 * 43是没有语法错误的。反之,由于这个BNF范式中没有定义减法的产生式,因此对于算数表达式88 - 43,最终找不到与它想匹配的产生式,因此就会出现语法错误。
2.4.Lex & Yacc
Lex 与 Yacc是用于构建编译器前端的两个工具,他们分别由Eric Schmidt 与Stephen Johnson于上世纪70年代创造。Lex用于词法分析,而Yacc(Yet Another Compiler Compiler)用于语法分析,后续的许多解析器都是他们的变种。
而今天介绍的PLY,就是Lex以及Yacc的纯Python实现
2.5. PLY简介
PLY,全称为Python Lex-Yacc,是Lex以及Yacc的纯Python实现,用于构建编译器的前端,Lex负责词法分析,Yacc负责语法分析。他们拥有与传统的Lex\Yacc一样的功能。PLY这个库的结构很简单,就包含两个重要文件lex.py 以及yacc.py。使用的时候只需要在你的工程下新建一个目录并命名为ply然后将这两个文件拷贝进去,然后通过import ply.lex以及import ply.yacc这两个语句导入就可以使用了。
3. PLY举例
我们使用PLY的时候需要遵守一定的规则,根据需要定义一些我们需要的变量以及函数。PLY运行的时候会通过自省的方式获取到我们定义的变量以及参数用于进行词法分析以及语法分析。
3.1. Lex
首先我们来看看如果我们要使用Lex我们需要做些什么,我们将以下面的代码为例子作为讲解。
import ply.lex as lex
# List of token names. This is always required
tokens = (
'NUMBER',
'PLUS',
'MINUS',
'TIMES',
'DIVIDE',
'LPAREN',
'RPAREN',
)
# Regular expression rules for simple tokens
t_PLUS = r'\+'
t_MINUS = r'-'
t_TIMES = r'\*'
t_DIVIDE = r'/'
t_LPAREN = r'\('
t_RPAREN = r'\)'
# A regular expression rule with some action code
def t_NUMBER(t):
r'\d+'
t.value = int(t.value)
return t
# Define a rule so we can track line numbers
def t_newline(t):
r'\n+'
t.lexer.lineno += len(t.value)
# A string containing ignored characters (spaces and tabs)
t_ignore = ' \t'
# Error handling rule
def t_error(t):
print("Illegal character '%s'" % t.value[0])
t.lexer.skip(1)
# Build the lexer
lexer = lex.lex()
在上面的例子中,首先我们需要定义一个名叫tokens的列表,这个列表中包含了所有可能被Lex所处理的记号的名字,想要使用lex.py这个列表是必须要有的,因为Lex的以及就是将输入的源代码转换成一个一个记号,因此你需要定义一个记号的列表告诉Lex你的源代码都可能出现些什么记号,yacc.py也会用到这个列表。
之后,我们需要为每一个记号的名字定义一个正则表达式,这些正则表达式的规则必须是与Python正则表达式库re相兼容的,因为lex.py使用正则表达式来识别记号,并且每个正则表达式的名字都是以t_开头,后面紧跟着其对应的记号的名字。例如我们给加号+定义的这则表达式为t_PLUS = r'\+'。如果我们还希望识别到某些特定的记号的时候进行一些自定义的操作,我们可以使用函数代替,例如上面例子中当识别到数字的时候我们希望将其转换为对应的数值类型,我们便将t_NUMBER = r'\d+变成了下面的样子:
def t_NUMBER(t):
r'\d+'
t.value = int(t.value)
return t
其中函数的参数t是类LexToken的实例,LexToken有四个常用属性,分别是(type, value, lineno, lexpos)。函数的名字与普通的记号的遵循一样的规则,都是以t_开头。函数的第一行是识别该记号的正则表达式,接下来是对识别到的记号的操作,最后需要将这个LexToken实例返回,如果该函数没有返回值,则这个被处理的记号就会被直接丢弃。
紧接着,我们定义了一个特殊的函数t_nemline()用于记录行数以及一个t_error()用于处理错误。
最后我们执行lexer = lex.lex()去生成一个词法分析器。
3.2. Yacc
yacc.py是PLY中Yacc的实现,与lex.py类似, 我们也通过一个例子来说明在使用yacc.py之前我们需要做的事情。使用yacc.py之前,你应该已经有了一个BNF范式来描述你的语言。
例如对于算数运算操作,我们定义了如图4所示BNF范式。

有了这个BNF范式之后,想要使用PLY的yacc模块来进行语法分析,所需要做的就是为每个产生式编写一个处理函数。下面的例子就是根据图4的BNF范式写出的对应的产生式的处理函数,每个函数可以只对应一个语法规则,也可以对应同一类型的多个语法规则。例如可以把下面例子中分开的加减乘除四个产生式的处理函数写成一个:
def p_expression_binop(p):
'''expression : expression '+' expression
| expression '-' expression
| expression '*' expression
| expression '/' expression
'''
if p[2] == '+' :
p[0] = p[1] + p[3]
elif p[2] == '-':
p[0] = p[1] - p[3]
elif p[2] == '*':
p[0] = p[1] * p[3]
elif p[2] == '/':
p[0] = p[1] / p[3]
import ply.yacc as yacc
# Get the token map from the lexer. This is required.
from calclex import tokens
def p_expression_plus(p):
'expression : expression PLUS term'
p[0] = p[1] + p[3]
def p_expression_minus(p):
'expression : expression MINUS term'
p[0] = p[1] - p[3]
def p_expression_term(p):
'expression : term'
p[0] = p[1]
def p_term_times(p):
'term : term TIMES factor'
p[0] = p[1] * p[3]
def p_term_div(p):
'term : term DIVIDE factor'
p[0] = p[1] / p[3]
def p_term_factor(p):
'term : factor'
p[0] = p[1]
def p_factor_num(p):
'factor : NUMBER'
p[0] = p[1]
def p_factor_expr(p):
'factor : LPAREN expression RPAREN'
p[0] = p[2]
# Error rule for syntax errors
def p_error(p):
print("Syntax error in input!")
# Build the parser
parser = yacc.yacc()
while True:
try:
s = raw_input('calc > ')
except EOFError:
break
if not s: continue
result = parser.parse(s)
print(result)
与给Lex模块定义记号列表类,这些为产生式编写的函数也要准守一定的规则:
- 函数有两部分组成:1)docstring,对应的是该函数所处理的产生式;2)函数体,代表的是这个产生式的语义;
- 每个函数有且只有一个参数
p(当然参数的名字是任意的,如果乐意你可以叫它做狗蛋),这个p是一个数组,每个元素代表的是对应的语法中的符号的值,例如图5所示的函数处理的是expression : expression PLUS term这条语法规则,那么从p[0]到p[3]所对应的值分别如图中所示;

- 函数必须以
p_开头,后面的名字也不重要,例如你可以吧p_expression_plus改成p_dogegg; - 函数出现的顺序是有意义的,必须按照BNF范式定义的顺序来定义处理产生式的函数,还拿图4的BNF范式举例,定义处理
assign : NAME EQUALS expr的产生式的函数必须在处理其他产生的函数之前。
4. 例子
下面,我们就将上面的片段整合一下,开发一个新的语言的编译器,我们就叫它Hello World编译器。它可以编译任何加减乘除的数学表达式,然后执行这个表达式,执行的结果就是数学表达式计算得到结果是多少,就输出多少个Hello World字符串,我们这门语言可能是最容易打出Hello World的语言了。
from utils import *
sys.path.insert(0, "../..")
tokens = (
'NAME', 'NUMBER'
)
literals = ['=', '+', '-', '*', '/', '(', ')', ',']
# Tokens
t_NAME = r'[a-zA-Z_][a-zA-Z0-9_.:]*'
def t_NUMBER(t):
r'\#?\d+'
if t.value.startswith('#'):
t.value = int(t.value[1:])
else:
t.value = int(t.value)
return t
# Get the comments and discard it, therefore there is not return statement
# Note: only inline comment are permit
t_ignore = " \t"
def t_newline(t):
r'\n+'
t.lexer.lineno += t.value.count("\n")
def t_error(t):
print("Illegal character '%s'" % t.value[0])
t.lexer.skip(1)
# Build the lexer
import ply.lex as lex
lexer = lex.lex()
# Parsing rules
precedence = (
('left', '+', '-'),
('left', '*', '/'),
('right', 'UMINUS'),
)
# dictionary of names
names = {}
alias = {}
def p_statement_assign(p):
'''statement : NAME "=" expression
'''
if p[2] == '=':
names[p[1]] = p[3]
def p_statement_expr(pppp):
'''statement : expression'''
for i in range(pppp[1] ):
print('Hello world!')
def p_expression_binop(p):
'''expression : expression '+' expression
| expression '-' expression
| expression '*' expression
| expression '/' expression
'''
if p[2] == '+' :
p[0] = p[1] + p[3]
elif p[2] == '-':
p[0] = p[1] - p[3]
elif p[2] == '*':
p[0] = p[1] * p[3]
elif p[2] == '/':
p[0] = p[1] / p[3]
def p_expression_uminus(p):
"expression : '-' expression %prec UMINUS"
p[0] = -p[2]
def p_expression_group(p):
'''expression : '(' expression ')'
| '{' expression '}' '''
p[0] = p[2]
def p_expression_list(p):
'''
expression : expression
| expression ',' expression
'''
def p_expression_number(p):
"expression : NUMBER"
p[0] = p[1]
def p_expression_name(p):
"expression : NAME"
try:
if p[1] in alias:
p[0] = names[alias[p[1]]]
else:
p[0] = names[p[1]]
except LookupError:
print("Undefined name '%s'" % p[1])
p[0] = 0
def p_error(p):
if p:
print("Syntax error at '%s'" % p.value)
else:
print("Syntax error at EOF")
import ply.yacc as yacc
parser = yacc.yacc()
while True:
try:
s = input('hello world calc > ')
except EOFError:
break
if not s:
continue
yacc.parse(s)
![]()
首发于个人微信公众号TensorBoy。微信扫描上方二维码或者微信搜索TensorBoy并关注,及时获取更多最新文章!
C++ | Python | Linux | 原理 | 源码,有一起玩耍的么?
5. References
[1] http://www.dabeaz.com/ply/ply.html#ply_nn24
[2] Compilers: Principles, Techniques and Tools: Chapter#2