【代码随想录 | Leetcode | 第四天】数组 | 螺旋矩阵 | 59-54
前言
欢迎来到小K的Leetcode|代码随想录|专题化专栏,今天将为大家带来螺旋矩阵的分享✨
目录
- 前言
- 59. 螺旋矩阵 II
- 54. 螺旋矩阵
- 总结
59. 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
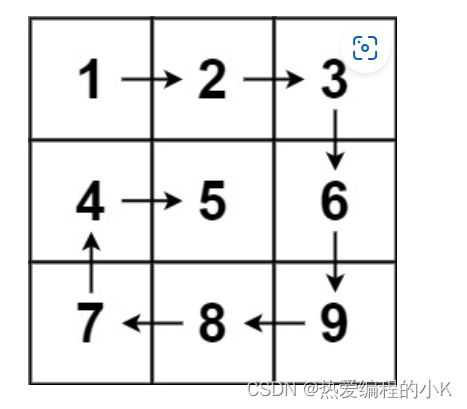
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
提示:
1 <= n <= 20
思路:
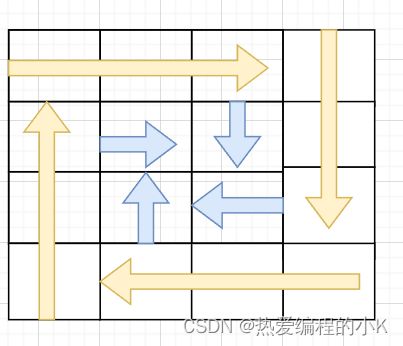
本类型题目其实都不涉及什么算法,就是模拟螺旋顺序打印的过程,下面我们来模拟一下
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
但是我们可以看出,这样一圈一圈的模拟下去,边界条件非常多,很容易出错,这时候我们第一节学的二分法中用的循环不变量规则就非常重要了
class Solution {
public:
vector<vector<int>> generateMatrix(int n)
{
vector<vector<int>> res(n,vector<int>(n,0));
int startx=0,starty=0; //定义每循环一个圈的起始位置
int loop=n/2; //每个圈循环几次,如果n为奇数3,那么loop=1,只循环一圈
int mid=n/2; //矩阵中间位置,例如n为3,中间的位置为【1,1】
int count=1; //用来给矩阵元素赋值的
int offset=1; //用来控制循环遍历长度
int i,j;
while(loop--)
{
i=startx,j=starty;
//左闭右开
for(j=starty;j<starty+n-offset;j++) res[startx][j]=count++;
for(i=startx;i<startx+n-offset;i++) res[i][j]=count++;
for(;j>starty;j--) res[i][j]=count++;
for(;i>startx;i--) res[i][j]=count++;
//第二圈开始,起始位置要各自加一
startx++,starty++;
offset+=2;
}
//如果n为奇数,则需要单独给矩阵之间的位置赋值
if(n%2) res[mid][mid]=count;
return res;
}
};
上面代码中已经把模拟过程详细讲解了一遍,这里再对以下两点特别说明一下:
starty+n-offset:为什么这里要加上起始位置,因为第二圈开始起始坐标不为0offset+=2:为什么要加2,因为每走一圈就少了两端的元素,赋初值为1是因为遵循左闭右开的原则- 上边有3 * 3和4 * 4的模拟图
54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
m ==matrix[i].length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100
做这道题目我们也是在遵循循环不变量规则,看下面的代码中我们用的前置++,而不是后置++,细品(左开右闭),这里判断循环结束的方法也非常巧妙,判断4个边界是否有冲突,有冲突就退出循环
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix)
{
vector<int> ans;
if(!matrix.size()) return ans;
int up=0,down=matrix.size()-1,left=0,right=matrix[0].size()-1;
while(true)
{
for(int i=left;i<=right;++i) ans.push_back(matrix[up][i]);
if(++up>down) break;
for(int j=up;j<=down;++j) ans.push_back(matrix[j][right]);
if(--right<left) break;
for(int k=right;k>=left;--k) ans.push_back(matrix[down][k]);
if(--down<up) break;
for(int L=down;L>=up;--L) ans.push_back(matrix[L][left]);
if(++left>right) break;
}
return ans;
}
};
总结
✨做这种类型的题目就是要多画图模拟,思路清晰就好办了,还有就是注意边界条件(遵循循环不变量规则)