【C刷题笔记】找单身狗问题

目录

版本1:在数组内只有一个元素没有成对出现

版本2:在数组内有两个元素没有成对出现

第一步:异或所有元素,异或就是相同为0，相异为1

第二步:计算ret的二进制中哪一位元素是1

第三步:开始分组异或

1.分组:

2.异或

---

版本1:在数组内只有一个元素没有成对出现

单身狗
只有一个数字出现一次，其他数数字都是成对出现的，找出只出现一次的数字
1 2 3 4 5 1 2 3 4 

分析:
所有的数字异或在一起，异或的规则:
1.a^a=0 -->任何数异或本身等于0

2.a^0=a -->任何数异或0等于任何数

也就是说此数组的所有元素（除了5）异或之后就为0，再和5异或，最终结果就是5

找单身狗问题:

#include
int single_num(int* nums, int sz)
{
	int x = 0;
	for (int i = 0; i < sz; i++)
	{
		x ^= nums[i];
	}
	return x;
}
int main()
{
	int nums[] = { 1,2,3,4, 5, 1, 2, 3 ,4 };
	int sz = sizeof(nums) / sizeof(nums[0]);
	int ret = single_num(nums, sz);
	printf("单身狗数字为:%d", ret);
}

执行: 

版本2:在数组内有两个元素没有成对出现

一个数组中只有两个数字是出现一次，其他所有数字都出现了两次。
编写一个函数找出这两个只出现一次的数字。
例如：
有数组的元素是：1，2，3，4，5，1，2，3，4，6

分析:

此版本的单身狗是在一个数组内一次找两个单身狗(没有成对出现的)，就比如上面的,5,6都是没有第二个相同的数

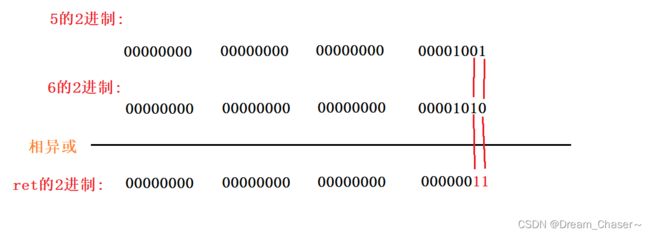
由版本一,分析可知相同元素相异或就为0,0和5，6异或之后肯定不为0,下面图解:

第一步:异或所有元素,异或就是相同为0，相异为1

 第二步:计算ret的二进制中哪一位元素是1

 

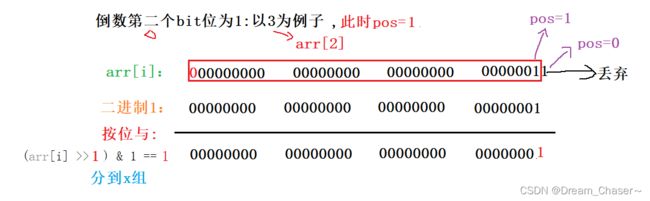
以此类推,用一个for循环遍历32bit位:(ret>>i)与i相按位与,找到所有1所在的位置,也就是用pos表示。

第三步:开始分组异或

1.分组:

这是倒数第一位bit位为1的情况:

 这是倒数第一位bit位为0的情况:

 

 这是倒数第二位bit位为1的情况:

  这是倒数第二位bit位为0的情况:

2.异或

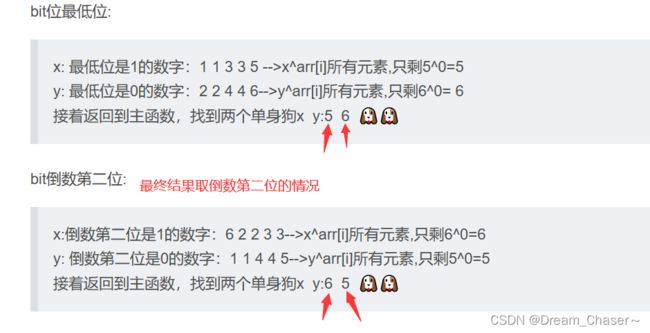
bit位最低位:

x: 最低位是1的数字：1 1 3 3 5 -->x^arr[i]所有元素,只剩5^0=5
y: 最低位是0的数字：2 2 4 4 6-->y^arr[i]所有元素,只剩6^0= 6

接着返回到主函数，找到两个单身狗x  y:5  6 

bit倒数第二位:

x:倒数第二位是1的数字：6 2 2 3 3-->x^arr[i]所有元素,只剩6^0=6
y: 倒数第二位是0的数字：1 1 4 4 5-->y^arr[i]所有元素,只剩5^0=5

接着返回到主函数，找到两个单身狗x  y:6  5 

实例代码:

#include
void find_single_dog(int* arr, int sz, int* x, int* y)
{
	int i = 0;
	int ret = 0;
	//1.异或所有元素
	for (i = 0; i < sz; i++)
	{
		ret ^= arr[i];
	}
	//2.计算ret的二进制中哪一位元素是1
	int pos = 0;
	for (i = 0; i < 32; i++)//32bit位
	{
		if ((ret >> i) & 1 == 1)
		{
			pos = i;
		}
	}
	//3.开始分组异或
	for (i = 0; i < sz; i++)
	{
		if ((arr[i] >> pos) & 1 == 1)
		{
			*x ^= arr[i];
		}
		else
		{
			*y ^= arr[i];
		}
	}
}
int main()
{
	int arr[] = { 1,2,3,4,5,1,2,3,4,6};

	int sz = sizeof(arr) / sizeof(arr[0]);
	int x = 0;
	int y = 0;
	find_single_dog(arr, sz, &x, &y);
	printf("单身狗是:%d %d\n", x, y);
	return 0;
}

执行:因为中途(arr[i]>>pos)&1使得x和y的两个单身狗移动过位置,取最后一次的情况。