Python综合评价模型(六)层次分析法
文章目录
-
-
- 第一步 导入第三方库和案例数据
- 第二步 标准化数据
- 第三步 判断矩阵一致性检验
- 第四步 计算权重
- 第五步 计算综合得分
- 第六步 导出综合评价结果
- 下期预告: P y t h o n 综合评价模型(七)变异系数法 \textcolor{RoyalBlue}{下期预告 : Python综合评价模型(七)变异系数法} 下期预告:Python综合评价模型(七)变异系数法
- 关注公众号“ T r i H u b 数研社”发送“ 230319 ”获取案例数据和代码 \textcolor{RoyalBlue}{关注公众号“TriHub数研社”发送“230319”获取案例数据和代码} 关注公众号“TriHub数研社”发送“230319”获取案例数据和代码
-
层次分析法是建立递阶层次结构,通过比较评价准则(评价指标)的两两重要程度对评价方案(评价对象)进行综合评价的方法
递阶层次结构从上到下一般包括“目标层”、“准则层”、“方案层”
举个例子:我们计划在周末观看一部超英电影
“目标层”——选择一部超英电影
“准则层”——票价、剧情、特效、演员
“方案层”——漫威的《蚁人3》和DC的《沙赞2》
第一步 导入第三方库和案例数据
import numpy as np
import pandas as pd
#按指定路径导入数据,以“地区”为索引(文件路径需按实际情况更换)
data = pd.read_excel(r'C:/Users/AROUS/Desktop/综合评价数据.xlsx', index_col = '地区')
data
#按指定路径导入判断矩阵(文件路径需按实际情况更换)
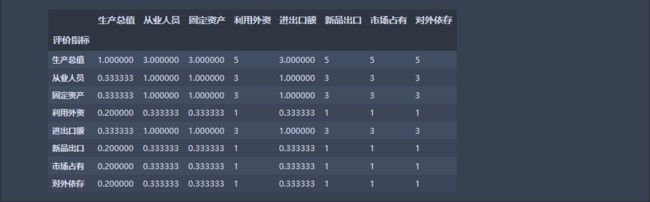
matrix = pd.read_excel(r'C:/Users/AROUS/Desktop/综合评价数据.xlsx', index_col = '判断矩阵', sheet_name = '层次分析')
matrix
判断矩阵是一个二维方阵,方阵的元素是评价指标按重要程度两两比较得到的分值
判断矩阵具有三方面特点:
- 特点1: a i j a_{ij} aij表示与指标j相比,指标i的重要程度分值
- 特点2:当i=j时表示指标自己和自己比,重要程度分值为1(同等重要),即判断矩阵的主对角线元素均为1
- 特点3: a i j a_{ij} aij>0 且 a i j a_{ij} aij× a j i a_{ji} aji=1,也就是判断矩阵为正互反矩阵
第二步 标准化数据
#定义z-score标准化函数
def z_score(x):
return (x - x.mean()) / x.std()
#使用z-score标准化函数标准化数据
data_z = data.apply(z_score, 0)
data_z
第三步 判断矩阵一致性检验
C R = C I R I CR=\frac{CI}{RI} CR=RICI
CR≥0.1判断矩阵未通过一致性检验
CR<0.1判断矩阵通过一致性检验
C I = λ m a x − n n − 1 CI=\frac{\lambda_{max}-n}{n-1} CI=n−1λmax−n
RI值是先从1-9及其倒数中随机抽取数字构造500个正互反矩阵,再计算500个正互反矩阵最大特征根的均值,最后根据公式 R I = λ m a x ˉ − n n − 1 RI=\frac{\bar{\lambda_{max}}-n}{n-1} RI=n−1λmaxˉ−n求得,一般情况下,可通过查表直接获取
| 矩阵维度n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RI值 | 0.00 | 0.00 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 | 1.51 | 1.54 | 1.56 | 1.58 | 1.59 |
#定义CR值计算函数
#函数linalg.eig用于计算矩阵的特征根和特征向量
def calc_cr(df):
n = len(df)
eig_val, eig_vec = np.linalg.eig(df.values)
eig_val_max = max(eig_val)
ci = (eig_val_max - n) / (n - 1)
ri = [0, 0, 0.58, 0.90, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49, 1.51, 1.54, 1.56, 1.58, 1.59]
cr = ci / ri[n]
return cr
#函数real用于获取一个复数的实数部分
cr = calc_cr(matrix)
print('CR值为:{:.4f}'.format(cr.real))
if cr >= 0.1:
print('判断矩阵未通过一致性检验')
else:
print('判断矩阵通过一致性检验')
第四步 计算权重
可选择使用算术平均法、加权平均法和特征向量法计算评价指标权重
暂以算术平均法举例说明,加权平均法和特征向量法将在后续推出的综合评价模型系列课程补充介绍
- 第一步 对判断矩阵的每列归一化
- 第二步 对第一步结果的每行求和
- 第三步 对第二步结果的每个元素除以n,n为判断矩阵维度
#定义算术平均法计算权重函数
def arith_mean_weight(df):
#对判断矩阵按列归一化
norm = df.apply(lambda x: x/x.sum(), axis = 0)
#按行求和,并除以n
weight = norm.sum(axis = 1)/len(df)
return weight
w1 = arith_mean_weight(matrix)
w1
第五步 计算综合得分
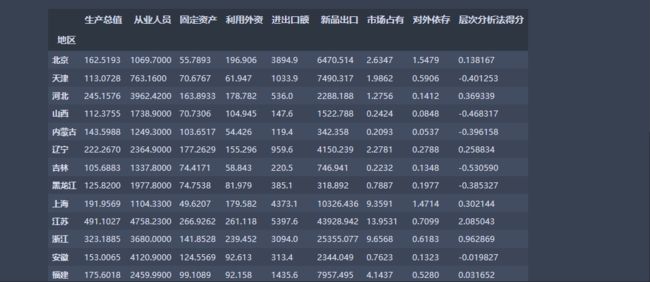
data['层次分析法得分'] = data_z.dot(w1)
data
第六步 导出综合评价结果
data.to_excel('层次分析法综合评价结果.xlsx', index = True)