【C语言】_3.函数
目录
1.函数的概念
2.C语言中函数的分类
3.函数的参数
4.函数的调用
正文:
1.函数的概念
函数就是一个子程序,用于完成某项特定任务,且相较于其他代码,具备相对的独立性。
2.C语言中函数的分类
(1)库函数:
① 定义:C语言中已经设计好的可以直接使用的函数,将C语言常用的功能实现成函数,集成为库,如printf scanf strlen;
② 示例:IO函数(输入输出函数),字符串操作函数,字符操作函数,内存操作函数,时间/日期函数,数学函数等等;
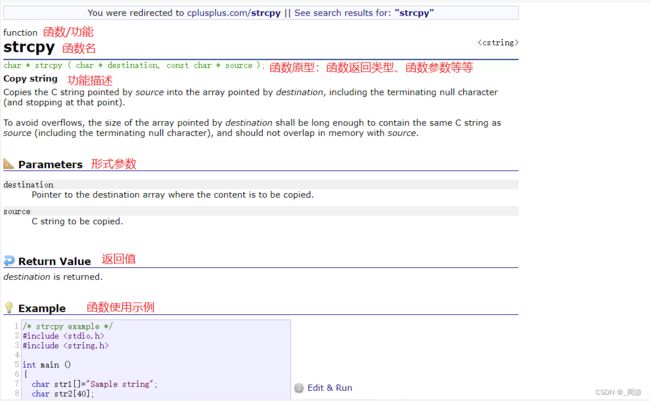
详细示例1:strcpy:
#include
#include
int main()
{
char arr1="abcdef";
char arr2=[20]={0};
//利用函数将arr1中的字符串拷贝到arr2中去
strcpy(arr2,arr1);
printf("%s\n",arr2);
return 0;
} 详细示例2:memset:
#include
#include
int main()
{
char arr[] = "hello world";
//将ello 改成xxxxx
memset(arr+1, 'x', 5);
printf("%s\n", arr);
return 0;
} 注意memset的特点是a.设置内存的时候都是以字节为单位的,b.每个字节的内容都是一样的;
(2)自定义函数:
自定义函数的函数名、返回值类型与函数参数都是程序员自行设计的。
示例:写一个函数求两个整数中的较大值
典型错误代码:
#incldue
void Swap1(int x,int y);
int main()
{
int a,b;
scanf("%d%d",&a,&b);
printf("a=%d b=%d\n",a,b);
Swap(a,b);
printf("a=%d b=%d\n",a,b);
return 0;
}
void Swap1(int x,int y)
{
int temp=0;
temp=x;
x=y;
y=temp;
} 注意当实参传给形参的时候,形参是实参的一份临时拷贝,对形参的修改不会影响实参。
正确代码:
#include
void Swap2(int* pa, int* pb);
int main()
{
int a, b;
scanf("%d%d", &a, &b);
printf("a=%d b=%d\n", a, b);
Swap(&a, &b);
printf("a=%d b=%d\n", a, b);
return 0;
}
void Swap2(int* pa, int* pb)
{
int temp = 0;
temp = *pa;
*pa = *pb;
*pb = temp;
} 通过对函数传递地址,再解引用对地址存放内容进行修改操作,就将a,b与x,y建立了联系,此时的修改才产生了意义。
3.函数的参数
3.1实际参数(实参)
真实传递给函数的参数叫实参。实参可以是常量、变量、表达式、函数等等。无论实参是什么类型的量,在进行函数调用时,它们都必须有确定的值,以便把这些值传递给形参。
在上例代码中,传递给Swap1中的a,b和传递给Swap2的&a,&b都是实际参数。
3.2 形式参数(形参)
形式参数是函数名后括号中的变量,形式参数只在函数被调用的过程中才分配内存单元进行实例化,故而称为形式参数。形式参数当函数调用完就销毁了,所以形式参数只在函数中有效。
在上例代码中,Swap1 中的x,y和Swap2 中的pa pb都是形式参数。
4.函数的调用
4.1 传值调用
函数的形参和实参分别占有不同内存块,对形参的修改操作不会影响实参。
上述代码中Swap1 是传值调用
4.2 传址调用
5.函数的嵌套调用和链式访问
#include
void new_line()
{
printf("hehe\n");
}
void three_line()
{
int i = 0;
for(i=0; i<3; i++)
{
new_line();
}
}
int main()
{
three_line();
return 0;
} 函数可以嵌套调用,但是不可以嵌套定义。
5.2链式访问
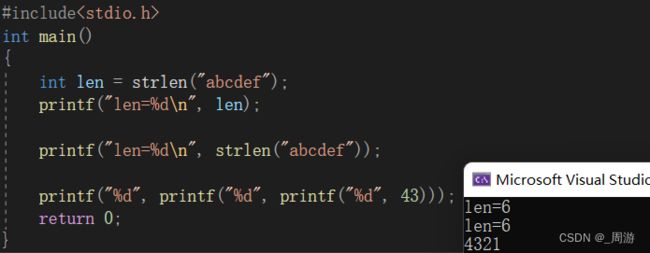
链式访问就是把一个函数的返回值作为1另外一个函数的参数
6.函数的声明和定义
6.1 函数的声明
仅仅表明函数的存在,说明函数的参数,函数名以及返回类型即可,不需要具体实现函数的功能。
#include
int Add(int x, int y); //函数的声明
int main()
{
int a, b;
scanf("%d%d", &a, &b);
int sum = Add(a, b);
printf("%d\n", sum);
return 0;
}
int Add(int x, int y) //函数的定义
{
return x + y;
} 函数的声明存在的意义是大型代码分块时,需要分文件写代码。一个函数可以称为一个模块,比如上例的实现可以分为Add.c(函数的定义)和Add.h(函数的声明),二者并称为加法模块。而后在test.c文件中只需要引头文件#include"Add.h",就可以正常使用了。同时分离头文件和源文件,编译成静态库就可以很好地隐藏源文件中的函数实现功能。(点击项目名称右击选择属性,在常规中选择配置类型为静态库并应用,然后在导航栏选择生成解决方案,就可以生成Add.lib的文件)然后仅使用函数声明者在头文件添加#pragma comment(lib,"add.lib")导入静态库即可。
7.函数的递归
7.1 递归的定义
函数调用自身的编程技巧称为递归。
主要思考方式在于大事化小。
7.2 递归的条件
(1)存在限制条件,当满足这个限制条件时,递归不再继续。
(2)每次递归调用之后越来越接近这个限制条件。
示例一:请写代码实现:接收一个无符号整型值,按顺序打印它的每一位。
#include
void print(int n)
{
if (n > 9)
{
print(n / 10);
}
printf("%d ", n % 10);
n = n % 10;
}
int main()
{
unsigned int num = 0;
scanf("%d", &num);
print(num); //print函数的功能是将num的每一位按顺序打出来
return 0;
} 示例二:请写代码实现:在不创建临时变量的条件下计算字符串长度
#include
int my_strlen(char* str)
{
if(*str != '\0')
{
return 1 + my_strlen(str + 1);
}
else
return 0;
}
int main()
{
char arr[] = "abcdef";
int len =my_strlen(arr);
printf("%d\n",len);
return 0;
} 7.3 递归与迭代
示例一:请编写代码实现:用递归方法实现n!
#include
int Fac(int n)
{
if (n <= 1)
return 1;
else
return n * Fac(n - 1);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fac(n);
printf("%d\n", ret);
return 0;
} 示例二:求第n个斐波那契数
法一:
#include
int Fib(int n)
{
if (n <= 2)
return 1;
if (n > 2)
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
} 按照递归思想可写出如上代码,然而当我们需要计算的斐波那契数字靠后时,比如需要计算第五十个斐波那契数字,发现需要编译的时间非常长。
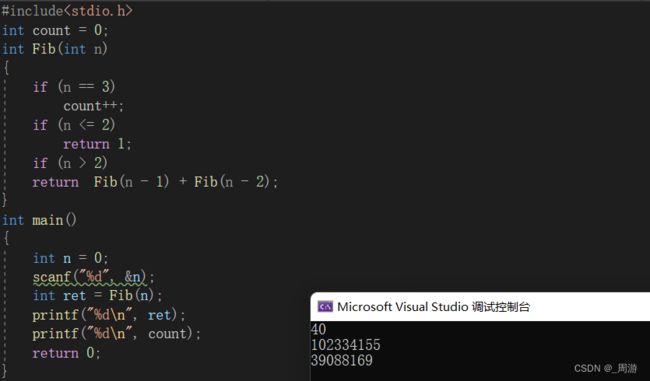
我们仔细观察该代码,发现该算法的弊端在于计算第n个数字则需要计算出第n-1和第n-2个,需要计算第n-1个数字又需要计算出第n-2和第n-3个数字......即从第三位开始,计算出每一个数字都需要计算它前之前的两个数字,这样的算法在调用中存在许多大量重复计算,比如我们可以大概计算一下第三个斐波那契数字在计算第40个斐波那契数字时被计算了多少次,代码及其运行结果如下:
可见仅仅是计算第40个斐波那契数字,第三个斐波那契数字就被重复计算了千万数量级次。这样的算法效率是非常低的,故而需要改进:
#include
int Fib(int n)
{
int a = 1;
int b = 1;
int c = 1;
while (n >= 3)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
} 放弃递归方法,用循环来完成斐波那契的计算可以避免大量重复计算,效率更高。
6.函数栈帧的创建和销毁
ps:寄存器:
包括eax,ebx,ecx,edx等,还有ebp,esp这两个寄存器中存放的是地址,这两个地址是用来维护函数栈帧的。
每一个函数调用都要在栈区创建一块空间。
以简单的求和函数为例:
求和函数代码:
int Add(int x, int y)
{
int z = 0;
z = x + y;
return z;
}
#include
int main()
{
int a = 10;
int b = 20;
int c = 0;
c = Add(a, b);
printf("%d\n", c);
return 0;
}
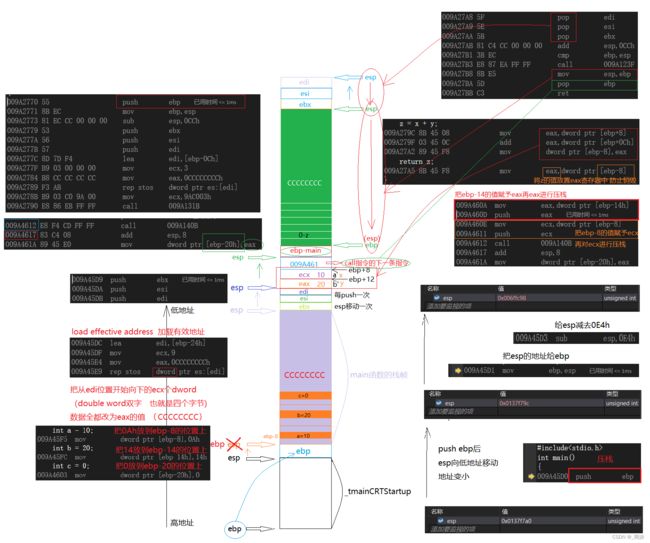
图示函数调用时栈帧的创建和销毁: