模拟退火算法
求某个目标函数的最值
爬山法
首先我们通过爬山法来引出模拟退火算法
我们先看一个例子:求函数的最值
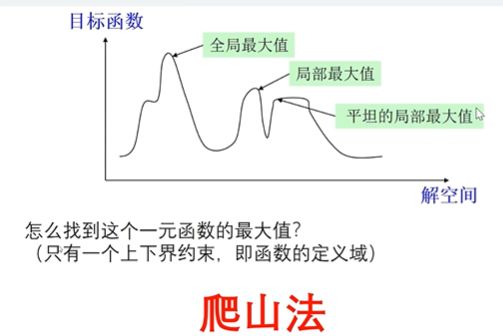
我们用爬山法解决这个问题的步骤
1、在解空间中随机生成一个初始解(图中小黄点就是我们生成的初始解)

2、根据初始解的位置,我们有两种决策,一种是向左邻域,一种是向右邻域走一步(走的步长越小越好,但是越小的话计算量会更大)
3、比较不同走法下目标函数的大小,决定下一步往哪个方向走,在上面的图上是向左走,目标函数的值更大,因此我们应该向左走一步
4、不断重复这个步骤,直到我们找到一个极大值点,此时我们结束搜索。
只要思考一下,我们可以明显的看出爬山法的缺点是特别容易找到局部最优解。爬山法的本质是贪心算法。这里我们的主角马上就要登场了,模拟退火算法能很好地解决上面的问题,模拟退火引入了一个概率帮助我们跳出局部最优解从而搜索到全局最优解。
模拟退火算法

模拟退火的核心思想是以一定的概率接收这个解
解决方法:
为了不直接拒绝xj,我们定义一个接收的概率p,p位于[0, 1]之间,且f(xj)和f(xi)越接近,p越大(这种想法很直观,新解和旧解的函数值越接近我们就越愿意接受新解)
p 正比于|1/(f(xj)- f(xi))|
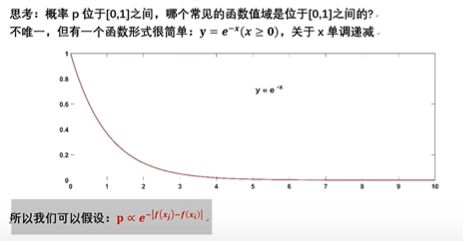
这里当p=0时我们对应的不就是爬山法吗?,当p=1时,我们对应的就是蒙特卡洛(枚举)
1、在生成随机解的时候进行判断一下,当不满足的约束条件的时候之间再生成一个
第二种办法是加罚函数,当不满足约束条件时

这里就体现出来了模拟退火算法名字的来源,退火是温度随时间递减,但是这里我们Ct想要得到的是一个关于时间递增的函数所以我们这里就取了一下倒数。
这里的t怎么再编程中体现,很简单,这里的t我们可以看成迭代次数(循环)

另一个问题是什么时候停止搜索?
这里的准则并不唯一
1、我们可以设置达到指定的迭代次数,例如迭代200ci
2、达到指定的温度
3、我们找到最优解连续M(例如30次)次迭代都没有变化
%% 绘制函数图形
x = -3:0.1:3
y = 11*sin(x) + 7*cos(5*x);
figure(1);
plot(x, y,'b-')
% 不关闭图形,继续再上面画图
hold on
%% 参数初始化
narvs = 1;% 变量的个数
T0 = 100; % 初始的温度
T = T0; % 迭代中温度会发生变化,第一次迭代时温度就是T0
maxgen = 200; % 最大迭代次数
LK = 100; % 每个温度下的迭代次数
alfa = 0.95% 温度衰减系数
x_lb = -3; % x的下界
x_ub = 3; % x的上界
%% 随机生成一个初始解
x0 = x_lb + (x_ub - x_lb)*rand(1, narvs);
% scatter是绘制二维散点图的函数(这里返回h是为了获得函数的句柄,未来我们对其位置进行更新)
h = scatter(x0, Obj_fun1(x0), "*r");
%% 初始化用来保存中间结果的x和y的取值
iter_x = x0;
iter_y = Obj_fun1(x0);
%% 模拟退火过程
for iter = 1 : maxgen % 外循环,我们这里采用的是指定最大迭代次数
for i = 1 : LK % 内循环,在每个温度下开始迭代
title(['当前温度:', num2str(T)])
y0 = Obj_fun1(x0); % 计算当前解的函数值
disp('**********************************分割线********************************')
disp(['当前解的函数值:',num2str(y0)])
y = randn(1, narvs); % 生成一行narvs列的N(0,1)随机数
z = y / sqrt(sum(y .^ 2)) % 根据新解的产生规则计算x_new的值
x_new = x0 + z * T; % 根据新解的产生挥着计算z
% 如果这个新解的位置超出了定义域,就对其进行调整
for j = 1 : narvs
if x_new(j) < x_lb(j)
r = rand(1);
x_new(j) = r * x_lb(j) + (1 - r) * x0(j);
elseif x_new(j) > x_ub(j)
r = rand(1);
x_new(j) = r * x_ub(j) + (1 - r) * x0(j);
end
end
x1 = x_new; % 将调整后的x_new赋值给新解x1
y1 = Obj_fun1(x1); % 计算新解的函数值
disp(['新解的函数值:', num2str(y1)])
if y1 > y0 % 如果新解的函数值大于当前解的函数值
disp('更新当前解')
x0 = x1;
iter_x = [iter_x; x1];
iter_y = [iter_y; y1];
else
p = exp(-(y0 - y1) / T) % 根据MEtropolis准则计算一个概率
disp(['新解的函数值小于当前解的函数值,接受新解的概率为:', num2str(p)])
if rand(1) < p % 生成一个随机数和这个概率比较,如果该随机数小于这个概率
disp('该随机数小于这个概率,那么我们接受新解')
x0 = x1; % 更新当前解为新解
end
end
h.XData = x0; % 更新散点图句柄的x轴数据
h.YData = Obj_fun1(x0);
end
T = alfa*T; % 温度下降
pause(0.01) % 暂停一段时间(单位:秒)后再接着画图
end
其中用到的函数代码
function y = Obj_fun1(x)
y = 11*sin(x) + 7*cos(5*x);
end
模拟退火主函数
TSP问题(旅行商问题)
tic
% 清空一下
rng('shuffle')
clear
clc
%数据
coord = [11003.611100,42102.500000;11108.611100,42373.888900;11133.333300,42885.833300;11155.833300,42712.500000;11183.333300,42933.333300;11297.500000,42853.333300;11310.277800,42929.444400;11416.666700,42983.333300;11423.888900,43000.277800;11438.333300,42057.222200;11461.111100,43252.777800;11485.555600,43187.222200;11503.055600,42855.277800;11511.388900,42106.388900;11522.222200,42841.944400;11569.444400,43136.666700;11583.333300,43150.000000;11595.000000,43148.055600;11600.000000,43150.000000;11690.555600,42686.666700;11715.833300,41836.111100;11751.111100,42814.444400;11770.277800,42651.944400;11785.277800,42884.444400;11822.777800,42673.611100;11846.944400,42660.555600;11963.055600,43290.555600;11973.055600,43026.111100;12058.333300,42195.555600;12149.444400,42477.500000;12286.944400,43355.555600;12300.000000,42433.333300;12355.833300,43156.388900;12363.333300,43189.166700;12372.777800,42711.388900;12386.666700,43334.722200;12421.666700,42895.555600;12645.000000,42973.333300];
n = size(coord, 1); % 城市数量
figure % 新建一个窗口
plot(coord(:, 1), coord(:, 2), 'o')
hold on
d = zeros(n);
%% 初始化距离邻接矩阵
for i = 1 : n
for j = 1 : n
x1 = coord(i, 1);
y1 = coord(i, 2);
x2 = coord(j, 1);
y2 = coord(j, 2);
d(i, j) = sqrt((x1 - x2) ^ 2 + (y1 - y2) ^ 2);
end
end
%% 模拟退火初始化参数
T0 = 1000; % 初始化温度
T = T0; % 用于迭代的温度
maxgen = 1000; % 最大迭代次数
ingen = 500; % 每轮迭代的次数
alfa = 0.95; % 降温速率
%% 随机生成一个初始解
path0 = randperm(n);
res = cal(path0, d);
%% 定义保存中间过程的变量
min_res = res;
ans = (maxgen); % 保存每轮外层循环结束后的结果
%% 模拟退火过程
for i = 1 : maxgen
for j = 1 : ingen
new_path = GetNewPath(path0);
new_res = cal(new_path, d);
if(new_res < res)
path0 = new_path;
res = new_res;
else
p = exp(-(new_res - res) / T);
if(rand(1) < p)
path0 = new_path;
res = new_res;
end
end
if(res < min_res)
min_res = res;
best_path = path0;
end
end
ans(i) = min_res;
T = alfa * T;
end
disp('最佳的方案是:'); disp(mat2str(best_path))
disp('此时最优值是:'); disp(min_res)
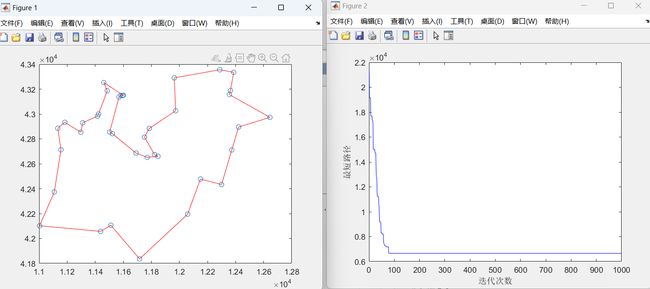
%% 作图
best_path = [best_path, best_path(1)]; % 因为我们最开始生成的是排列,求的是一个环,所以要加上第一个点
n = n + 1
for i = 1 : n - 1
j = i + 1;
a = best_path(i);
b = best_path(j);
x1 = coord(a, 1);
y1 = coord(a, 2);
x2 = coord(b, 1);
y2 = coord(b, 2);
plot([x1 x2], [y1, y2], '-r');
pause(0.02)
hold on
end
figure
plot(1:maxgen, ans, 'b-');
xlabel('迭代次数');
ylabel('最短路径');
toc % 用来记录程序完成的时间
小函数计算距离
function dist = cal(path, d)
n = length(path);
dist = 0;
for i = 1 : n - 1
dist = dist + d(path(i), path(i + 1));
end
dist = dist + d(path(n), path(1));
end
小函数生成新解
function res = GetNewpath(path0)
n = length(path0);
% 随机选择两种
p1 = 0.33; % 使用交换法产生新路径的概率
p2 = 0.33; % 使用移位法产生新路径的概率
r = rand(1); % 随机生成一个[0, 1]均匀分布的随机数
if r < p1 % 使用交换法产生新路径
c1 = randi(n); % 生成一个1-n的是随机整数
c2 = randi(n); % 生成一个1-n的是随机整数
res = path0;
res(c1) = path0(c2);
res(c2) = path0(c1);
elseif r < p1 + p2 % 使用移位法产生新路径
c1 = randi(n);
c2 = randi(n);
c3 = randi(n);
sort_c = sort([c1 c2 c3]);
c1 = sort_c(1); c2 = sort_c(2); c3 = sort_c(3);
tem1 = path0(1:c1 - 1);
tem2 = path0(c1 : c2);
tem3 = path0(c2 + 1 : c3);
tem4 = path0(c3 + 1 : n);
res = [tem1 tem2 tem3 tem4];
else % 使用倒置法产生新路径
c1 = randi(n);
c2 = randi(n);
if c1 > c2
tem = c2;
c2 = c1;
c1 = tem;
end
tem1 = path0(1 : c1 - 1);
tem2 = path0(c1 : c2);
tem3 = path0(c2 + 1 : end);
res = [tem1 fliplr(tem2) tem3];
end
end