【LeetCode热题100】打卡第39天：数组中第K个最大元素&最大正方形

【LeetCode热题100】打卡第39天：数组中第K个最大元素&最大正方形

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

博客主页：知识汲取者的博客

LeetCode热题100专栏：LeetCode热题100

Gitee地址：知识汲取者 (aghp) - Gitee.com

题目来源：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

数组中的第K个最大元素

题目

原题链接：215.数组中的第K个最大元素

题解

• 解法一：使用快速排序API

  import java.util.Arrays;
  import java.util.Collections;
  
  /**
   * @author ghp
   * @title
   * @description
   */
  class Solution {
      public int findKthLargest(int[] nums, int k) {
          Integer[] arr = Arrays.stream(nums).boxed().toArray(Integer[]::new);
          Arrays.sort(arr, Collections.reverseOrder());
          return arr[k - 1];
      }
  }
  

  复杂度分析：

  • 时间复杂度：最坏$O(n^2)$，最好$O(nlogn)$
  • 空间复杂度：$O(n)$，arr占用空间n，快排递归占用空间 logn，所以总的空间复杂度为 n

  其中 $n$ 为数组中元素的个数

  代码优化：

  class Solution {
      public int findKthLargest(int[] nums, int k) {
          Arrays.sort(nums);
          return nums[nums.length - k];
      }
  }
  

  复杂度分析：

  • 时间复杂度：最坏$O(n^2)$，最好$O(nlogn)$
  • 空间复杂度：$O(logn)$

  其中 $n$ 为数组中元素的个数

• 解法二：手动实现快速排序

  /**
   * @author ghp
   * @title
   * @description
   */
  class Solution {
      public int findKthLargest(int[] nums, int k) {
          return findKthLargestByQuickSort(nums, 0, nums.length - 1, k);
      }
  
      private int findKthLargestByQuickSort(int[] nums, int left, int right, int k) {
          if (left > right) {
              // 区间中没有元素，无法继续划分区间（根据题意，这里永不可达）
              return -1;
          }
          // 随机化选取主元
          int pivot = partition(nums, left, right);
          int result;
          if (k == pivot + 1) {
              // 第K大的元素是当前主元
              result = nums[pivot];
          } else if (k < pivot  + 1) {
              // 第K大的元素在主元左侧
              result = findKthLargestByQuickSort(nums, left, pivot - 1, k);
          } else {
              // 第K大的元素在主元右侧
              result = findKthLargestByQuickSort(nums, pivot + 1, right, k);
          }
          // 划分右侧子区间
          return result;
      }
  
      private int partition(int[] nums, int left, int right) {
          int pivot = nums[right];
          int i = left - 1;
          // 根据主元将数组划分为左右子数组（左侧子数组>主元，右侧子数组<=主元）
          for (int j = left; j < right; j++) {
              if (nums[j] > pivot) {
                  // 将比主元大的元素放到 i+1 的左侧
                  swap(nums, ++i, j);
              }
          }
          // 将主元放到分界点，然后返回主元索引
          swap(nums, ++i, right);
          return i;
      }
  
      private void swap(int[] nums, int i, int j) {
          int temp = nums[i];
          nums[i] = nums[j];
          nums[j] = temp;
      }
  }
  

  复杂度分析：

  • 时间复杂度：最坏$O(n^2)$，最好$O(nlogn)$
  • 空间复杂度：$O(logn)$

  其中 $n$ 为数组中元素的个数

  代码优化：时间复杂度优化

  由于快速排序是不稳定的，最好的情况$O(n^2)$，最坏的情况是$nlogn$，为了提高快排的稳定性，我们可以引入一个随机因子，使得时间复杂度的期望值接近于$O(n)$，这个快排是最基本的算法，这里不做过多介绍了，感兴趣的可以参考我的另一篇文章：详解十大排序算法，这篇文章详细介绍了 十大排序算法的思路、实现，还有十分详细的图解

  import java.util.Random;
  
  /**
   * @author ghp
   * @title
   * @description
   */
  class Solution {
      public int findKthLargest(int[] nums, int k) {
          return findKthLargestByQuickSort(nums, 0, nums.length - 1, k);
      }
  
      private int findKthLargestByQuickSort(int[] nums, int left, int right, int k) {
          if (left > right) {
              // 区间中没有元素，无法继续划分区间（根据题意，这里永不可达）
              return -1;
          }
          // 随机化选取主元
          int pivot = randomPartition(nums, left, right);
          int result;
          if (k == pivot + 1) {
              // 第K大的元素是当前主元
              result = nums[pivot];
          } else if (k < pivot + 1) {
              // 第K大的元素在主元左侧
              result = findKthLargestByQuickSort(nums, left, pivot - 1, k);
          } else {
              // 第K大的元素在主元右侧
              result = findKthLargestByQuickSort(nums, pivot + 1, right, k);
          }
          // 划分右侧子区间
          return result;
      }
  
      private int randomPartition(int[] nums, int left, int right) {
          // 从子区间中随机选取一个元素作为主元
          Random random = new Random();
          int nonce = random.nextInt(right - left + 1) + left;
          swap(nums, nonce, right);
          int pivot = nums[right];
          int i = left - 1;
          // 根据主元将数组划分为左右子数组（左侧子数组>主元，右侧子数组<=主元）
          for (int j = left; j < right; j++) {
              if (nums[j] > pivot) {
                  // 将比主元大的元素放到 i+1 的左侧
                  swap(nums, ++i, j);
              }
          }
          // 将主元放到分界点，然后返回主元索引
          swap(nums, ++i, right);
          return i;
      }
  
      private void swap(int[] nums, int i, int j) {
          int temp = nums[i];
          nums[i] = nums[j];
          nums[j] = temp;
      }
  }
  

• 解法三：堆排序

最大正方形

题目

原题链接：221.最大正方形

题解

• 解法一：向下扩展

  本题思路可以参考这题：【LeetCode热题100】打卡第26天：最大矩形

  两者是类似的题目，这题相较于 最大矩形 哪一题多了一个限制，那就是长要等于宽。这里就不多做讲解了 (●ˇ∀ˇ●)

  PS：我感觉很离谱，前面那一题比这一题限制要少，但却是困难提，这一题限制多反而是中等题，不知道LeetCode是怎么划分题目难度的，我表示很疑惑

  

  

  /**
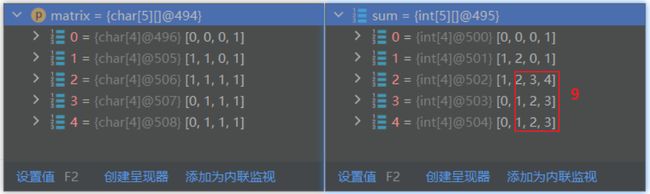
   * @author ghp
   * @title
   * @description
   */
  class Solution {
      public int maximalSquare(char[][] matrix) {
          int row = matrix.length;
          int col = matrix[0].length;
          // 构建width数组
          int[][] sum = new int[row][col];
          for (int i = 0; i < row; i++) {
              for (int j = 0; j < col; j++) {
                  if (matrix[i][j] == '1') {
                      if (j == 0) {
                          sum[i][j] = 1;
                      } else {
                          sum[i][j] += sum[i][j - 1] + 1;
                      }
                  } else {
                      sum[i][j] = 0;
                  }
              }
          }
          int ans = 0;
          // 枚举每一个节点
          for (int i = 0; i < row; i++) {
              for (int j = 0; j < col; j++) {
                  int width = sum[i][j];
                  // 枚举当前节点下的所有行
                  for (int k = i; k < row; k++) {
                      int height = k - i + 1;
                      if (sum[k][j] < height || height > width) {
                          // 出现断层 || 高已经超过当前宽度
                          break;
                      }
                      // 更新正方形的宽（正方形的面积受限于当前已遍历层中的最小宽）
                      width = Math.min(width, sum[k][j]);
                      // 更新最大矩形的面积（正方形的面积受限于长和宽）
                      int t = Math.min(width, height);
                      ans = Math.max(ans, t * t);
                  }
              }
          }
          return ans;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^2\ast m)$
  • 空间复杂度：$O(n\ast m)$

  其中 $n$ 为数组的行，$m$为数组的列

  可以看到，时间复杂度虽然比较高，但是却能过，这是因为我们通过if (sum[k][j] < height || height > width)提前剔除了大量不必要的计算（起到了类似于剪枝的效果），从而使得加速计算出结果

• 解法二：往上扩展

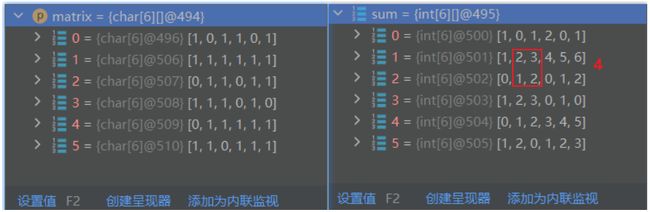
  解法一，自上而下枚举，节点要枚举两遍，第一遍枚举构建sum数组，第二遍枚举计算节点能构成矩形的最大面积。我们可以换一种思路，自下而上枚举，在枚举节点构建sum数组的同时，还计算当前节点能构成矩形的最大面积，这样就能够省掉一遍枚举，虽然时间复杂度没有减小，但是节约了时间

  PS：同样的，也是参考之前最大矩形这题写的，不是很理解的可以回看，前面最大矩形那一题进行了详细的详解，有图有分析，可以说是手把手教学

  /**
   * @author ghp
   * @title
   * @description
   */
  class Solution {
      public int maximalSquare(char[][] matrix) {
          int row = matrix.length;
          int col = matrix[0].length;
          int[][] sum = new int[row][col];
          int ans = 0;
          for (int i = 0; i < row; i++) {
              // 构建sum数组
              for (int j = 0; j < col; j++) {
                  if (matrix[i][j] == '1') {
                      if (j == 0) {
                          sum[i][j] = 1;
                      } else {
                          sum[i][j] += sum[i][j - 1] + 1;
                      }
                  } else {
                      sum[i][j] = 0;
                  }
                  int width = sum[i][j];
                  // 以当前节点为矩形的右下角，往上枚举
                  for (int k = i; k >= 0; k--) {
                      int height = i - k + 1;
                      if (sum[k][j] < height || height > width) {
                          // 出现断层 || 高已经超过当前宽度
                          break;
                      }
                      // 更新正方形的宽（正方形的面积受限于当前已遍历层中的最小宽）
                      width = Math.min(width, sum[k][j]);
                      // 更新最大矩形的面积（正方形的面积受限于长和宽）
                      int t = Math.min(width, height);
                      ans = Math.max(ans, t * t);
                  }
              }
          }
          return ans;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^2\ast m)$
  • 空间复杂度：$O(n\ast m)$

  其中 $n$ 为数组的行，$m$为数组的列

• 解法三：动态规划

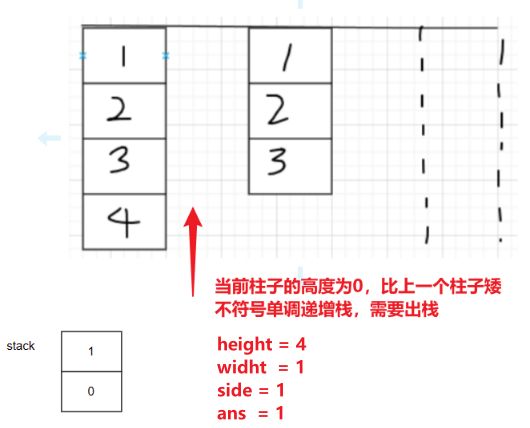
• 解法四：单调栈

  其实本题也是参考我前面写的那一题，这里再重新讲解一下本题的思路（现在思路是有，但是代码还有有一点写不出┭┮﹏┭┮）

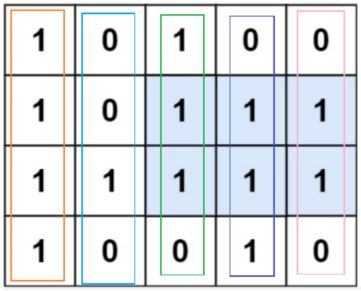
  1. 构建sum数组，sum数组就是纵向求和

     

     

     2. 一层一层的遍历数组，把当前层看着一个地平线

        比如第一层：

        

        我们在遍历第一层的同时将柱子不断加入栈中，保证栈是严格单调递增的，因为只有保持栈中柱子是单调递增，我们才能够确定左边界（左边矮，右边高，自然左侧柱子就是左边界）

        

        

        不断迭代，最终我们就可以得到最大正方形的面积

  import java.util.ArrayDeque;
  import java.util.Deque;
  
  /**
   * @author ghp
   * @title
   * @description
   */
  class Solution {
      public int maximalSquare(char[][] matrix) {
          int row = matrix.length;
          int col = matrix[0].length;
          // 构建sum数组
          int[][] sum = new int[row + 1][col + 1];
          for (int i = 1; i <= row; i++) {
              for (int j = 1; j <= col; j++) {
                  sum[i][j] = matrix[i - 1][j - 1] == '0' ? 0 : sum[i - 1][j] + 1;
              }
          }
          // 遍历每一层的柱子，更新max
          int ans = Integer.MIN_VALUE;
          for (int i = 1; i <= row; i++) {
              // 更新正方形的最大面积
              ans = Math.max(ans, largestSquareArea(sum[i]));
          }
          return ans;
      }
  
      private int largestSquareArea(int[] heights) {
          // 创建一个临时数组，前0用于计算第一个柱子的面积，后一个0用于强制出栈（这一步超级重要）
          int[] tempArr = new int[heights.length + 2];
          for (int i = 1; i < heights.length + 1; i++) {
              tempArr[i] = heights[i - 1];
          }
          // 递增栈（栈中存储柱子的索引号，栈中的柱子的高度严格递增）
          Deque<Integer> stack = new ArrayDeque<>();
          int ans = 0;
          for (int i = 0; i < tempArr.length; i++) {
              while (!stack.isEmpty() && tempArr[i] < tempArr[stack.peek()]) {
                  // 当前柱子的右边界已确定，可以计算已弹出柱子的面积
                  int height = tempArr[stack.poll()];
                  int width =  i - stack.peek() - 1;
                  int side = Math.min(height, width);
                  ans = Math.max(ans, side * side);
              }
              stack.push(i);
          }
          return ans;
      }
  }
  

  代码优化：

  这段代码是我叫ChartGPT对上面代码进行的一个优化，我也是试一试，没想到他还真给我优化了，这人工智能是真的牛，可能我没有想到这样子写，但是这个代码还是能够看的懂的，优化前我们通过自上而下遍历数组构建sum数组，但是发现矩形的最大面积的更新只跟当前层有关，与下一层无关，所以我们可以在构建sum数组的同时利用单调栈去更新当前最大正方形的面积。这里优化思路和前面的 往下扩展==>往上扩展 是一样的，都是在构建sum数组的时候更新最大正方形的面积，我相信只要看懂优化前的代码，优化后的代码也是很容易能够看懂的，至于能否写出这么优雅的代码，就需要不但的积累和练习了，优雅不是一蹴而就的，需要不断积累，正如我刷题专栏上写的铭言：不积硅步无以至千里，不积小流无以至千里。天赋这东西不得不承认他是存在的，但是这东西不是我所能决定的，后期的努力我所能决定的，我是坚信能够勤能补拙的，不渴望能够媲美那些天赋型选手，只希望能战胜和我差不多的选手，加油(ง •_•)ง

  public int maximalSquare(char[][] matrix) {
      int rows = matrix.length;
      int cols = matrix[0].length;
      int[] heights = new int[cols + 1]; // 高度数组，最后一个元素为0
      
      int maxArea = 0;
      Deque<Integer> stack = new ArrayDeque<>(); // 单调栈，存放柱子的下标
      
      for (int i = 0; i < rows; i++) {
          // 构建柱状图，更新每一列的高度
          for (int j = 0; j < cols; j++) {
              if (matrix[i][j] == '1') {
                  heights[j]++;
              } else {
                  heights[j] = 0;
              }
          }
          
          stack.clear();
          
          // 计算每个柱子的面积
          for (int j = 0; j <= cols; j++) {
              while (!stack.isEmpty() && heights[j] < heights[stack.peek()]) {
                  // 当前柱子的右边界已确定，可以计算已弹出柱子的面积
                  int height = heights[stack.pop()];
                  int width = stack.isEmpty() ? j : (j - stack.peek() - 1);
                  int side = Math.min(height, width);
                  maxArea = Math.max(maxArea, side * side);
              }
              stack.push(j);
          }
      }
      
      return maxArea;
  }