数据结构 特殊线性表---栈、队列、串
总括:从数据结构角度看,栈和队列是操作受限的线性表,他们的逻辑结构相同;串是重要的非数值处理对象,它是以字符作为数据元素的线性表。
栈
定义
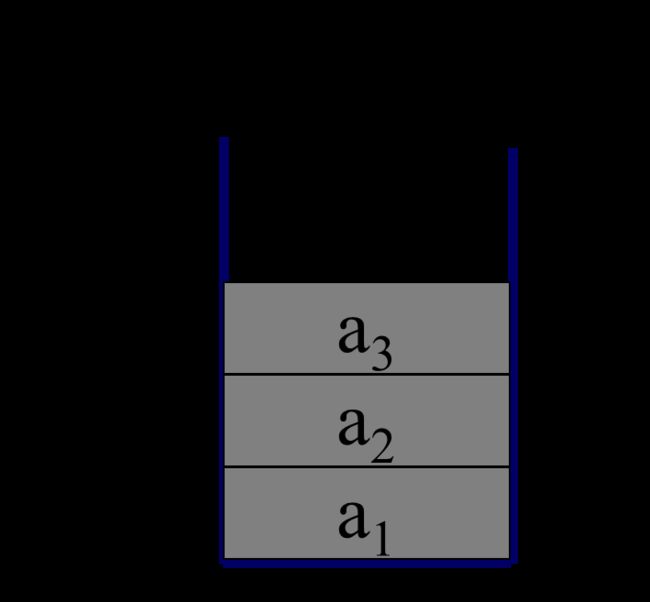
限定仅在表尾进行插入和删除操作的线性表
允许插入删除的一端称为栈顶,另一端为栈底
插入:入栈、进栈、压栈 删除:出栈、弹栈
注:栈只是对表插入和删除操作的位置进行了限制,并没有限定插入和删除操作进行的时间
顺序栈
//入栈
void seqStack::Push ( T x)
{
if (top==MAX_SIZE-1) throw “溢出”;
top++;
data[top]=x;
}
//出栈
int seqStack:: Pop ( )
{
if (top==-1) throw “溢出”;
x=data[top--];
return x;
}
链栈
//压栈 没有栈满问题
void LinkStack::Push(T x)
{
s=new Node;
s->data=x;
s->next=top;
top=s;
}
//出栈
int LinkStack::Pop( )
{
if (top==NULL)
throw "下溢";
x=top->data;
p=top;
top=top->next;
delete p;
return x;
}
顺序栈和链栈的比较
时间性能:均为O(1)
空间性能: 顺序栈:有元素个数限制和空间浪费问题
链栈:没有栈满的问题,只有当内存没有可用空间时才会出现栈满,但是每个元 素都需要一个指针域,从而产生了结构性开销
结:元素个数变化较大时用链栈,反之,用顺序栈
队列
定义
只允许在一端进行插入操作,而另一端进行删除操作的线性表
允许插入(也称入队、进队)的一端称为队尾,允许删除(也称出队)的一端称为队头
操作特性:先进先出
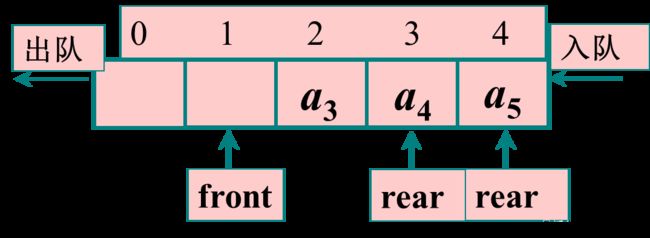
顺序队列
入队操作时间性能为O(1)
假溢出:当元素被插入到数组中下标最大的位置上之后,队列的空间用尽,但此时数组的低端还 有空闲空间,如下图
//入队
void CirQueue::EnQueue(T x)
{
if ((rear+1) % QueueSize ==front) throw "上溢";
rear=(rear+1) % QueueSize;
data[rear]=x;
}
//出队
int CirQueue::DeQueue( )
{
if (rear==front) throw "下溢";
front=(front+1) % QueueSize;
return data[front];
}
//读队头元素
int CirQueue::GetQueue( )
{
if (rear==front) throw "下溢";
i=(front+1) % QueueSize;
return data[i];
}
链队列
队头指针为链表的头指针
入队:
//入队
void LinkQueue::EnQueue(T x)
{
s=new Node;
s->data=x;
s->next=NULL;
rear->next=s;
rear=s;
}
//出队
int LinkQueue::DeQueue( )
{
if (rear==front) throw "下溢";
p=front->next;
x=p->data;
front->next=p->next;
if (p->next==NULL) rear=front;
delete p;
return x;
}
串
定义
零个或多个字符组成的有限序列
主串: 包含子串的串
子串: 串中任意个连续的字符组成的子序列
子串的位置: 子串的第一个字符在主串中的序号
串的比较:通过组成串的字符之间的编码比较进行
给定两个串:X="x1x2… xn"和Y="y1y2… ym",则:
1. X=Y: n=m 且x1=y1,…,xn = ym
2. X<Y,其一成立即可:
⑴ n<m 且 xi=yi(1≤ i≤n)
⑵存在k ≤ min(m,n),使得xi=yi(1≤i≤k-1)且xk<yk
常用函数:
⑴ StrLength (s):求长度
⑵ StrAssign (s1, s2):赋值,将s2的值赋值给串s1
⑶ StrConcat (s1, s2, s):连接,将串s2放在串s1的后面连接成一个新串s
⑷ SubStr (s, i, len):求子串,返回从串s的第i个字符开始取长为 len 的子串
⑸ StrCmp (s1, s2):串比较,若s1=s2,返回0;若s1
⑹ StrIndex (s, t):定位,返回子串t在主串s中首次出现的位置。若t不是s的子串,则返回0
⑺ StrInsert (s, i, t):插入,将串t插入到串s中的第i个位置
⑻ StrDelete (s, i, len):删除,在串s中删除从第i个字符开始的连续len个字符
⑼ StrRep (s, t, r):替换,在串s中用串r替换所有与串t相等的子串
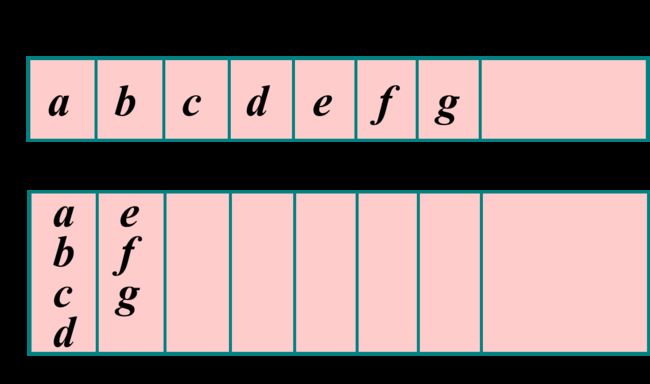
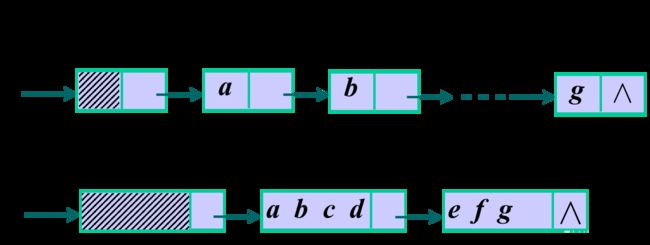
存储结构
顺序串:用数组存储
链接串:用链式存储结构存储
前中后缀表达式转换
例:已知中缀表达式a+b*c-(d+e),将其转换为前后缀表达式
1.按照运算符的优先级对所有的运算单位加括号 式子变成 ((a+(b*c))-(d+e))
2.转换前缀与后缀表达式
①前缀表达式:把运算符号移动到对应的括号前面变成 -( +(a *(bc)) +(de))
去掉括号 -+a*bc+de
②后缀表达式:把运算符号移动到对应的括号后面变成 ((a(bc)* )+ (de)+ )-
去掉括号 abc*+de+-
模式匹配
给定主串S、模式串T,在S中寻找T 的过程称为模式匹配
匹配成功,返回T在S中的位置;匹配失败,返回0
BT算法
1. 在串S和串T中设比较的起始下标i和j;
2. 循环直到S或T的所有字符均比较完;
2.1 如果S[i]=T[j],继续比较S和T的下一个字符;
2.2 否则,将i和j回溯,准备下一趟比较;
3. 如果T中所有字符均比较完,匹配成功,返回匹配的起始比较下标;否则,匹配失败,返回0;
int BF(char S[ ], char T[ ])
{
i=1; j=1;
while (i<=S[0]&&j<=T[0])
{
if (S[i]==T[j]) {
i++; j++;
}
else {
i=i-j+2; j=1;
}
}
if (j>T[0]) return (i-j+1);
else return 0;
}
KMP算法
1.在串S和串T中分别设比较的起始下标i和j;2. 循环直到S中所剩字符长度小于T的长度或T中所有字符均比较完毕
2.1 如果S[i]=T[j],继续比较S和T的下一个字符;否则
2.2 将j向右滑动到next[j]位置,即j=next[j];
2.3 如果j=0,则将i和j分别加1,准备下一趟比较;
3. 如果T中所有字符均比较完毕,则返回匹配的起始下标;否则返回0;
void GetNext(char T[ ], int next[ ])
{
next[1]=0; j=1; k=0;
while (j定义j = 1 时,k = 0
j = 2,k = 1
j = 3, a 前面子串ab的前缀a和后缀b不匹配,k = 1
j = 4, a 前面子串aba的前缀ab和后缀ba不匹配,但前缀a和后缀a匹配成功,k = 1+1
j = 5, b 前面子串abaa存在前缀a和后缀a匹配,k = 1+1
j = 6, c 前面子串abaab存在前缀ab和后缀ab匹配,k = 1+2 (1为开始存在的,2为匹配元素ab的长度)
j = 7, a 前面子串abaabc无前缀后缀匹配,k = 1
j = 8, c 前面子串abaabca存在前缀a和后缀a匹配,k = 1+1