数据分析之Numpy

1. Anaconda安装

Anaconda就是可以便捷获取包且对包能够进行管理，同时对环境可以统一管理的发行版本。Anaconda包含了conda、Python在内的超过180个科学包及其依赖项。

官网：https://www.anaconda.com/

安装一直点击Next

选择安装路径：

提示：出现警告，路径中含有空格，anaconda可能会出现问题！

那我们就换一个不包含空格和中文的安装路径！

选中勾选，点击Install

安装完成！

下一步，配置环境变量。

在Path中添加，

F:\environment\anaconda\Scripts  (conda自带脚本)
F:\environment\anaconda  (python需要)
F:\environment\anaconda\Library\bin  (jupyter notebook动态库)

验证是否安装成功，命令行输入python，看是否能够进行python命令

退出命令行，输入jupyter notebook，看是否可以正常运行

如果发现安装的anaconda中的python版本太高，我们可以降低python的版本

搜索打开anaconda prompt

输入命令

conda install python=3.8

如果在执行回退python版本的命令时出现了报错或者是其他问题的话，一般就是因为镜像源所导致，设置一下conda镜像源就好，命令如下：

# 查看版本
conda -V
# 更新conda环境
conda update -n base conda
# 更新conda的所有包
conda update --all

conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/
conda config --set show_channel_urls yes

---

2. juypter

Jupyter Notebook 的本质是一个 Web 应用程序，便于创建和共享程序文档，支持实时代码，数学方程，可视化和 markdown。 用途包括：数据清理和转换，数值模拟，统计建模，机器学习等等。

Jupyter Notebook的主要特点：

• 编程时具有语法高亮、缩进、tab补全的功能。
• 可直接通过浏览器运行代码，同时在代码块下方展示运行结果。
• 以富媒体格式展示计算结果。富媒体格式包括：HTML，LaTeX，PNG，SVG等。
• 对代码编写说明文档或语句时，支持Markdown语法。
• 支持使用LaTeX编写数学性说明。

在命令窗口输入命令，启动jupyter：

jupyter notebook

jupyter常用快捷键：

Enter：进入edit模式
Esc：进入command模式
H：展示快捷键帮助 ：这是个好技能，不知道的时候点一点。
A：在上方增加一个cell
B：在下方增加一个cell
X：剪切该cell
C：复制该cell
V：在该cell下方粘贴复制的cell
Shift-V：在该cell上方粘贴复制的cell
L：隐藏、显示当前cell的代码行号
shift-L：隐藏/显示所有cell的代码行号
O：隐藏该cell的output
DD：删除这个cell
Z：撤销删除操作
Y：转为code模式
M：转为markdown模式
R：转为raw模式
Shift-Enter：运行本单元，选中下个单元 新单元默认为command模式
Ctrl-Enter 运行本单元
Alt-Enter 运行本单元，在其下插入新单元 新单元默认为edit模式
OO：重启当前kernal
II：打断当前kernal的运行
shift+上/下：向上/下选中多个代码块
上/下：向上/下选中代码块
F：查找替换
Tab：代码补全
ctrl]或Tab：缩进（向右）
ctrl[或shift-Tab：反缩进（向左）
ctrl A：全选
ctrl D：删除整行
ctrl Z：撤销

---

3. numpy简介

NumPy(Numerical Python) 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。

NumPy 的前身 Numeric 最早是由 Jim Hugunin 与其它协作者共同开发，2005 年，Travis Oliphant 在 Numeric 中结合了另一个同性质的程序库 Numarray 的特色，并加入了其它扩展而开发了 NumPy。NumPy 为开放源代码并且由许多协作者共同维护开发。

NumPy 是一个运行速度非常快的数学库，主要用于数组计算，包含：

• 一个强大的N维数组对象 ndarray
• 广播功能函数
• 整合 C/C++/Fortran 代码的工具
• 线性代数、傅里叶变换、随机数生成等功能

为什么使用numpy？

• 快速，简洁，对于同样的数值计算任务，使用Numpy要不直接编写Python代码更加的便捷；

• Numpy中的数组的存储效率和输入输出性能均优于Python中等价的基本数据结构；

• Numpy的大部分代码是使用C语言编写的，底层算法在设计上有着优异的性能，使得Numpy更加的高效。

---

4. numpy数组

4.1 ndarray对象

NumPy 最重要的一个特点是其 N 维数组对象 ndarray，它是一系列同类型数据的集合，以 0 下标为开始进行集合中元素的索引。

ndarray 对象是用于存放同类型元素的多维数组。

ndarray 中的每个元素在内存中都有相同存储大小的区域。

ndarray 内部由以下内容组成：

• 一个指向数据（内存或内存映射文件中的一块数据）的指针。
• 数据类型或 dtype，描述在数组中的固定大小值的格子。
• 一个表示数组形状（shape）的元组，表示各维度大小的元组。
• 一个跨度元组（stride），其中的整数指的是为了前进到当前维度下一个元素需要"跨过"的字节数。

属性：

属性	说明
ndarray.ndim	秩，即轴的数量或维度的数量
ndarray.shape	数组的维度，对于矩阵，n 行 m 列
ndarray.size	数组元素的总个数，相当于 .shape 中 n*m 的值
ndarray.dtype	ndarray 对象的元素类型
ndarray.itemsize	ndarray 对象中每个元素的大小，以字节为单位
ndarray.flags	ndarray 对象的内存信息
ndarray.real	ndarray元素的实部
ndarray.imag	ndarray 元素的虚部
ndarray.data	包含实际数组元素的缓冲区，由于一般通过数组的索引获取元素，所以通常不需要使用这个属性。

4.2 array创建数组

numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)

名称	描述
object	数组或嵌套的数列
dtype	数组元素的数据类型，可选
copy	对象是否需要复制，可选
order	创建数组的样式，C为行方向，F为列方向，A为任意方向（默认）
subok	默认返回一个与基类类型一致的数组
ndmin	指定生成数组的最小维度

# array()函数
np.array([1,3,5,7,8])

# 元组
np.array((1,3,5,6,7,8))

# 数组
a = np.array([1,4,5,7,8])
np.array(a)

# 迭代对象  range(10)是从0~9
np.array(range(10))

# 生成器
np.array([i**2 for i in range(10)])

**练习：创建10以内的偶数的数组 **

np.array([i for i in range(0,10,2)])

np.array([i for i in range(10) if i%2==0])

1.当列表中元素类型不同时，同时含有数值型和字符型时，会将值全部转化为字符型，如

# 列表中元素类型不同
np.array([1,2,3,4,'5'])

2.当列表中同时含有整型和浮点型时，会将值全部转化为浮点型，如

# 整型和浮点型
np.array([1,2,3,4,5.7,6.8])

3.二维数组：嵌套序列（列表和元组均可），但是必须保证嵌套序列中元素数量相同，如：

# 二维数组：嵌套序列（列表和元组均可）
np.array([[1,2,4],('3','5','6')])

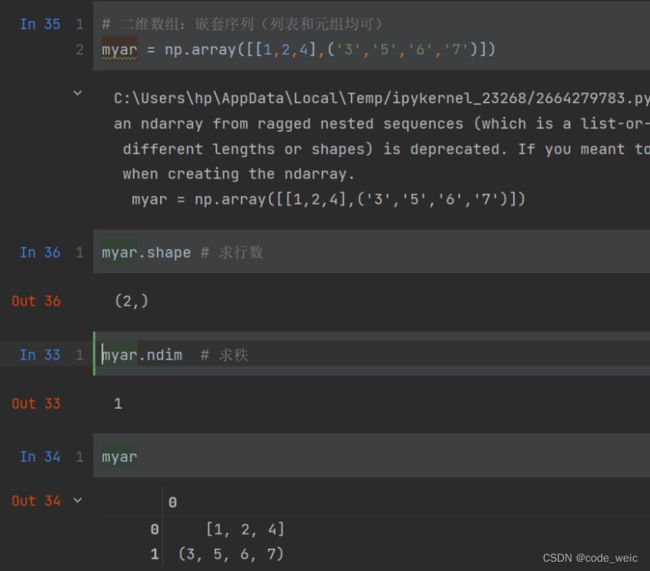
4.当嵌套序列中元素数量不相同时，会强制转化为一维，如

# 二维数组：嵌套序列（列表和元组均可）
myar = np.array([[1,2,4],('3','5','6','7')])
myar.shape # 求行数
myar.ndim  # 求秩
myar

numpy.arrray参数详解

• dtype

  设置dtype参数，默认自动识别

  将整型设置为浮点型，如

  np.array([1,1,2,3,4],dtype=float)
  

  

  将浮点型设置为整型，会直接向下取整，如

  np.array([1.2,4.6,7.5,3.8],dtype=int)
  

  

• copy

  设置copy参数，默认为true

  使用b=np.array(a)，是值传递，当b中的值发生改变时，a中的值不会发生变化

  

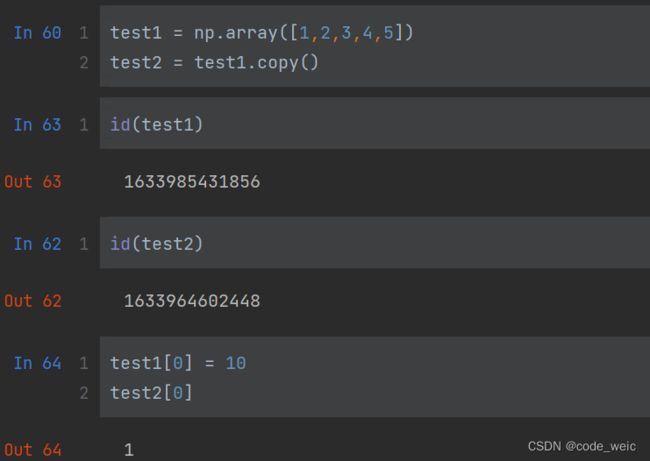
  使用直接等于，b=a，是引用赋值，当b中的值改变时，a中的值也会随之变化

  

  使用copy方式时，与b=np.array(a)效果相同

  test1 = np.array([1,2,3,4,5])
  test2 = test1.copy()
  

  test1与test2的地址空间不同，test1中的值发生改变时，不会影响到test2中的值

  

• ndmin用于指定数组的维度

  将一维变为三维

  np.array([1,2,3],ndmin=3)
  

  

• subok

  类型为布尔值，默认为False。False：使用object数组的数据类型；True：使用object的内部数据类型

  # 创建一个矩阵
  a = np.mat([1,2,3,4])
  print(type(a))
  
  # 既要复制一份副本，又要保持原类型
  at = np.array(a,subok=True)
  af = np.array(a,subok=False)
  print('at,subok为true: ',type(at))
  print('af,subok为false: ',type(af))
  

  

4.3 arange区间数组

从数值范围创建数组

numpy.arange(start, stop, step, dtype)

参数	描述
start	起始值，默认为0
stop	终止值（不包含）
step	步长，默认为1
dtype	返回ndarray的数据类型，如果没有提供，则会使用输入数据的类型。

如果为浮点型，则

可以使用dtype属性来指定类型，如

c = np.arange(5,dtype=float)

题目：

在庆祝教师节活动中，学校为了烘托节日气氛，在200米长的校园主干道一侧，从起点开始，每间隔3米插一面彩旗，由近到远排成一排，问：

1.最后一面彩旗会插到终点处吗？

2.一共插多少面彩旗？

res = np.arange(0,201,3)

res.size # len(res) 也可以，因为是一维的

如何防止Float不精确影响numpy.arange？

注意：cell((stop - start)/step)确定项目数，小浮点不精确(stop=.400000001)可以向列表中添加意外值。

想得到一个长度为3的、从0.1开始的、间隔为0.1的数组，想当然地如下coding，结果意料之外：

4.4 linspace等差数列

numpy.linspace 函数用于创建一个一维数组，数组是一个等差数列构成的，格式如下：

np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

参数	描述
start	序列的起始值
stop	序列的终止值，如果endpoint为true，该值包含于数列中
num	要生成的等步长的样本数量，默认为50
endpoint	该值为 true 时，数列中包含stop值，反之不包含，默认是True。
retstep	如果为 True 时，生成的数组中会显示间距，反之不显示。
dtype	ndarray 的数据类型

# 起始点为1  终止点为10  数列个数为10
np.linspace(1,10,10)

# 使用等差数列 实现输出0 0.5 1 1.5 2 2.5 3 3.5 4
np.linspace(0,4,9)

# 设置起始值为2.0  终点值为3.0  数列个数为5
np.linspace(2.0,3.0,num=5)

# 设置参数endpoint 为False时，不包含终止值
np.linspace(2.0,3.0,num=5,endpoint=False)

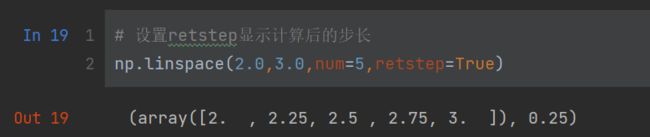
# 设置retstep显示计算后的步长
np.linspace(2.0,3.0,num=5,retstep=True)

# 想得到一个长度为10的、从0.1开始的、间隔为0.1的数组
np.linspace(0.1,1,10)

等差数列，在线性回归中经常作为样本集

如：生成x_data，值为[0,100]之间500个等差数列数据集合作为样本特征，根据目标线性方程$\ y=3x+2\ $，生成相应的标签集合y_data。

x_data = np.linspace(0,100,500)
x_data

4.5 logspace等比数列

numpy.logspace 函数用于创建一个于等比数列。格式如下：

np.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None)

参数	描述
start	序列的起始值为：base ** start
stop	序列的终止值为：base ** stop。如果endpoint为true，该值包含于数列中
num	要生成的等步长的样本数量，默认为50
endpoint	该值为 true 时，数列中中包含stop值，反之不包含，默认是True。
base	对数 log 的底数。base值默认为10.
dtype	ndarray 的数据类型

a = np.logspace(0,9,10,base=2)  # 从2的0次方开始，到2的9次方结束，分成10等份
a

练习题

一个穷人到富人那里去借钱，原以为富人不愿意，哪知富人一口答应了下来，但提出了条件：

• 在30天中，富人第一天只借给穷人1万元，第二天借给2万元，以后每天所借的钱数都比上一天的多一万

• 但借钱的第一天，穷人还1分钱，第二天还2分钱，以后每天还的钱数都是上一天的两倍。

• 30天后互不相欠

穷人听后觉得挺划算，本想定下来，但又想到富人是个吝啬出了名的，怕上当，所以很为难。计算出确认是否向富人借钱 。

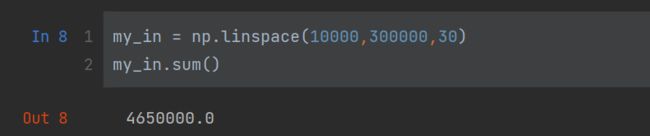
my_in = np.linspace(10000,300000,30)
my_in.sum()

my_out = np.logspace(0,29,num=30,base=2)
my_out

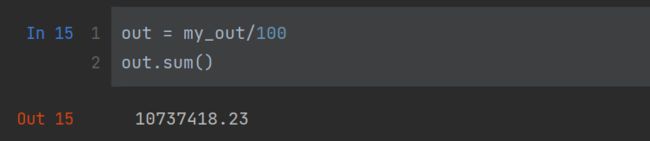
out = my_out/100
out.sum()

if my_in.sum()>out.sum():
    print("借钱")
else:
    print("不借钱")

4.6 numpy.empty

numpy.empty 方法用来创建一个指定形状（shape）、数据类型（dtype）且未初始化的数组：

numpy.empty(shape, dtype = float, order = 'C')

参数	描述
shape	数组形状
dtype	数据类型，可选
order	有"C"和"F"两个选项,分别代表，行优先和列优先，在计算机内存中的存储元素的顺序。

例：

import numpy as np 
x = np.empty([3,2], dtype = int) 
print (x)

4.7 numpy.zeros

创建指定大小的数组，数组元素以 0 来填充：

numpy.zeros(shape, dtype = float, order = 'C')

参数	描述
shape	数组形状
dtype	数据类型，可选
order	‘C’ 用于 C 的行数组，或者 ‘F’ 用于 FORTRAN 的列数组

例：

import numpy as np
 
# 默认为浮点数
x = np.zeros(5) 
print(x)
 
# 设置类型为整数
y = np.zeros((5,), dtype = int) 
print(y)
 
# 自定义类型
z = np.zeros((2,2), dtype = [('x', 'i4'), ('y', 'i4')])  
print(z)

4.8 numpy.ones

创建指定形状的数组，数组元素以 1 来填充：

numpy.ones(shape, dtype = None, order = 'C')

参数	描述
shape	数组形状
dtype	数据类型，可选
order	‘C’ 用于 C 的行数组，或者 ‘F’ 用于 FORTRAN 的列数组

例：

import numpy as np
 
# 默认为浮点数
x = np.ones(5) 
print(x)
 
# 自定义类型
x = np.ones([2,2], dtype = int)
print(x)

4.9 numpy.zeros_like

numpy.zeros_like 用于创建一个与给定数组具有相同形状的数组，数组元素以 0 来填充。

numpy.zeros 和 numpy.zeros_like 都是用于创建一个指定形状的数组，其中所有元素都是 0。

它们之间的区别在于：numpy.zeros 可以直接指定要创建的数组的形状，而 numpy.zeros_like 则是创建一个与给定数组具有相同形状的数组。

numpy.zeros_like(a, dtype=None, order='K', subok=True, shape=None)

参数	描述
a	给定要创建相同形状的数组
dtype	创建的数组的数据类型
order	数组在内存中的存储顺序，可选值为 ‘C’（按行优先）或 ‘F’（按列优先），默认为 ‘K’（保留输入数组的存储顺序）
subok	是否允许返回子类，如果为 True，则返回一个子类对象，否则返回一个与 a 数组具有相同数据类型和存储顺序的数组
shape	创建的数组的形状，如果不指定，则默认为 a 数组的形状。

例：

import numpy as np
 
# 创建一个 3x3 的二维数组
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
 
# 创建一个与 arr 形状相同的，所有元素都为 0 的数组
zeros_arr = np.zeros_like(arr)
print(zeros_arr)

4.10 numpy.ones_like

numpy.ones_like 用于创建一个与给定数组具有相同形状的数组，数组元素以 1 来填充。

numpy.ones 和 numpy.ones_like 都是用于创建一个指定形状的数组，其中所有元素都是 1。

它们之间的区别在于：numpy.ones 可以直接指定要创建的数组的形状，而 numpy.ones_like 则是创建一个与给定数组具有相同形状的数组。

numpy.ones_like(a, dtype=None, order='K', subok=True, shape=None)

参数	描述
a	给定要创建相同形状的数组
dtype	创建的数组的数据类型
order	数组在内存中的存储顺序，可选值为 ‘C’（按行优先）或 ‘F’（按列优先），默认为 ‘K’（保留输入数组的存储顺序）
subok	是否允许返回子类，如果为 True，则返回一个子类对象，否则返回一个与 a 数组具有相同数据类型和存储顺序的数组
shape	创建的数组的形状，如果不指定，则默认为 a 数组的形状。

例：

import numpy as np
 
# 创建一个 3x3 的二维数组
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
 
# 创建一个与 arr 形状相同的，所有元素都为 1 的数组
ones_arr = np.ones_like(arr)
print(ones_arr)

4.11 numpy.asarray

numpy.asarray 类似 numpy.array，但 numpy.asarray 参数只有三个，比 numpy.array 少两个。

numpy.asarray(a, dtype = None, order = None)

参数	描述
a	任意形式的输入参数，可以是，列表, 列表的元组, 元组, 元组的元组, 元组的列表，多维数组
dtype	数据类型，可选
order	可选，有"C"和"F"两个选项,分别代表，行优先和列优先，在计算机内存中的存储元素的顺序。

例：

import numpy as np 
 
x =  [1,2,3] 
a = np.asarray(x)  
print (a)

4.12 numpy.frombuffer

numpy.frombuffer 用于实现动态数组。

numpy.frombuffer 接受 buffer 输入参数，以流的形式读入转化成 ndarray 对象。

numpy.frombuffer(buffer, dtype = float, count = -1, offset = 0)

注意：buffer 是字符串的时候，Python3 默认 str 是 Unicode 类型，所以要转成 bytestring 在原 str 前加上 b。

参数	描述
buffer	可以是任意对象，会以流的形式读入。
dtype	返回数组的数据类型，可选
count	读取的数据数量，默认为-1，读取所有数据。
offset	读取的起始位置，默认为0。

例：

import numpy as np 
 
s =  b'Hello World' 
a = np.frombuffer(s, dtype =  'S1')  
print (a)

4.13 numpy.fromiter

numpy.fromiter 方法从可迭代对象中建立 ndarray 对象，返回一维数组。

numpy.fromiter(iterable, dtype, count=-1)

参数	描述
iterable	可迭代对象
dtype	返回数组的数据类型
count	读取的数据数量，默认为-1，读取所有数据

例：

import numpy as np 
 
# 使用 range 函数创建列表对象  
list=range(5)
it=iter(list)
 
# 使用迭代器创建 ndarray 
x=np.fromiter(it, dtype=float)
print(x)

4.14 numpy数组属性

NumPy 数组的维数称为秩（rank），秩就是轴的数量，即数组的维度，一维数组的秩为 1，二维数组的秩为 2，以此类推。

在 NumPy中，每一个线性的数组称为是一个轴（axis），也就是维度（dimensions）。比如说，二维数组相当于是两个一维数组，其中第一个一维数组中每个元素又是一个一维数组。所以一维数组就是 NumPy 中的轴（axis），第一个轴相当于是底层数组，第二个轴是底层数组里的数组。而轴的数量——秩，就是数组的维数。

很多时候可以声明 axis。axis=0，表示沿着第 0 轴进行操作，即对每一列进行操作；axis=1，表示沿着第1轴进行操作，即对每一行进行操作。

NumPy 的数组中比较重要 ndarray 对象属性有：

属性	说明
ndarray.ndim	秩，即轴的数量或维度的数量
ndarray.shape	数组的维度，对于矩阵，n 行 m 列
ndarray.size	数组元素的总个数，相当于 .shape 中 n*m 的值
ndarray.dtype	ndarray 对象的元素类型
ndarray.itemsize	ndarray 对象中每个元素的大小，以字节为单位
ndarray.flags	ndarray 对象的内存信息
ndarray.real	ndarray元素的实部
ndarray.imag	ndarray 元素的虚部
ndarray.data	包含实际数组元素的缓冲区，由于一般通过数组的索引获取元素，所以通常不需要使用这个属性。

使用reshape进行调整维度

numpy.reshape 函数可以在不改变数据的条件下修改形状，格式如下：

numpy.reshape(arr, newshape, order='C')

• arr：要修改形状的数组
• newshape：整数或者整数数组，新的形状应当兼容原有形状
• order：‘C’ – 按行，‘F’ – 按列，‘A’ – 原顺序，‘k’ – 元素在内存中的出现顺序。

例子：

a = np.arange(20)
a

a.reshape((4,5),order='F')

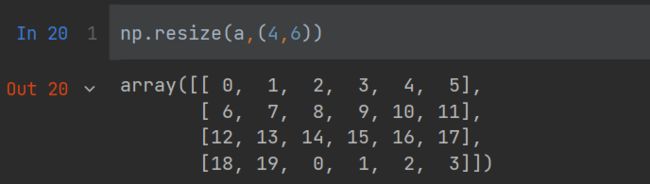
使用resize进行调整维度

numpy.resize 函数返回指定大小的新数组。

如果新数组大小大于原始大小，则包含原始数组中的元素的副本。

numpy.resize(arr, shape)

• arr：要修改大小的数组
• shape：返回数组的新形状

ndarray.resize(new_shape)，如果新数组大于原始数组用0而不是用重复的a进行填充

ndarray.resize(new_shape)

astype数据类型转换

numpy数据类型转换，调用astype返回数据类型修改后的数据，但是源数据的类型不会改变

a = np.array([1,1,1.2])
print('a的数据类型：',a.dtype)
print('astype修改数据类型：',a.astype('float32').dtype)
print('原数据类型未改变',a.dtype)

#正确操作
a = a.astype('float32')
print('修改类型后再次操作，类型改变：',a.dtype)

---

5. 切片和索引

ndarray对象的内容可以通过索引或切片来访问和修改，与 Python 中 list 的切片操作一样。

ndarray 数组可以基于 0 - n 的下标进行索引，切片对象可以通过内置的 slice 函数，并设置 start, stop 及 step 参数进行，从原数组中切割出一个新数组。

注意：区别在于数组切片是原始数组视图（这就意味着，如果做任何修改，原始都会跟着更改）。这也意味着，如果不想更改原始数组，我们需要进行显示的复制，从而得到它的副本（.copy()）。

5.1 一维数组操作

a = np.arange(10)
# 从索引2开始到索引7 间隔为2
b = a[2:7:2]
b

冒号:的解释：如果只放置一个参数，

• 如[2]，将返回该索引所对应的单个元素
• 如果为[2:]，表示从该索引开始以后的所有项都将被提取
• 如果使用了两个参数，如[2:7]，那么则提取两个索引（不包括停止索引）之间的项

# 取所有数据，步长为-1
a[::-1]

5.2 多维数组操作

注意：切片还可以使用省略号“…”，如果在行位置使用省略号，那么返回值将包含所有元素，反之，则包含所有列元素。

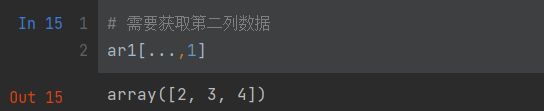
# 需要获取第二列数据
ar1[...,1]

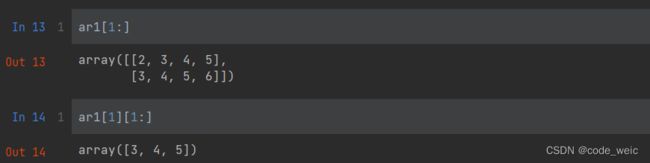
# 返回第二列后的所有项
ar1[...,1:]

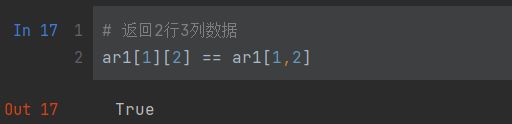
# 返回2行3列数据
ar1[1][2] == ar1[1,2]

# 需要获取第二行数据
ar1[1,...]

# 返回第二行后的所有项
ar1[1:,...]

...也可以使用:进行替换，效果相同，如

# 返回第二行后的所有项
ar1[1:,:]

5.3 整数数组索引

# 创建二维数组
x = np.array([
    [1,2],
    [3,4],
    [5,6]
])
# [0,1,2]代表行索引  [0,1,0]代表列索引
y = x[[0,1,2],[0,1,0]]
# y分别获取x中的(0,0)、(1,1)和(2,0)的数据
y

# 获取了4*3数组中的四个角上元素，它们对应的行索引是[0,0]和[3,3]，列索引是[0,2]和[0,2]
b = np.array([
    [0,1,2],
    [3,4,5],
    [6,7,8],
    [9,10,11] 
])
r = b[[0,0,3,3],[0,2,0,2]]
r

# 创建一个8×8的国际象棋棋盘矩阵（黑块为0，白块为1）
# [0 1 0 1 0 1 0 1]
# [1 0 1 0 1 0 1 0]
# [0 1 0 1 0 1 0 1]
# [1 0 1 0 1 0 1 0]
# [0 1 0 1 0 1 0 1]
# [1 0 1 0 1 0 1 0]
# [0 1 0 1 0 1 0 1]
# [1 0 1 0 1 0 1 0]

z = np.zeros((8,8),dtype=int)
z[1::2,::2] = 1
z[::2,1::2] = 1
z

5.4 布尔数组索引

当输出的结果需要经过布尔运算（如比较运算）时，此时会使用到另一种高级的索引方式，即布尔数组索引。

# 返回所有大于6的数字组成的数组
x = np.array([
    [0,1,2],
    [3,4,5],
    [6,7,8],
    [9,10,11]
])
x[x>6]

布尔索引实现的是通过一维数组中的每个元素的布尔型数值对一个与一维数组有着同样行数或列数的矩阵进行符合匹配。这种作用，其实是把一维数组中布尔值为True的相应行或列给抽取了出来。

注意：一维数组的长度必须和想要切片的维度或轴的长度一致。

练习：

• 提取出数组中所有奇数
• 将奇数值修改为-1

x[x%2!=0]
x[x%2!=0] = -1
x

筛选处指定区间内数据

&：和 |：或

x = np.array([
    [0,1,2],
    [3,4,5],
    [6,7,8],
    [9,10,11]
])
# 以上x中大于4并且小于9的数据
x[(x>4) & (x<9)]

x = np.array([
    [0,1,2],
    [3,4,5],
    [6,7,8],
    [9,10,11]
])
# 以上x中大于4或小于9的数据
x[(x>4) | (x<9)]

True和False的形式表示需要和不需要的数据

# 创建3*4的数组
a3_4 = np.arange(12).reshape(3,4)
# 行变量 存在3个元素
row1 = np.array([False,True,True])

# 列向量 存在4个元素
column1 = np.array([True,False,True,False])
a3_4[row1]
a3_4[:,column1]

总结：

>>>x = np.arange(10)
>>>x
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]))

# 简单索引
>>>x[3]
3

# 一维切片
>>>x = np.arange(10)
>>>x[1:7:2]
array([1, 3, 5])

# 多维切片
>>>y = np.arange(20).reshape(4,5)
>>>y
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])

>>>y[1:4, 1:4]
array([[ 6,  7,  8],
       [11, 12, 13],
       [16, 17, 18]])

# i和j为负，则可看作为n+i和n+j，n为维度中元素数量。
# k为负，则步长向前。
>>>x[-2:10]
array([8, 9])

>>>x[-3:3:-1]
array([7, 6, 5, 4])

# 默认写法 ":"
>>>x[4:]
array([4, 5, 6, 7, 8, 9])

# 如果索引元组的元素数小于维度，则假定任何其它维
>>> z = np.array([[[1],[2],[3]], [[4],[5],[6]]])
>>> z.shape
(2, 3, 1)
>>> z[1:2]
array([[[4],
        [5]
        [6]]])

# 索引中可以使用 "..." 代指其它维度的全部索引，一个索引中只能有一个省略号
>>>z[...,0]
array([[1, 2, 3],
        [4, 5, 6]])

# 使用newaxis 增加维度
>>>z[:,np.newaxis,:,:].shape
(2, 1, 3, 1)

# --------------------------------------------------------------------------------

# 整数数组分别表示所需索引的下标。
# 取点[0,0], [1,1], [2,0]
>>>x = np.array([[1,  2],  [3,  4],  [5,  6]]) 
>>>x[[0,1,2],  [0,1,0]]  
array([1, 4, 5])

# 获取了 4X3 数组中的四个角的元素。 
# 行索引是 [0,0] 和 [3,3]，而列索引是 [0,2] 和 [0,2]。

>>> x = array([[ 0,  1,  2],
               [ 3,  4,  5],
               [ 6,  7,  8],
               [ 9, 10, 11]])
>>> rows = np.array([[0, 0],
...                  [3, 3]], dtype=np.intp)
>>> columns = np.array([[0, 2],
...                     [0, 2]], dtype=np.intp)
>>> x[rows, columns]
array([[ 0,  2],
       [ 9, 11]])
# 使用np.ix_(rows, columns)获得相同效果
>>>x[[0,3], [0,2]

     
----------------------------------------------------------------------
     
# 对于array[obj]
# 如果array.ndim == obj.ndim，
# 将返回一个一维数组，其中包含所有obj中为 True 的位置的元素，以row-major为顺序。
>>>x = np.array([[1., 2.], [np.nan, 3.], [np.nan, np.nan]])
>>>np.isnan(x),x[~np.isnan(x)]
(array([[False, False],
        [ True, False],
        [ True,  True]]),
 array([1., 2., 3.]))

# 使用ix_()功能
>>> x = array([[ 0,  1,  2],
               [ 3,  4,  5],
               [ 6,  7,  8],
               [ 9, 10, 11]])
>>> rows = (x.sum(-1) % 2) == 0
>>> rows
array([False,  True, False,  True])
>>> columns = [0, 2]
>>> x[np.ix_(rows, columns)]
array([[ 3,  5],
       [ 9, 11]])

---

6. numpy广播机制

广播(Broadcast)是 numpy 对不同形状(shape)的数组进行数值计算的方式， 对数组的算术运算通常在相应的元素上进行。

如果两个数组 a 和 b 形状相同，即满足 a.shape == b.shape，那么 a*b 的结果就是 a 与 b 数组对应位相乘。这要求维数相同，且各维度的长度相同。

a = np.array([10,20,30,40])
b = np.array([1,2,3,4])
c = a * b
print(c)
# [ 10  40  90 160]

但是如果两个形状不同的数组呢？它们之间就不能做算术运算了吗？当然不是！为了保证数组形状相同，Numpy设计了一种广播机制，这种机制的核心是对形状较小的数组，在横向或纵向上进行一定次数的重复，使其与较大的数组拥有相同的维度。

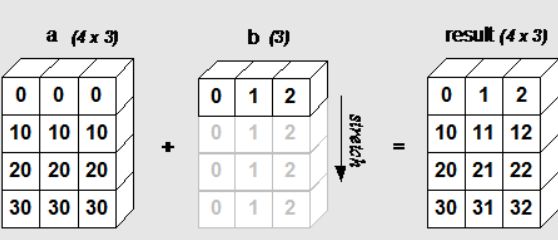
下面的图片展示了数组 b 如何通过广播来与数组 a 兼容。

4x3 的二维数组与长为 3 的一维数组相加，等效于把数组 b 在二维上重复 4 次再运算：

a = np.array([[ 0, 0, 0],
           [10,10,10],
           [20,20,20],
           [30,30,30]])
b = np.array([1,2,3])
bb = np.tile(b, (4, 1))  # 重复 b 的各个维度
print(a + bb)
'''[[ 1  2  3]
 [11 12 13]
 [21 22 23]
 [31 32 33]]'''

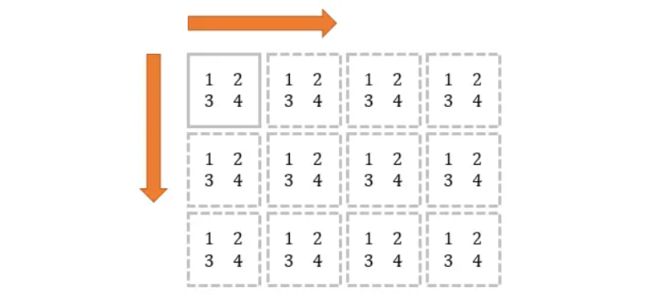
Numpy的 tile() 函数，就是将原矩阵横向、纵向地复制。

举个例子，原矩阵：

mat = array([[1,2], [3, 4]])

横向：

tile(mat, (1, 4))
# 等同于
tile(mat, 4)

# 结果为：
[[1 2 1 2 1 2 1 2]
 [3 4 3 4 3 4 3 4]]

纵向：

tile(mat, (3, 1))
#结果为：
[[1 2]
 [3 4]
 [1 2]
 [3 4]
 [1 2]
 [3 4]]

横向+纵向：

tile(mat, (3, 4))
# 结果为：
[[1 2 1 2 1 2 1 2]
 [3 4 3 4 3 4 3 4]
 [1 2 1 2 1 2 1 2]
 [3 4 3 4 3 4 3 4]
 [1 2 1 2 1 2 1 2]
 [3 4 3 4 3 4 3 4]]

广播的规则:

• 让所有输入数组都向其中形状最长的数组看齐，形状中不足的部分都通过在前面加 1 补齐。
• 输出数组的形状是输入数组形状的各个维度上的最大值。
• 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时，这个数组能够用来计算，否则出错。
• 当输入数组的某个维度的长度为 1 时，沿着此维度运算时都用此维度上的第一组值。

**简单理解：**对两个数组，分别比较他们的每一个维度（若其中一个数组没有当前维度则忽略），满足：

• 数组拥有相同形状。
• 当前维度的值相等。
• 当前维度的值有一个是 1。

另一种对广播规则的简单理解：

• 将两个数组的维度大小右对齐，然后比较对应维度上的数值，如果数值相等或者其中有一个为1或者为空，则能进行广播运算。
• 输出的维度大小为取数值大的数值，否则不能进行数组运算。

例如：

数组a大小为(2,3)
数组b大小为(1,)

首先右对齐：

​ 2 3

​ 1

–------------------------------------------------

​ 2 3

所以最后两个数组运算的输出大小为：(2,3)

---

7. numpy统计

NumPy 提供了很多统计函数，用于从数组中查找最小元素，最大元素，百分位标准差和方差等。

7.1 平均值和中位数

平均值

numpy.mean() 函数返回数组中元素的算术平均值。 如果提供了轴，则沿其计算。

算术平均值是沿轴的元素的总和除以元素的数量。

m1 = np.arange(20).reshape((4,5))
m1.mean()

# 9.5

若想求某一维度的平均值，设置axis参数，多维数组的元素指定

• axis = 0，将从上往下计算
• axis = 1，将从左往右计算

m1.mean(axis=0)
m1.mean(axis=1)
# array([ 7.5,  8.5,  9.5, 10.5, 11.5])
# array([ 2.,  7., 12., 17.])

中位数

numpy.median() 函数用于计算数组 a 中元素的中位数（中值）

是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值

• 平均数:是一个"虚拟"的数，是通过计算得到的，它不是数据中的原始数据。中位数:是一个不完全"虚拟"的数。
• 平均数:反映了一组数据的平均大小，常用来一代表数据的总体"平均水平"。中位数:像一条分界线，将数据分成前半部分和后半部分，因此用来代表一组数据的"中等水平"。

同样，也可以设置axis的值

• axis = 0，将从上往下计算
• axis = 1，将从左往右计算

'''
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])
'''

np.median(m1)
np.median(m1,axis=0)
np.median(m1,axis=1)

# 9.5
# array([ 7.5,  8.5,  9.5, 10.5, 11.5])
# array([ 2.,  7., 12., 17.])

7.2 标准差和方差

标准差

标准差是一组数据平均值分散程度的一种度量，在概率统计中最常使用作为统计分布程度上的测量,是反映一组数据离散程度最常用的一种量化形式。

标准差是方差的算术平方根。

简单来说，标准差是一组数据平均值分散程度的一种度量。

• 一个较大的标准差，代表大部分数值和其平均值之间差异较大
• 一个较小的标准差，代表这些数值较接近平均值

std = sqrt(mean((x - x.mean())**2))

a = np.array([95,85,75,65,55,45])
b = np.array([73,72,71,69,68,67])
# 计算标准差
print(np.std(a))
print(np.std(b))

# 17.07825127659933
# 2.160246899469287

import math
# 按步骤计算下标准差
math.sqrt(sum((a - np.mean(a))**2)/a.size)
# 17.07825127659933

方差

统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数，即 $\ mean((x - x.mean())** 2) \ $

换句话说，标准差是方差的平方根。方差是衡量随机变量或一组数据时离散程度的度量。

import numpy as np
 
print (np.var([1,2,3,4]))
# 1.25

标准差有计量单位，而方差无计量单位，但两者的作用一样，虽然能很好的描述数据与均值的偏离程度，但是处理结果是不符合我们的直观思维的。

7.3 最大最小与求和

最大与最小

numpy.amin() 用于计算数组中的元素沿指定轴的最小值。

numpy.amax() 用于计算数组中的元素沿指定轴的最大值。

x = np.array([1,2,3,4,5,6,8,0,11,37,23,12]).reshape((3,4))
x
'''
array([[ 1,  2,  3,  4],
       [ 5,  6,  8,  0],
       [11, 37, 23, 12]])
'''

# 最大值
print(x.max())
# 最小值
print(x.min())
# 在X轴上的最大值
print(x.max(axis=1))
# 在Y轴上的最小值
print(x.min(axis=0))
'''
37
0
[ 4  8 37]
[1 2 3 0]
'''

求和

ndarray.sum()

x = np.array([
    [1,2,3,4],
    [5,6,7,8],
    [10,11,12,13]
])
print(x.sum())
print(x.sum(axis=1))
print(x.sum(axis=0))
# 82
# [10 26 46]
# [16 19 22 25]

7.4 加权平均数

numpy.average() 函数根据在另一个数组中给出的各自的权重计算数组中元素的加权平均值。

该函数可以接受一个轴参数。 如果没有指定轴，则数组会被展开。

加权平均值即将各数值乘以相应的权数，然后加总求和得到总体值，再除以总的单位数。

考虑数组[1,2,3,4]和相应的权重[4,3,2,1]，通过将相应元素的乘积相加，并将和除以权重的和，来计算加权平均值。

numpy.average(a,axis=None,weights=None,returned=False)

• weights:数组，可选

• 与a中的值关联的权重数组。a中的每个值都根据其关联的权重对平均值做出贡献。权重数组可以是一维的(在这种情况下，它的长度必须是沿给定轴的a的大小)或与a具有相同的形状。如果weights=None，则假定a 中的所有数据的权重等于1。一维计算是:

  $\ avg=sum(a*weights)/sum(weights) \ $

  对权重的唯一限制是sum(weights)不能为0。

x = np.array([
    [1,2,3,4],
    [5,6,7,8],
    [10,11,12,13]
])
w = np.array([
    [1,2,3,4],
    [5,6,7,8],
    [10,11,12,13]
])
print(np.average(x))
print(np.average(x,weights=w))
# 6.833333333333333
# 9.0

xiaoming = np.array([80,90,85])
xiaogang = np.array([85,90,80])
weights = np.array([0.2,0.3,0.5])
xiaoming_z = np.average(xiaoming,weights=weights)
xiaogang_z = np.average(xiaogang,weights=weights)
print(xiaoming_z)
print(xiaogang_z)
if xiaogang_z>xiaoming_z:
    print("小刚")
else:
    print("小明")

# 85.5
# 84.0
# 小明

---

8. 数组操作

8.1 修改数组形状

函数	描述
reshape	不改变数据的条件下修改形状
flat	数组元素迭代器
flatten	返回一份数组拷贝，对拷贝所做的修改不会影响原始数组
ravel	返回展开数组

numpy.reshape

numpy.reshape 函数可以在不改变数据的条件下修改形状，格式如下：

numpy.reshape(arr, newshape, order='C')

• arr：要修改形状的数组
• newshape：整数或者整数数组，新的形状应当兼容原有形状
• order：‘C’ – 按行，‘F’ – 按列，‘A’ – 原顺序，‘k’ – 元素在内存中的出现顺序。

numpy.ndarray.flat

numpy.ndarray.flat 是一个数组元素迭代器，如

a = np.arange(9).reshape(3,3) 
 
#对数组中每个元素都进行处理，可以使用flat属性，该属性是一个数组元素迭代器：
print ('迭代后的数组：')
for element in a.flat:
    print (element)

numpy.ndarray.flatten

numpy.ndarray.flatten 返回一份数组拷贝，对拷贝所做的修改不会影响原始数组，格式如下：

ndarray.flatten(order='C')

参数说明：

• order：‘C’ – 按行，‘F’ – 按列，‘A’ – 原顺序，‘K’ – 元素在内存中的出现顺序。

numpy.ravel

numpy.ravel() 展平的数组元素，顺序通常是"C风格"，返回的是数组视图（view，有点类似 C/C++引用reference的意味），修改会影响原始数组。

该函数接收两个参数：

numpy.ravel(a, order='C')

参数说明：

• order：‘C’ – 按行，‘F’ – 按列，‘A’ – 原顺序，‘K’ – 元素在内存中的出现顺序。

8.2 翻转数组

函数	描述
transpose	对换数组的维度
ndarray.T	和 self.transpose() 相同
rollaxis	向后滚动指定的轴
swapaxes	对换数组的两个轴

numpy.transpose

numpy.transpose 函数用于对换数组的维度，格式如下：

numpy.transpose(arr, axes)

参数说明:

• arr：要操作的数组
• axes：整数列表，对应维度，通常所有维度都会对换。

numpy.rollaxis

numpy.rollaxis 函数向后滚动特定的轴到一个特定位置，格式如下：

numpy.rollaxis(arr, axis, start)

参数说明：

• arr：数组
• axis：要向后滚动的轴，其它轴的相对位置不会改变
• start：默认为零，表示完整的滚动。会滚动到特定位置。

numpy.swapaxes

numpy.swapaxes 函数用于交换数组的两个轴，格式如下：

numpy.swapaxes(arr, axis1, axis2)

• arr：输入的数组
• axis1：对应第一个轴的整数
• axis2：对应第二个轴的整数

8.3 修改数组维度

维度	描述
broadcast	产生模仿广播的对象
broadcast_to	将数组广播到新形状
expand_dims	扩展数组的形状
squeeze	从数组的形状中删除一维条目

numpy.broadcast

numpy.broadcast 用于模仿广播的对象，它返回一个对象，该对象封装了将一个数组广播到另一个数组的结果。

该函数使用两个数组作为输入参数.

numpy.broadcast_to

numpy.broadcast_to 函数将数组广播到新形状。它在原始数组上返回只读视图。 它通常不连续。 如果新形状不符合 NumPy 的广播规则，该函数可能会抛出ValueError。

numpy.broadcast_to(array, shape, subok)

numpy.expand_dims

numpy.expand_dims 函数通过在指定位置插入新的轴来扩展数组形状，函数格式如下:

 numpy.expand_dims(arr, axis)

参数说明：

• arr：输入数组
• axis：新轴插入的位置

numpy.squeeze

numpy.squeeze 函数从给定数组的形状中删除一维的条目，函数格式如下：

numpy.squeeze(arr, axis)

参数说明：

• arr：输入数组
• axis：整数或整数元组，用于选择形状中一维条目的子集

8.4 连接数组

函数	描述
concatenate	连接沿现有轴的数组序列
stack	沿着新的轴加入一系列数组。
hstack	水平堆叠序列中的数组（列方向）
vstack	竖直堆叠序列中的数组（行方向）

numpy.concatenate

numpy.concatenate 函数用于沿指定轴连接相同形状的两个或多个数组，格式如下：

numpy.concatenate((a1, a2, ...), axis)

参数说明：

• a1, a2, ...：相同类型的数组
• axis：沿着它连接数组的轴，默认为 0

numpy.stack

numpy.stack 函数用于沿新轴连接数组序列，格式如下：

numpy.stack(arrays, axis)

参数说明：

• arrays相同形状的数组序列
• axis：返回数组中的轴，输入数组沿着它来堆叠

numpy.hstack

numpy.hstack 是 numpy.stack 函数的变体，它通过水平堆叠来生成数组。

numpy.vstack

numpy.vstack 是 numpy.stack 函数的变体，它通过垂直堆叠来生成数组。

8.5 分割数组

函数	数组及操作
split	将一个数组分割为多个子数组
hsplit	将一个数组水平分割为多个子数组（按列）
vsplit	将一个数组垂直分割为多个子数组（按行）

numpy.split

numpy.split 函数沿特定的轴将数组分割为子数组，格式如下：

numpy.split(ary, indices_or_sections, axis)

参数说明：

• ary：被分割的数组
• indices_or_sections：如果是一个整数，就用该数平均切分，如果是一个数组，为沿轴切分的位置（左开右闭）
• axis：设置沿着哪个方向进行切分，默认为 0，横向切分，即水平方向。为 1 时，纵向切分，即竖直方向。

numpy.hsplit

numpy.hsplit 函数用于水平分割数组，通过指定要返回的相同形状的数组数量来拆分原数组。

numpy.vsplit

numpy.vsplit 沿着垂直轴分割，其分割方式与hsplit用法相同。

8.6 数组元素的添加与删除

函数	元素及描述
resize	返回指定形状的新数组
append	将值添加到数组末尾
insert	沿指定轴将值插入到指定下标之前
delete	删掉某个轴的子数组，并返回删除后的新数组
unique	查找数组内的唯一元素

numpy.resize

numpy.resize 函数返回指定大小的新数组。

如果新数组大小大于原始大小，则包含原始数组中的元素的副本。

numpy.resize(arr, shape)

参数说明：

• arr：要修改大小的数组
• shape：返回数组的新形状

numpy.append

numpy.append 函数在数组的末尾添加值。 追加操作会分配整个数组，并把原来的数组复制到新数组中。 此外，输入数组的维度必须匹配否则将生成ValueError。

append 函数返回的始终是一个一维数组。

numpy.append(arr, values, axis=None)

参数说明：

• arr：输入数组
• values：要向arr添加的值，需要和arr形状相同（除了要添加的轴）
• axis：默认为 None。当axis无定义时，是横向加成，返回总是为一维数组！当axis有定义的时候，分别为0和1的时候。当axis有定义的时候，分别为0和1的时候（列数要相同）。当axis为1时，数组是加在右边（行数要相同）。

numpy.insert

numpy.insert 函数在给定索引之前，沿给定轴在输入数组中插入值。

如果值的类型转换为要插入，则它与输入数组不同。 插入没有原地的，函数会返回一个新数组。 此外，如果未提供轴，则输入数组会被展开。

numpy.insert(arr, obj, values, axis)

参数说明：

• arr：输入数组
• obj：在其之前插入值的索引
• values：要插入的值
• axis：沿着它插入的轴，如果未提供，则输入数组会被展开

numpy.delete

numpy.delete 函数返回从输入数组中删除指定子数组的新数组。 与 insert() 函数的情况一样，如果未提供轴参数，则输入数组将展开。

Numpy.delete(arr, obj, axis)

参数说明：

• arr：输入数组
• obj：可以被切片，整数或者整数数组，表明要从输入数组删除的子数组
• axis：沿着它删除给定子数组的轴，如果未提供，则输入数组会被展开

numpy.unique

numpy.unique 函数用于去除数组中的重复元素。

numpy.unique(arr, return_index, return_inverse, return_counts)

• arr：输入数组，如果不是一维数组则会展开
• return_index：如果为true，返回新列表元素在旧列表中的位置（下标），并以列表形式储
• return_inverse：如果为true，返回旧列表元素在新列表中的位置（下标），并以列表形式储
• return_counts：如果为true，返回去重数组中的元素在原数组中的出现次数

9. numpy数据类型

numpy 支持的数据类型比 Python 内置的类型要多很多，基本上可以和 C 语言的数据类型对应上，其中部分类型对应为 Python 内置的类型。下表列举了常用 NumPy 基本类型。

名称	描述
bool_	布尔型数据类型（True 或者 False）
int_	默认的整数类型（类似于 C 语言中的 long，int32 或 int64）
intc	与 C 的 int 类型一样，一般是 int32 或 int 64
intp	用于索引的整数类型（类似于 C 的 ssize_t，一般情况下仍然是 int32 或 int64）
int8	字节（-128 to 127）
int16	整数（-32768 to 32767）
int32	整数（-2147483648 to 2147483647）
int64	整数（-9223372036854775808 to 9223372036854775807）
uint8	无符号整数（0 to 255）
uint16	无符号整数（0 to 65535）
uint32	无符号整数（0 to 4294967295）
uint64	无符号整数（0 to 18446744073709551615）
float_	float64 类型的简写
float16	半精度浮点数，包括：1 个符号位，5 个指数位，10 个尾数位
float32	单精度浮点数，包括：1 个符号位，8 个指数位，23 个尾数位
float64	双精度浮点数，包括：1 个符号位，11 个指数位，52 个尾数位
complex_	complex128 类型的简写，即 128 位复数
complex64	复数，表示双 32 位浮点数（实数部分和虚数部分）
complex128	复数，表示双 64 位浮点数（实数部分和虚数部分）

numpy 的数值类型实际上是 dtype 对象的实例，并对应唯一的字符，包括 np.bool_，np.int32，np.float32，等等。

数据类型对象 (dtype)

数据类型对象（numpy.dtype 类的实例）用来描述与数组对应的内存区域是如何使用，它描述了数据的以下几个方面：：

• 数据的类型（整数，浮点数或者 Python 对象）
• 数据的大小（例如， 整数使用多少个字节存储）
• 数据的字节顺序（小端法或大端法）
• 在结构化类型的情况下，字段的名称、每个字段的数据类型和每个字段所取的内存块的部分
• 如果数据类型是子数组，那么它的形状和数据类型是什么。

字节顺序是通过对数据类型预先设定 < 或 > 来决定的。 < 意味着小端法(最小值存储在最小的地址，即低位组放在最前面)。> 意味着大端法(最重要的字节存储在最小的地址，即高位组放在最前面)。

dtype 对象是使用以下语法构造的：

numpy.dtype(object, align, copy)

• object - 要转换为的数据类型对象
• align - 如果为 true，填充字段使其类似 C 的结构体。
• copy - 复制 dtype 对象 ，如果为 false，则是对内置数据类型对象的引用

每个内建类型都有一个唯一定义它的字符代码，如下：

字符	对应类型
b	布尔型
i	(有符号) 整型
u	无符号整型 integer
f	浮点型
c	复数浮点型
m	timedelta（时间间隔）
M	datetime（日期时间）
O	(Python) 对象
S, a	(byte-)字符串
U	Unicode
V	原始数据 (void)

---

11. numpy文件操作

Numpy 可以读写磁盘上的文本数据或二进制数据。

NumPy 为 ndarray 对象引入了一个简单的文件格式：npy。

npy 文件用于存储重建 ndarray 所需的数据、图形、dtype 和其他信息。

常用的 IO 函数有：

• load() 和 save() 函数是读写文件数组数据的两个主要函数，默认情况下，数组是以未压缩的原始二进制格式保存在扩展名为 .npy 的文件中。
• savez() 函数用于将多个数组写入文件，默认情况下，数组是以未压缩的原始二进制格式保存在扩展名为 .npz 的文件中。
• loadtxt() 和 savetxt() 函数处理正常的文本文件(.txt 等)

loadtxt读取txt文本、Csv文件

loadtxt(fname,dtype=<type 'float'>，comments='#',delimiter=None，converters=None，skiprows=0，usecols=None,unpack=False,ndmin=0, encoding='bytes')

参数:

• fname:指定文件名称或字符串。支持压缩文件，包括gz、bz格式。
• dtype:数据类型。默认float。
• comments:字符串或字符串组成的列表。表示注释字符集开始的标志，默认为#。
• dellmiter:字符串。分隔符。
• converters:字典。将特定列的数据转换为字典中对应的函数的浮点型数据。例如将空值转换为0，默认为空。
• skiprows:跳过特定行数据。例如跳过前1行（可能是标题或注释)。默认为0。
• usecols:元组。用来指定要读取数据的列，第一列为0。例如(1，3，5)，默认为空。
• unpack:布尔型。指定是否转置数组，如果为真则转置，默认为False。
• ndmin:整数型。指定返回的数组至少包含特定维度的数组。值域为0、1、2，默认为0。
• encoding:编码,确认文件是gbk还是utf-8格式

例：

# 不读取以#开头的注释  默认为浮点类型
data = np.loadtxt("test.txt")
print(data)
print(data.shape)
'''
[[ 0.  1.  2.  3.  4.  5.  6.  7.  8.  9.]
 [10. 11. 12. 13. 14. 15. 16. 17. 18. 19.]
 [30. 31. 32. 33. 34. 35. 36. 37. 38. 39.]]
(3, 10)
'''

# 读取为整型
np.loadtxt("test.txt",dtype="int32")
'''
array([[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
       [30, 31, 32, 33, 34, 35, 36, 37, 38, 39]])
'''

# 数据由不同列数据标识的含义和类型不同，因此需要自定义数据类型
user_info = np.dtype([('name','U10'),('age','i1'),('gender','U1'),('height','i2')])
# 使用自定义的数据类型 读取数据
student = np.loadtxt("test.csv",delimiter=",",skiprows=1,encoding="utf8",dtype=user_info)

numpy.save()

numpy.save() 函数将数组保存到以 .npy 为扩展名的文件中。

numpy.save(file, arr, allow_pickle=True, fix_imports=True)

参数说明：

• file：要保存的文件，扩展名为 .npy，如果文件路径末尾没有扩展名 .npy，该扩展名会被自动加上。
• arr: 要保存的数组
• allow_pickle: 可选，布尔值，允许使用 Python pickles 保存对象数组，Python 中的 pickle 用于在保存到磁盘文件或从磁盘文件读取之前，对对象进行序列化和反序列化。
• fix_imports: 可选，为了方便 Pyhton2 中读取 Python3 保存的数据。

np.savez

numpy.savez() 函数将多个数组保存到以 npz 为扩展名的文件中。

numpy.savez(file, *args, **kwds)

参数说明：

• file：要保存的文件，扩展名为 .npz，如果文件路径末尾没有扩展名 .npz，该扩展名会被自动加上。
• args: 要保存的数组，可以使用关键字参数为数组起一个名字，非关键字参数传递的数组会自动起名为 arr_0, arr_1, …　。
• kwds: 要保存的数组使用关键字名称。

savetxt()

savetxt() 函数是以简单的文本文件格式存储数据，对应的使用 loadtxt() 函数来获取数据。

np.loadtxt(FILENAME, dtype=int, delimiter=' ')
np.savetxt(FILENAME, a, fmt="%d", delimiter=",")

参数 delimiter 可以指定各种分隔符、针对特定列的转换器函数、需要跳过的行数等。

---

12. numpy随机数

numpy.random.rand(d0,d1,…dn)

• rand函数根据给定维度生成[0,1)之间的数据，包含0，不包含1

• dn表示每个维度

• 返回值为指定维度的array

# 创建4行2列的随机数据
np.random.rand(4,2)

'''
array([[0.35351577, 0.08201327],
       [0.90198115, 0.95222547],
       [0.31488553, 0.76634463],
       [0.61681158, 0.82021047]])
'''

# 创建2块2行3列的随机数据
np.random.rand(2,2,3)
'''
array([[[0.10668341, 0.36414521, 0.41893531],
        [0.45225353, 0.37678331, 0.52941225]],

       [[0.89474814, 0.4959978 , 0.18457943],
        [0.93247073, 0.7842147 , 0.69360269]]])
'''

numpy.random.randn(d0,d1,…,dn)

• randn函数返回一个或一组样本，具有标准正态分布

• dn表示每个维度

• 返回值为指定维度的array

标准正态分布又称为u分布，是以O为均值、以1为标准差的正态分布，记为N(0，1)。

numpy.random.randint()

numpy.random.randint(low,high=None,size=None，dtype=’1’)

• 返回随机整数，范围区间为[low,high) ，包含low，不包含high
• 参数: low为最小值，high为最大值，size为数组维度大小，dtype为数据类型，默认的数据类型是np.int
• high没有填写时，默认生成随机数的范围是[0，low)

# 返回[1,0)之间的整数，所以只有0
np.random.randint(2,size=5)
# array([0, 0, 0, 1, 0])

# 返回一个[1,5)之间的随机整数
np.random.randint(1,5)
# 1

# 返回 -5到5之间不包含5的 2行2列数据
np.random.randint(-5,5,size=(2,2))
'''
array([[-3, -4],
       [ 0,  1]])
'''

# 返回 -5到5之间不包含5的 2行2列数据
np.random.randint(-5,5,size=(2,2,2))
'''
array([[[ 3,  4],
        [-3, -1]],

       [[-3,  4],
        [ 3,  2]]])
'''

numpy.random.sample

numpy.random.sample(size=None)

返回半开区间内的随机浮点数[0.0,1.0]

np.random.sample((2,3))
'''
array([[0.1065663 , 0.39375493, 0.20151713],
       [0.37460542, 0.05495299, 0.20242287]])
'''

随机种子 np.random.seed()

使用相同的seed()值，则每次生成的随机数都相同,使得随机数可以预测

但是，只在调用的时候seed()一下并不能使生成的随机数相同，需要每次调用都seed()一下，表示种子相同，从而生成的随机数相同。

np.random.seed(1)
print(np.random.randn(3,3))
print("="*10)
np.random.seed(1)
print(np.random.randn(3,3))

'''
[[ 1.62434536 -0.61175641 -0.52817175]
 [-1.07296862  0.86540763 -2.3015387 ]
 [ 1.74481176 -0.7612069   0.3190391 ]]
==========
[[ 1.62434536 -0.61175641 -0.52817175]
 [-1.07296862  0.86540763 -2.3015387 ]
 [ 1.74481176 -0.7612069   0.3190391 ]]
'''

正态分布 numpy.random.normal

numpy.random.normal(loc=0.0,scale=1.0,size=None)

作用:返回一个由size指定形状的数组，数组中的值服从u=loc,o=scale的正态分布。

参数:

• loc : float型或者float型的类数组对象，指定均值$\ \mu \ $
• scale : float型或者float型的类数组对象，指定标准差$\ \sigma \ $
• size : int型或者int型的元组，指定了数组的形状。如果不提供size，且loc和scale为标量(不是类数组对象)，则返回一个服从该分布的随机数。

# 标准正态分布，3行2列
np.random.normal(0,1,(3,2))
'''
array([[-0.24937038,  1.46210794],
       [-2.06014071, -0.3224172 ],
       [-0.38405435,  1.13376944]])
'''

# 均值为1，标准差为3
np.random.normal(1,3,(3,2))
'''
array([[-2.2996738 ,  0.48271538],
       [-1.63357525,  1.12664124],
       [ 2.74844564, -2.30185753]])
'''

---

13. numpy函数

13.1 字符串函数

函数	描述
add()	对两个数组的逐个字符串元素进行连接
multiply()	返回按元素多重连接后的字符串
center()	居中字符串
capitalize()	将字符串第一个字母转换为大写
title()	将字符串的每个单词的第一个字母转换为大写
lower()	数组元素转换为小写
upper()	数组元素转换为大写
split()	指定分隔符对字符串进行分割，并返回数组列表
splitlines()	返回元素中的行列表，以换行符分割
strip()	移除元素开头或者结尾处的特定字符
join()	通过指定分隔符来连接数组中的元素
replace()	使用新字符串替换字符串中的所有子字符串
decode()	数组元素依次调用str.decode
encode()	数组元素依次调用str.encode

13.2 NumPy 数学函数

三角函数

NumPy 提供了标准的三角函数：sin()、cos()、tan()。

arcsin，arccos，和 arctan 函数返回给定角度的 sin，cos 和 tan 的反三角函数。

这些函数的结果可以通过 numpy.degrees() 函数将弧度转换为角度。

舍入函数

numpy.around() 函数返回指定数字的四舍五入值。

numpy.around(a,decimals)

参数说明：

• a: 数组
• decimals: 舍入的小数位数。 默认值为0。 如果为负，整数将四舍五入到小数点左侧的位置

numpy.floor()

numpy.floor() 返回小于或者等于指定表达式的最大整数，即向下取整。

numpy.ceil()

numpy.ceil() 返回大于或者等于指定表达式的最小整数，即向上取整。

13.3 NumPy 算术函数

NumPy 算术函数包含简单的加减乘除: add()，subtract()，multiply() 和 divide()。

需要注意的是数组必须具有相同的形状或符合数组广播规则。

numpy.reciprocal()

numpy.reciprocal() 函数返回参数逐元素的倒数。如 1/4 倒数为 4/1。

numpy.power()

numpy.power() 函数将第一个输入数组中的元素作为底数，计算它与第二个输入数组中相应元素的幂。

numpy.mod()

numpy.mod() 计算输入数组中相应元素的相除后的余数。 函数 numpy.remainder() 也产生相同的结果。

13.4 NumPy 排序、条件筛选函数

NumPy 提供了多种排序的方法。 这些排序函数实现不同的排序算法，每个排序算法的特征在于执行速度，最坏情况性能，所需的工作空间和算法的稳定性。 下表显示了三种排序算法的比较。

种类	速度	最坏情况	工作空间	稳定性
'quicksort'（快速排序）	1	O(n^2)	0	否
'mergesort'（归并排序）	2	O(n*log(n))	~n/2	是
'heapsort'（堆排序）	3	O(n*log(n))	0	否

numpy.sort()

numpy.sort() 函数返回输入数组的排序副本。函数格式如下：

numpy.sort(a, axis, kind, order)

参数说明：

• a: 要排序的数组
• axis: 沿着它排序数组的轴，如果没有数组会被展开，沿着最后的轴排序， axis=0 按列排序，axis=1 按行排序
• kind: 默认为’quicksort’（快速排序）
• order: 如果数组包含字段，则是要排序的字段

numpy.argsort()

numpy.argsort() 函数返回的是数组值从小到大的索引值。

numpy.lexsort()

numpy.lexsort() 用于对多个序列进行排序。把它想象成对电子表格进行排序，每一列代表一个序列，排序时优先照顾靠后的列。

这里举一个应用场景：小升初考试，重点班录取学生按照总成绩录取。在总成绩相同时，数学成绩高的优先录取，在总成绩和数学成绩都相同时，按照英语成绩录取…… 这里，总成绩排在电子表格的最后一列，数学成绩在倒数第二列，英语成绩在倒数第三列。

msort、sort_complex、partition、argpartition

函数	描述
msort(a)	数组按第一个轴排序，返回排序后的数组副本。np.msort(a) 相等于 np.sort(a, axis=0)。
sort_complex(a)	对复数按照先实部后虚部的顺序进行排序。
partition(a, kth[, axis, kind, order])	指定一个数，对数组进行分区
argpartition(a, kth[, axis, kind, order])	可以通过关键字 kind 指定算法沿着指定轴对数组进行分区

numpy.argmax() 和 numpy.argmin()

numpy.argmax() 和 numpy.argmin()函数分别沿给定轴返回最大和最小元素的索引。

numpy.nonzero()

numpy.nonzero() 函数返回输入数组中非零元素的索引。

numpy.where()

numpy.where() 函数返回输入数组中满足给定条件的元素的索引。

numpy.extract()

numpy.extract() 函数根据某个条件从数组中抽取元素，返回满条件的元素。

---

14. 线性代数

NumPy 提供了线性代数函数库 linalg，该库包含了线性代数所需的所有功能，可以看看下面的说明：

函数	描述
dot	两个数组的点积，即元素对应相乘。
vdot	两个向量的点积
inner	两个数组的内积
matmul	两个数组的矩阵积
determinant	数组的行列式
solve	求解线性矩阵方程
inv	计算矩阵的乘法逆矩阵

14.1 numpy.dot()

numpy.dot() 对于两个一维的数组，计算的是这两个数组对应下标元素的乘积和(数学上称之为向量点积)；对于二维数组，计算的是两个数组的矩阵乘积；对于多维数组，它的通用计算公式如下，即结果数组中的每个元素都是：数组a的最后一维上的所有元素与数组b的倒数第二位上的所有元素的乘积和： dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])。

numpy.dot(a, b, out=None) 

参数说明：

• a : ndarray 数组
• b : ndarray 数组
• out : ndarray, 可选，用来保存dot()的计算结果

14.2 numpy.vdot()

numpy.vdot() 函数是两个向量的点积。 如果第一个参数是复数，那么它的共轭复数会用于计算。 如果参数是多维数组，它会被展开。

14.3 numpy.inner()

numpy.inner() 函数返回一维数组的向量内积。对于更高的维度，它返回最后一个轴上的和的乘积。

14.4 numpy.matmul

numpy.matmul 函数返回两个数组的矩阵乘积。 虽然它返回二维数组的正常乘积，但如果任一参数的维数大于2，则将其视为存在于最后两个索引的矩阵的栈，并进行相应广播。

另一方面，如果任一参数是一维数组，则通过在其维度上附加 1 来将其提升为矩阵，并在乘法之后被去除。

对于二维数组，它就是矩阵乘法

14.5 numpy.linalg.det()

numpy.linalg.det() 函数计算输入矩阵的行列式。

行列式在线性代数中是非常有用的值。 它从方阵的对角元素计算。 对于 2×2 矩阵，它是左上和右下元素的乘积与其他两个的乘积的差。

换句话说，对于矩阵[[a，b]，[c，d]]，行列式计算为 ad-bc。 较大的方阵被认为是 2×2 矩阵的组合。

14.6 numpy.linalg.solve()

numpy.linalg.solve() 函数给出了矩阵形式的线性方程的解。

14.7 numpy.linalg.inv()

numpy.linalg.inv() 函数计算矩阵的乘法逆矩阵。

逆矩阵（inverse matrix）：设A是数域上的一个n阶矩阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA=E ，则我们称B是A的逆矩阵，而A则被称为可逆矩阵。注：E为单位矩阵。