地震正演基础知识
文章目录
- 地震正演
-
- 1. 地震正演基础知识
-
- 1.1 地震波
- 1.2 波动方程
- 1.3 有限差分方法
- 1.4 边界条件
- 1.5 记录数据
- 2. 公式
-
- 2.1 泰勒级数回顾
- 2.2 二维声波方程(连续的偏微分方程)
-
- 2.2.1 二维声波方程(连续的偏微分方程)
- 2.2.2 离散化二维声波方程(差分格式)
- 2.2.2 离散化二维声波方程代码及图像
- 2.3 二维声波方程(一阶速度-应力格式)
-
- 2.3.1 二维声波方程(一阶速度-应力格式)
- 2.3.2 离散化二维声波方程(一阶速度-应力格式)
- 2.3.3 离散化二维声波方程代码及图像
- 2.4 弹性波方程(一阶速度-应力格式)
-
- 2.4.1 弹性波方程(一阶速度-应力格式)
- 2.4.2 离散化弹性波方程(一阶速度-应力格式)
- 2.4.3 离散化弹性波方程代码及图像
地震正演
这篇文章是结合组内师姐培训的地震正演的内容梳理的,若在梳理过程中有问题,欢迎指正!
1. 地震正演基础知识
地震正演模拟是一种以地震波传播理论为基础,在已知地下介质结构的情况下模拟地震波在介质中的传播过程的研究方法.(本次培训讲解的是基于波动方程的微分方程法,微分方程法主要是有限差分法)
1.1 地震波
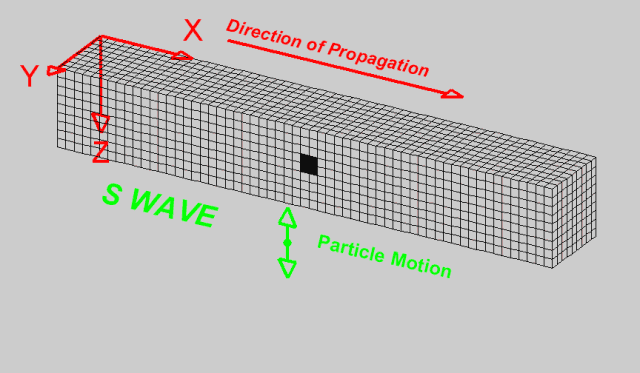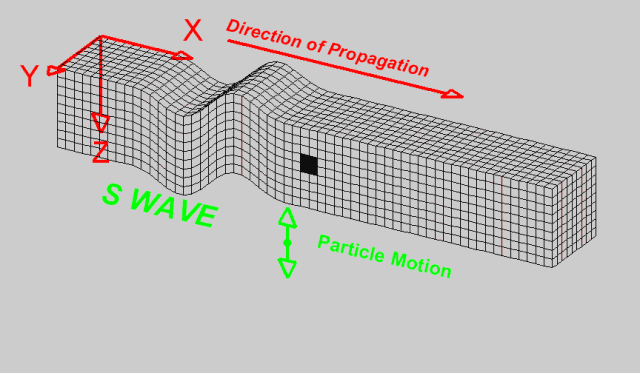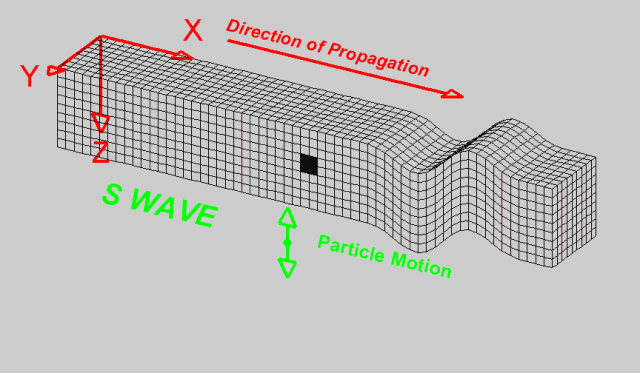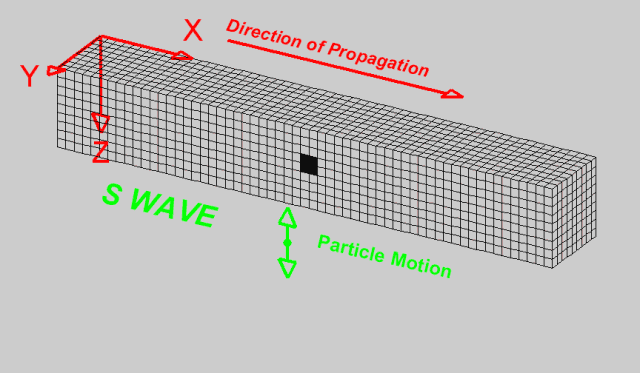
是由地震震源向四处传播的振动,指从震源产生向四周辐射的弹性波。按传播方式可分为纵波(P波)、横波(S波)(纵波和横波均属于体波)和面波(L波)三种类型。 (地震波是弹性波的一种表现形式,它是由地震引起的地球内部应力和应变变化所产生的波动。)
1.2 波动方程
我们在这次的培训中讲解的地震正演模拟是基于波动方程,即描述波在介质中传播的方程。波动方程通常为偏微分方程形式。
1.3 有限差分方法
有限差分方法通过构造截断的泰勒展开式将偏微分方程离散化,进行编程计算,是一种偏微分方程数值求解方法
1.4 边界条件
在地震波传播的数值模拟中,通常会限定计算区域的大小,而计算区域的边界是人为设定的人工边界。为了模拟地震波在有限区域中的传播,需要在计算区域的边界上设置边界条件(目的是减小区域的影响,尽量使边界处的波反射和透射与自然界面的波阻抗差异相似)。
- 吸收边界条件
用于吸收入射波的能量,以避免波的反射和回波干扰计算区域内的波场。例如人工吸收边界或完美匹配层 - 人工边界条件
用于模拟地震波在计算区域边界处的反射和透射现象。如弹性边界
1.5 记录数据
2. 公式
2.1 泰勒级数回顾
泰勒级数展开, 函数 f ( x ) f(x) f(x)在 x 0 x_{0} x0点展开的泰勒级数:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) 1 ! ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . . + f ( n ) x 0 n ! ( x − x 0 ) n + R n (1) f(x) = f(x_0) + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^{2} + .... + \frac{f^{(n)}x_0}{n!}(x-x_0)^{n} + R_{n}\tag 1 f(x)=f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+....+n!f(n)x0(x−x0)n+Rn(1)
其中 R n R_{n} Rn是泰勒公式余项,用于表示泰勒级数展开的两种不同形式的误差项
拉格朗日余项(利用最高阶导数来计算误差):
R n = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) ( n + 1 ) (2) R_{n} = \frac{f^{(n+1)(\xi )}}{(n+1)!}(x-x_0)^{(n+1)}\tag 2 Rn=(n+1)!f(n+1)(ξ)(x−x0)(n+1)(2)
皮亚诺余项(o高阶无穷小):
R n = o ( ( x − x 0 ) n ) (3) R_{n} = o((x-x_0)^n) \tag 3 Rn=o((x−x0)n)(3)
2.2 二维声波方程(连续的偏微分方程)
2.2.1 二维声波方程(连续的偏微分方程)
声波方程是声波在介质中传播的方程, 用于描述声波在空间和时间上的变化。二维声波方程是声波方程在二维平面中的特殊情况。在二维空间中,声波的传播只涉及平面上的两个坐标
1 v 2 ∂ 2 U ∂ t 2 = ∂ 2 U ∂ x 2 + ∂ 2 U ∂ z 2 (4) \frac{1}{v^{2}}\frac{\partial ^{2}U}{\partial t^{2}}=\frac{\partial ^{2}U}{\partial x^{2}} + \frac{\partial ^{2}U}{\partial z^{2}} \tag 4 v21∂t2∂2U=∂x2∂2U+∂z2∂2U(4)
v 表示波速,U 这里我理解为声压(声波的振幅),t 表示时间,x 和 z 分别表示平面上的空间坐标
2.2.2 离散化二维声波方程(差分格式)
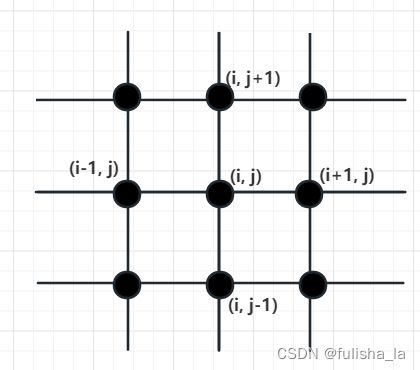
将连续的声波方程转化为离散的差分方程。将二维空间区域离散化为一系列节点 (i, j),在二维差分格式中,声波方程中的导数项和二阶导数项用差分格式进行数值近似。常见的差分格式包括中心差分、向前差分和向后差分
- 中心差分:使用节点的前后点来估计导数的值 例如: f ( i + 1 , j ) − f ( i − 1 , j ) 2 Δ x \frac{f(i+1, j) - f(i-1, j)}{2Δx} 2Δxf(i+1,j)−f(i−1,j)
- 前向差分:使用节点和它后面的点来估计导数的值 例如: f ( i + 1 , j ) − f ( i , j ) Δ x \frac{f(i+1, j) - f(i, j)}{Δx} Δxf(i+1,j)−f(i,j)
- 后向差分:使用节点和它前面的点来估计导数的值 例如: f ( i , j ) − f ( i − 1 , j ) Δ x \frac{f(i, j) - f(i-1, j)}{Δx} Δxf(i,j)−f(i−1,j)
如下:
-
一维空间区域离散化为若干个节点(x0,x1,x2,x3,x4),这些节点之间的距离为网格步长,记为 Δx,用这些离散的点来估计偏导数
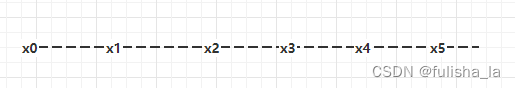
-
利用泰勒级数(式1)对二维声波波动方程进行二阶中心差分格式
函数在x点展开:
f ( x ) − f ( x − h ) = ∂ f ( x ) ∂ x h − 1 2 ∂ f 2 ( x ) ∂ x 2 h 2 + o ( h 2 ) (5) f(x) - f(x-h) = \frac{\partial f(x)}{\partial x}h - \frac{1}{2}\frac{\partial f^{2}(x)}{\partial x^{2}}h^{2}+o(h^{2})\tag 5 f(x)−f(x−h)=∂x∂f(x)h−21∂x2∂f2(x)h2+o(h2)(5)
f ( x + h ) − f ( x ) = ∂ f ( x ) ∂ x h + 1 2 ∂ f 2 ( x ) ∂ x 2 h 2 + o ( h 2 ) (6) f(x+h)-f(x) = \frac{\partial f(x)}{\partial x}h + \frac{1}{2}\frac{\partial f^{2}(x)}{\partial x^{2}}h^{2}+o(h^{2})\tag 6 f(x+h)−f(x)=∂x∂f(x)h+21∂x2∂f2(x)h2+o(h2)(6)
我们是要对二维声波方程进行差分,所以我们要根据泰勒展开后再利用中心差分近似来获得二阶偏导(获取函数在 x 点及其相邻点 x ± h 处的值),则 ( 6 ) − ( 5 ) (6)-(5) (6)−(5)得:
f ( x + h ) + f ( x − h ) − 2 f ( x ) h 2 = ∂ f 2 ( x ) ∂ x 2 + O ( h 2 ) (7) \frac{f(x+h)+f(x-h)-2f(x)}{h^2} = \frac{\partial f^{2}(x)}{\partial x^{2}} + O(h^2)\tag 7 h2f(x+h)+f(x−h)−2f(x)=∂x2∂f2(x)+O(h2)(7)
因为我们是声波方程,我们换一下符号(其中k代表时间层)
∂ 2 U i , j k ∂ x 2 = U i + 1 , j k − 2 U i , j k + U i − 1 , j k Δ x 2 + O ( Δ x ) 2 \frac{\partial ^{2}U_{i,j}^{k}}{\partial x^{2}}=\frac{U_{i+1,j}^{k}-2U_{i,j}^{k} + U_{i-1,j}^{k}}{\Delta x^{2}}+O(\Delta x)^{2} ∂x2∂2Ui,jk=Δx2Ui+1,jk−2Ui,jk+Ui−1,jk+O(Δx)2
∂ 2 U i , j k ∂ z 2 = U i + 1 , j k − 2 U i , j k + U i − 1 , j k Δ z 2 + O ( Δ z ) 2 \frac{\partial ^{2}U_{i,j}^{k}}{\partial z^{2}}=\frac{U_{i+1,j}^{k}-2U_{i,j}^{k} + U_{i-1,j}^{k}}{\Delta z^{2}}+O(\Delta z)^{2} ∂z2∂2Ui,jk=Δz2Ui+1,jk−2Ui,jk+Ui−1,jk+O(Δz)2
∂ 2 U k ∂ t 2 = U k + 1 − 2 U k + U k − 1 Δ t 2 + O ( Δ t ) 2 \frac{\partial ^{2}U^{k}}{\partial t^{2}}=\frac{U^{k+1}-2U^{k} + U^{k-1}}{\Delta t^{2}}+O(\Delta t)^{2} ∂t2∂2Uk=Δt2Uk+1−2Uk+Uk−1+O(Δt)2
结合上面的公式声波波动方程进行近似差分可以得到:
1 v 2 U k + 1 − 2 U k + U k − 1 Δ t 2 = U i + 1 , j k − 2 U i , j k + U i − 1 , j k Δ x 2 + U i + 1 , j k − 2 U i , j k + U i − 1 , j k Δ z 2 (8) \frac{1}{v^2}\frac{U^{k+1}-2U^{k} + U^{k-1}}{\Delta t^{2}} = \frac{U_{i+1,j}^{k}-2U_{i,j}^{k} + U_{i-1,j}^{k}}{\Delta x^{2}} + \frac{U_{i+1,j}^{k}-2U_{i,j}^{k} + U_{i-1,j}^{k}}{\Delta z^{2}}\tag 8 v21Δt2Uk+1−2Uk+Uk−1=Δx2Ui+1,jk−2Ui,jk+Ui−1,jk+Δz2Ui+1,jk−2Ui,jk+Ui−1,jk(8)
这个公式将时间和空间坐标进行离散化,并利用有限差分的形式,近似描述了声波在均匀介质中的传播行为。
可在已知 k及 k − 1 时间层各网格点的声压情况下计算出 k + 1 时间层上各网格点的声压(声波传播的行为是动态的,每个时刻的声波传播状态依赖于前一时刻的状态),可由前一时间层状态求出后一时间层状态,构成了时间上的正序迭代,因此能够通过计算机模拟声波的传播。
2.2.2 离散化二维声波方程代码及图像
结合上面公式的转换为matlab代码(时间上的正序迭代):
% 声波二维均匀模型-中心差分格式
tic
clc
close all
clear all
Endtime=0.5; %模拟时长 单位为秒
delta_t=0.0005;% 时间步长,单位为秒
delta_x=6; %x 方向的空间步长,单位为米
delta_z=6; %z 方向的空间步长,单位为米
CNX=301; %x 方向的网格数
CNZ=301; %z 方向的网格数
v=1500; %波速,单位为米/秒
Sx=(CNX+1)/2; %震源位置的 x 坐标
Sz=(CNZ+1)/2; %震源位置的 z 坐标
f0=30;% 10~40HZ 震源主频
Unow=zeros(CNX,CNZ); % 当前时刻的波场
Uprev=zeros(CNX,CNZ); % 上一时刻的波场
Unext=zeros(CNX,CNZ); % 下一时刻的波场
% 主程序 按时间步长进行迭代
for time=0:delta_t:Endtime
for i=2:CNX-1
for j=2:CNZ-1
% 使用中心差分格式计算二阶导数项
A=(-2*Unow(i,j)+Unow(i+1,j)+Unow(i-1,j))/delta_x^2;
B=(-2*Unow(i,j)+Unow(i,j+1)+Unow(i,j-1))/delta_z^2;
% 使用波动方程的离散形式计算下一时刻的波场值
Unext(i,j)=2*Unow(i,j)-Uprev(i,j)+v^2*(A+B)*delta_t^2;
end
end
% 设置震源的激励函数,这里使用的是高斯脉冲函数
Unext(Sx,Sz)=5.76*f0^2*(1-16*(0.6*f0*time-1)^2)*exp(-8*(0.6*f0*time-1)^2);%震源函数
Uprev=Unow; % 更新波场,当前时刻变为上一时刻
Unow=Unext; % 更新波场,下一时刻变为当前时刻
end
%绘图
surf(Unow)
shading interp;
view(2);%view(90,90)
colormap(gray);
toc
- 上面是通过二阶中心差分来离散化二维声波方程,可以通过三阶中心差分来离散化二维声波方程可以更准确地逼近二阶空间导数。其离散后的公式为:
1 v 2 U k + 1 − 2 U k + U k − 1 Δ t 2 = c 1 U i + 1 , j k − 2 U i , j k + U i − 1 , j k Δ x 2 + c 1 U i , j + 1 k − 2 U i , j k + U i , j − 1 k Δ z 2 + c 2 U i + 2 , j k − 2 U i , j k + U i − 2 , j k 4 Δ x 2 + c 2 U i , j + 2 k − 2 U i , j k + U i , j − 2 k 4 Δ z 2 + c 3 U i + 3 , j k − 2 U i , j k + U i − 3 , j k 9 Δ x 2 + c 3 U i , j + 3 k − 2 U i , j k + U i , j − 3 k 9 Δ z 2 + O ( Δ x 6 ) \frac{1}{v^2}\frac{U^{k+1}-2U^{k} + U^{k-1}}{\Delta t^{2}} = c_{1}\frac{U_{i+1,j}^{k}-2U_{i,j}^{k} + U_{i-1,j}^{k}}{\Delta x^{2}} + c_{1}\frac{U_{i,j+1}^{k}-2U_{i,j}^{k} + U_{i,j-1}^{k}}{\Delta z^{2}} + c_{2}\frac{U_{i+2,j}^{k}-2U_{i,j}^{k} + U_{i-2,j}^{k}}{4 \Delta x^{2}}+c_{2}\frac{U_{i,j+2}^{k}-2U_{i,j}^{k} + U_{i,j-2}^{k}}{4 \Delta z^{2}}+c_{3}\frac{U_{i+3,j}^{k}-2U_{i,j}^{k} + U_{i-3,j}^{k}}{9 \Delta x^{2}} +c_{3}\frac{U_{i,j+3}^{k}-2U_{i,j}^{k} + U_{i,j-3}^{k}}{9 \Delta z^{2}} +O(\Delta x^{6}) v21Δt2Uk+1−2Uk+Uk−1=c1Δx2Ui+1,jk−2Ui,jk+Ui−1,jk+c1Δz2Ui,j+1k−2Ui,jk+Ui,j−1k+c24Δx2Ui+2,jk−2Ui,jk+Ui−2,jk+c24Δz2Ui,j+2k−2Ui,jk+Ui,j−2k+c39Δx2Ui+3,jk−2Ui,jk+Ui−3,jk+c39Δz2Ui,j+3k−2Ui,jk+Ui,j−3k+O(Δx6)
注:这也是培训过程的作业,我当时的思路是这样的(虽然和最后推出来还是有出入):因为我们二维声波方程的离散化是对泰勒级数到二阶就进行截取,而这里的三阶中心差分,我们是将泰勒级数展开到三阶再进行截取,自然他的误差就要比二阶小一点(过程太复杂了,知道思路就好…)。
所以他的代码(并且加入了添加边界的代码)
% 声波二阶-添加边界-常规网格
tic
clc
close all
clear all
Endtime=0.8; %模拟时长
delta_t=0.001;%以秒为单位
delta_x=0.006;%以千米为单位 空间步长
delta_z=0.006;
f0=30;% 10~40HZ 震源频率
iteration=1;
nk=1;
n=Endtime/delta_t;
CNX=301; %
CNZ=301; %
BNX=20;
BNZ=20;
XMAX=CNX+2*BNX;
ZMAX=CNZ+2*BNZ;
Sx=(XMAX+1)/2; %震源位置
Sz=(ZMAX+1)/2;
c=0;
%zeros(XMAX,ZMAX);%波速
v(1:100,1:ZMAX)=2.0;
v(101:200,1:ZMAX)=2.0;
v(201:XMAX,1:ZMAX)=2;
a=-0.15;
S=0.001;
Wave=zeros(n+1,1);
Fnow=zeros(n+1,CNZ);
Unow=zeros(XMAX,ZMAX);
Uprev=zeros(XMAX,ZMAX);
Unext=zeros(XMAX,ZMAX);
Uxnow=zeros(XMAX,ZMAX);%n
Uxprev=zeros(XMAX,ZMAX);%n-1
Uxnext=zeros(XMAX,ZMAX);%n+1
Uznow=zeros(XMAX,ZMAX);%n
Uzprev=zeros(XMAX,ZMAX);%n-1
Uznext=zeros(XMAX,ZMAX);%n+1
Psi2x=zeros(2*BNZ,XMAX);
Uxxprev=zeros(2*BNZ,XMAX);
Psi2xprev=zeros(2*BNZ,XMAX);
Eta2xprev=zeros(2*BNZ,XMAX);
Eta2x=zeros(2*BNZ,XMAX);
Psixprev=zeros(2*BNZ,XMAX);
Psix=zeros(2*BNZ,XMAX);
Etaxprev=zeros(2*BNZ,XMAX);
Etax=zeros(2*BNZ,XMAX);
Thetaxprev=zeros(2*BNZ,XMAX);
Thetax=zeros(2*BNZ,XMAX);
Uzzprev=zeros(ZMAX,2*BNZ);
Psi2zprev=zeros(ZMAX,2*BNZ);
Psi2z=zeros(ZMAX,2*BNZ);
Eta2zprev=zeros(ZMAX,2*BNZ);
Eta2z=zeros(ZMAX,2*BNZ);
Psizprev=zeros(ZMAX,2*BNZ);
Psiz=zeros(ZMAX,2*BNZ);
Etazprev=zeros(ZMAX,2*BNZ);
Etaz=zeros(ZMAX,2*BNZ);
Thetazprev=zeros(ZMAX,2*BNZ);
Thetaz=zeros(ZMAX,2*BNZ);
% 主程序
for time=0:delta_t:Endtime
for m=4:XMAX-3
for n=4:ZMAX-3
c=v(m,n);
%A=(-2*Unow(m,n)+Unow(m+1,n)+Unow(m-1,n))/delta_x^2;
%B=(-2*Unow(m,n)+Unow(m,n+1)+Unow(m,n-1))/delta_z^2;
A=(-2.8194*Unow(m,n)+1.575*(Unow(m+1,n)+Unow(m-1,n))-0.1827*(Unow(m+2,n)+Unow(m-2,n))+0.0174*(Unow(m+3,n)+Unow(m-3,n)))/delta_x^2;
B=(-2.8194*Unow(m,n)+1.575*(Unow(m,n+1)+Unow(m,n-1))-0.1827*(Unow(m,n+2)+Unow(m,n-2))+0.0174*(Unow(m,n+3)+Unow(m,n-3)))/delta_z^2;
Unext(m,n)=2*Unow(m,n)-Uprev(m,n)+c^2*(A+B)*delta_t^2;
%fprintf('their is %8.5f\n',c);
%***************添加边界***************
if m<=BNX+1 || m>=BNX+CNX || n<=BNZ+1 || n>=BNZ+CNZ
Uxx=A;
Uzz=B;
%U的X方向****************************
if m<=BNX+1 || m>=CNX+BNX
if m<=BNX+1
XBPos=m;
XBDistance=(BNX+1-m)*delta_x;
else
XBPos=m-CNX;
XBDistance=(m-(BNX+CNX))*delta_x;
end
ZBPos=n;
XBThick=BNX*delta_x ;
XDecay=-3*c*log(S)/(2*XBThick)*(XBDistance/XBThick)^2;
XDecay_order=-3*c*log(S)*XBDistance/XBThick^3;
XAlpha=pi*f0*(1-XBDistance/XBThick);
XAlpha_order=-pi*f0/XBThick;
bX=exp(-(XDecay+XAlpha)*delta_t);
aX=(1-bX)/(XDecay+XAlpha);
%傅里叶逆变换各部分表达式
Psi2x(XBPos,ZBPos)=bX*Psi2xprev(XBPos,ZBPos)+aX*0.5*(Uxx+Uxxprev(XBPos,ZBPos));
Eta2x(XBPos,ZBPos)=bX*Eta2xprev(XBPos,ZBPos)+aX*0.5*(Psi2x(XBPos,ZBPos)+Psi2xprev(XBPos,ZBPos));
Psix(XBPos,ZBPos)=bX*Psixprev(XBPos,ZBPos)+aX*0.5*(Uxnow(m,n)+Uxprev(m,n));
Etax(XBPos,ZBPos)=bX*Etaxprev(XBPos,ZBPos)+aX*0.5*(Psix(XBPos,ZBPos)+Psixprev(XBPos,ZBPos)) ;
Thetax(XBPos,ZBPos)=bX*Thetaxprev(XBPos,ZBPos)+aX*0.5*(Etax(XBPos,ZBPos)+Etaxprev(XBPos,ZBPos)) ;
%指标变换——迭代更新
Uxxprev(XBPos,ZBPos)=Uxx;
Psi2xprev(XBPos,ZBPos)=Psi2x(XBPos,ZBPos);
Eta2xprev(XBPos,ZBPos)=Eta2x(XBPos,ZBPos);
Psixprev(XBPos,ZBPos)=Psix(XBPos,ZBPos);
Etaxprev(XBPos,ZBPos)=Etax(XBPos,ZBPos);
Thetaxprev(XBPos,ZBPos)=Thetax(XBPos,ZBPos);
%U的X方向二阶偏导数的傅里叶逆变换表达式
Uxx=Uxx-2*XDecay*Psi2x(XBPos,ZBPos)+XDecay^2*Eta2x(XBPos,ZBPos)-XDecay_order*Psix(XBPos,ZBPos)...
+XDecay*(2*XDecay_order+XAlpha_order)*Etax(XBPos,ZBPos)-XDecay^2*(XDecay_order+XAlpha_order)*Thetax(XBPos,ZBPos);
end
% **************U的Z方向****************************
if n<=BNZ+1 || n>=BNZ+CNZ
if n<=BNZ+1
ZBPos=n;
ZBDistance=(BNZ+1-n)*delta_z;
else
ZBPos=n-CNZ;
ZBDistance=(n-(BNZ+CNZ))*delta_z;
end
XBPos=m;
ZBThick=BNZ*delta_z;
ZDecay=-3*c/(2*ZBThick)*log(S)*(ZBDistance/ZBThick)^2;
ZDecay_order=-3*c*log(S)*ZBDistance/ZBThick^3;
ZAlpha=pi*f0*(1-ZBDistance/ZBThick);
ZAlpha_order=-pi*f0/ZBThick;
bZ=exp(-(ZDecay+ZAlpha)*delta_t);
aZ=(1-bZ)/(ZDecay+ZAlpha);
%傅里叶逆变换各部分表达式
Psi2z(XBPos,ZBPos)=bZ*Psi2zprev(XBPos,ZBPos)+aZ*0.5*(Uzz+Uzzprev(XBPos,ZBPos));
Eta2z(XBPos,ZBPos)=bZ*Eta2zprev(XBPos,ZBPos)+aZ*0.5*(Psi2z(XBPos,ZBPos)+Psi2zprev(XBPos,ZBPos));
Psiz(XBPos,ZBPos)=bZ*Psizprev(XBPos,ZBPos)+aZ*0.5*(Uznow(m,n)+Uzprev(m,n));
Etaz(XBPos,ZBPos)=bZ*Etazprev(XBPos,ZBPos)+aZ*0.5*(Psiz(XBPos,ZBPos)+Psizprev(XBPos,ZBPos)) ;
Thetaz(XBPos,ZBPos)=bZ*Thetazprev(XBPos,ZBPos)+aZ*0.5*(Etaz(XBPos,ZBPos)+Etazprev(XBPos,ZBPos)) ;
%指标变换——迭代更新
Uzzprev(XBPos,ZBPos)=Uzz;
Psi2zprev(XBPos,ZBPos)=Psi2z(XBPos,ZBPos);
Eta2zprev(XBPos,ZBPos)=Eta2z(XBPos,ZBPos);
Psizprev(XBPos,ZBPos)=Psiz(XBPos,ZBPos);
Etazprev(XBPos,ZBPos)=Etaz(XBPos,ZBPos);
Thetazprev(XBPos,ZBPos)=Thetaz(XBPos,ZBPos);
%Z方向二阶偏导数的傅里叶逆变换表达式
Uzz=Uzz-2*ZDecay*Psi2z(XBPos,ZBPos)+ZDecay^2*Eta2z(XBPos,ZBPos)-ZDecay_order*Psiz(XBPos,ZBPos)...
+ZDecay*(2*ZDecay_order+ZAlpha_order)*Etaz(XBPos,ZBPos)-ZDecay^2*(ZDecay_order+ZAlpha_order)*Thetaz(XBPos,ZBPos);
end
Unext(m,n)=2*Unow(m,n)-Uprev(m,n)+(c*delta_t)^2*(Uxx+Uzz);
end %边界循环结束
if m == Sx
Fnow(nk,n) = Unext(Sx,n);%地震记录
end
Wave(iteration) = Unext(101,151); %波形图
iteration = iteration + 1;
end
end
Unext(Sx,Sz)=delta_t^2*5.76*f0^2*(1-16*(0.6*f0*time-1)^2)*exp(-8*(0.6*f0*time-1)^2);
Uprev=Unow; %波场更新
Unow=Unext;
nk=nk+1;
end
%绘图
%plot(Wave)
%surf(Unow)
surf(Fnow)
shading interp;
view(2);%view(90,90)
colormap(gray);
toc
我把模拟时长设置为0.8,就能明显感受到加入和没加入边界的效果。
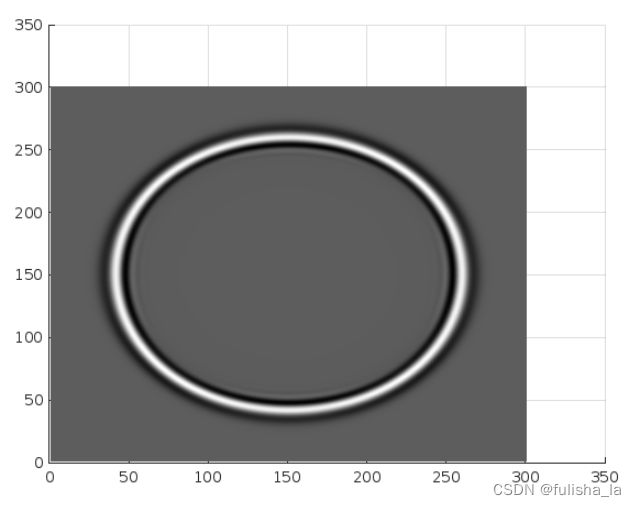
下面是加了边界处理的图像:
(添加边界处理,可以更准确地模拟波场在有限域内的传播,避免了边界的影响对波场造成的不良影响)
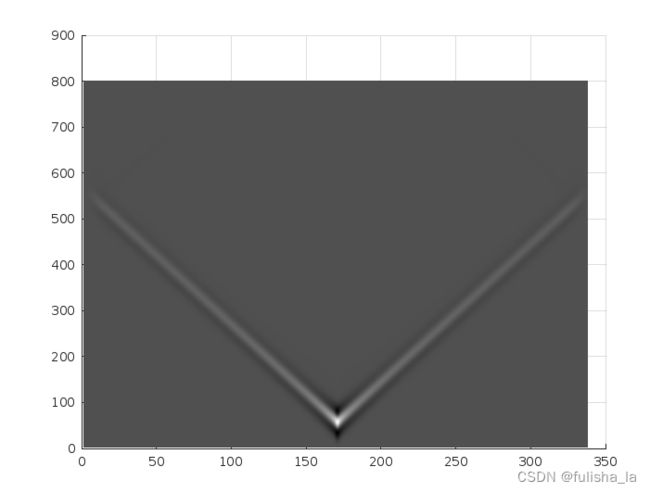
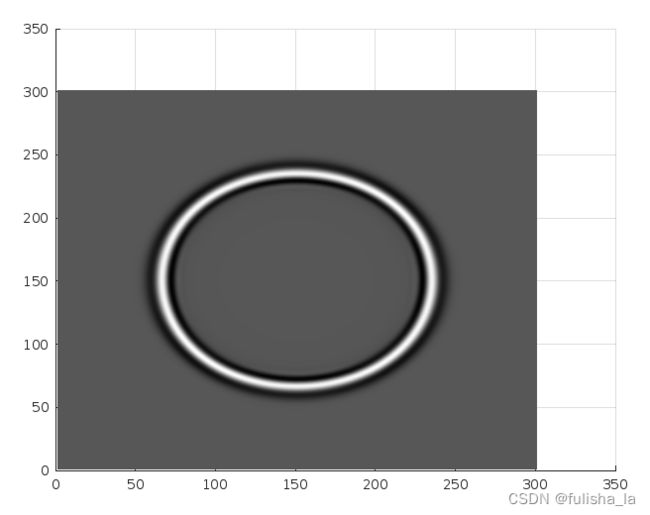
去掉边界处理的图像:
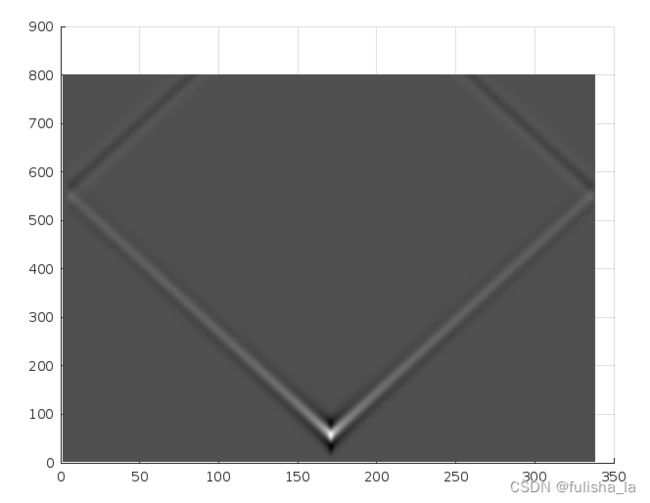
2.3 二维声波方程(一阶速度-应力格式)
2.3.1 二维声波方程(一阶速度-应力格式)
{ ∂ v x ∂ t = 1 ρ ∂ P ∂ x ∂ v z ∂ t = 1 ρ ∂ P ∂ y ∂ P ∂ t = ρ v 2 ( ∂ v x ∂ x + ∂ v z ∂ y ) (9) \begin{cases} \frac{ \partial v_{x}}{\partial t} = \frac{1}{\rho }\frac{\partial P}{\partial x} \\ \frac{ \partial v_{z}}{\partial t} = \frac{1}{\rho }\frac{\partial P}{\partial y} \\ \frac{ \partial P}{\partial t} = \rho v^{2}(\frac{\partial v _{x}}{\partial x} +\frac{ \partial v_{z}}{\partial y} ) \\ \end{cases} \tag{9} ⎩ ⎨ ⎧∂t∂vx=ρ1∂x∂P∂t∂vz=ρ1∂y∂P∂t∂P=ρv2(∂x∂vx+∂y∂vz)(9)
2.3.2 离散化二维声波方程(一阶速度-应力格式)
交错网格:
交错网格差分方法主要用于处理具有复杂几何形状的区域或介质边界的问题,在声波传播问题中,交错网格差分可以更好地处理波的反射和折射等现象。
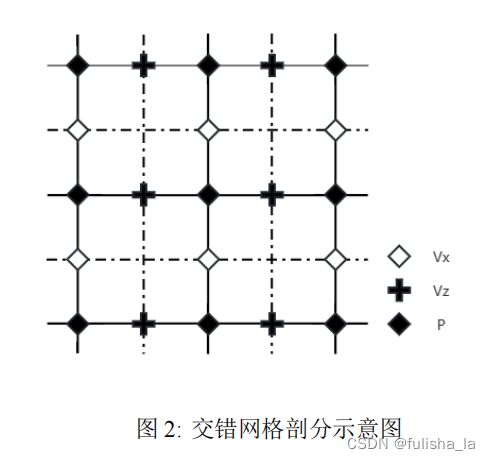
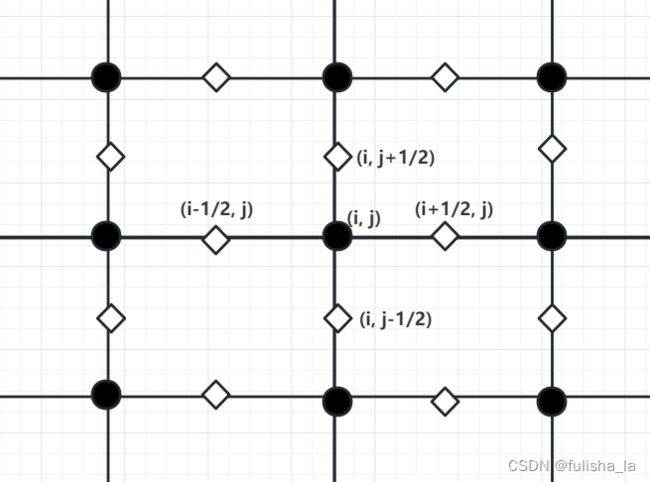
(这里的交错点不一定非得在中心)
同样用泰勒级数展开去化解(式子5和式子6)但我们需要保留的是一阶格式,而不是二阶
f ( x + h ) − f ( x − h ) 2 h = ∂ f ( x ) ∂ x + O ( h ) (10) \frac{f(x+h) - f(x-h)}{2h} = \frac{\partial f(x)}{\partial x}+O(h) \tag{10} 2hf(x+h)−f(x−h)=∂x∂f(x)+O(h)(10)
P i + 1 2 , j k P_{i+\frac{1}{2},j}^{k} Pi+21,jk 和 P i − 1 2 , j k P_{i-\frac{1}{2},j}^{k} Pi−21,jk 是在 x x x 方向上相邻格点处的声压值, Δ x \Delta x Δx 是空间步长,声压 P 关于空间 x 方向的偏导数 (声压在空间 x 方向上的变化):
∂ P i , j k ∂ x = P i + 1 2 , j k − P i − 1 2 , j k Δ x + O ( Δ x ) \frac{\partial P_{i,j}^{k}}{\partial x}=\frac{P_{i+\frac{1}{2},j}^{k} - P_{i-\frac{1}{2},j}^{k}}{\Delta x} + O(\Delta x) ∂x∂Pi,jk=ΔxPi+21,jk−Pi−21,jk+O(Δx)
声压 P 关于空间 z 方向的偏导数(声压在空间 z 方向上的变化):
∂ P i , j k ∂ z = P i , j + 1 2 k − P i , j − 1 2 k Δ z + O ( Δ z ) \frac{\partial P_{i,j}^{k}}{\partial z}=\frac{P_{i,j+\frac{1}{2}}^{k} - P_{i,j-\frac{1}{2}}^{k}}{\Delta z} + O(\Delta z) ∂z∂Pi,jk=ΔzPi,j+21k−Pi,j−21k+O(Δz)
P i , j k + 1 P_{i,j}^{k+1} Pi,jk+1 和 P i , j k P_{i,j}^{k} Pi,jk 是在时间上相邻时刻的声压值, Δ t \Delta t Δt 是时间步长(声波在时间上的变化)
∂ P i , j k ∂ t = P i , j k + 1 − P i , j k Δ t + O ( Δ t ) \frac{\partial P_{i,j}^{k}}{\partial t}=\frac{P_{i,j}^{k+1} - P_{i,j}^{k} }{\Delta t} + O(\Delta t) ∂t∂Pi,jk=ΔtPi,jk+1−Pi,jk+O(Δt)
速度分量 U 关于空间 x 方向的偏导数(速度在空间 x 方向上的变化):
∂ U i , j k ∂ x = U i + 1 2 , j k − U i − 1 2 , j k Δ x + O ( Δ z ) \frac{\partial U_{i,j}^{k}}{\partial x}=\frac{U_{i+\frac{1}{2},j}^{k} - U_{i-\frac{1}{2},j}^{k}}{\Delta x} + O(\Delta z) ∂x∂Ui,jk=ΔxUi+21,jk−Ui−21,jk+O(Δz)
速度分量 V 关于空间 z 方向的偏导数(速度在空间 z 方向上的变化):
∂ V i , j k ∂ z = V i , j + 1 2 k − U i , j − 1 2 k Δ z + O ( Δ z ) \frac{\partial V_{i,j}^{k}}{\partial z}=\frac{V_{i,j+\frac{1}{2}}^{k} - U_{i,j-\frac{1}{2}}^{k}}{\Delta z} + O(\Delta z) ∂z∂Vi,jk=ΔzVi,j+21k−Ui,j−21k+O(Δz)
所以化解后的声波波动方程:
{ U i , j k + 1 − U i , j k Δ t = 1 ρ P i + 1 2 , j k − P i − 1 2 , j k Δ x V i , j k + 1 − V i , j k Δ t = 1 ρ P i , j + 1 2 k − P i , j − 1 2 k Δ z P i , j k + 1 − P i , j k Δ t = ρ v 2 ( U i + 1 2 , j k + 1 − U i − 1 2 , j k + 1 Δ x + V i , j + 1 2 k + 1 − V i , j − 1 2 k + 1 Δ z ) (11) \begin{cases} \frac{U_{i,j}^{k+1} - U_{i,j}^{k} }{\Delta t} = \frac{1}{\rho }\frac{P_{i+\frac{1}{2},j}^{k} - P_{i-\frac{1}{2},j}^{k}}{\Delta x} \\ \frac{V_{i,j}^{k+1} - V_{i,j}^{k}}{\Delta t} = \frac{1}{\rho }\frac{P_{i,j+\frac{1}{2}}^{k} - P_{i,j-\frac{1}{2}}^{k}}{\Delta z} \\ \frac{P_{i,j}^{k+1} - P_{i,j}^{k}}{\Delta t} =\rho v^{2}(\frac{U_{i+\frac{1}{2},j}^{k+1} - U_{i-\frac{1}{2},j}^{k+1}}{\Delta x} + \frac{V_{i,j+\frac{1}{2}}^{k+1} - V_{i,j-\frac{1}{2}}^{k+1}}{\Delta z}) \\ \tag{11} \end{cases} ⎩ ⎨ ⎧ΔtUi,jk+1−Ui,jk=ρ1ΔxPi+21,jk−Pi−21,jkΔtVi,jk+1−Vi,jk=ρ1ΔzPi,j+21k−Pi,j−21kΔtPi,jk+1−Pi,jk=ρv2(ΔxUi+21,jk+1−Ui−21,jk+1+ΔzVi,j+21k+1−Vi,j−21k+1)(11)
2.3.3 离散化二维声波方程代码及图像
其中的matlab代码:
% 声波二维_一阶速度-应力格式_交错网格
tic
clc
close all
clear all
Endtime=0.4; %模拟时长
delta_t=0.0005;%以秒为单位
delta_x=0.008;%以千米为单位 空间步长
delta_z=0.008;
CNX=301; %x方向的网格数
CNZ=301; %
rho=1.2;%
v=2; %波速
Sx=(CNX+1)/2; %震源位置
Sz=(CNZ+1)/2;
f0=30;% 10~40HZ 震源频率
Unow=zeros(CNX,CNZ);
Unext=zeros(CNX,CNZ);
Vnow=zeros(CNX,CNZ);
Vnext=zeros(CNX,CNZ);
Pnow=zeros(CNX,CNZ);
Pnext=zeros(CNX,CNZ);
% 主程序
for time=0:delta_t:Endtime
for i=2:CNX-1
for j=2:CNZ-1
M=(Pnow(i,j)-Pnow(i-1,j))/(rho*delta_x);
N=(Pnow(i,j)-Pnow(i,j-1))/(rho*delta_z);
Unext(i,j) = Unow(i,j) + delta_t*M;
Vnext(i,j) = Vnow(i,j) + delta_t*N;
end
end
for i=1:CNX-1
for j=1:CNZ-1
X = (Unext(i+1,j) - Unext(i,j))/delta_x;
Y = (Vnext(i,j+1) - Vnext(i,j))/delta_z;
Pnext(i,j)=Pnow(i,j) + rho*v*v*(X+Y)*delta_t;
end
end
Pnext(Sx,Sz)=5.76*f0^2*(1-16*(0.6*f0*time-1)^2)*exp(-8*(0.6*f0*time-1)^2);
%波场更新
Unow=Unext; %波场更新
Vnow=Vnext; %波场更新
Pnow=Pnext;
end
% max(max(Vnext))
%绘图
surf(Pnow)
%surf(Unow)%x方向速度分量
%surf(Vnow)%z方向速度分量
shading interp;
view(2);%view(90,90)
colormap(gray);
toc
2.4 弹性波方程(一阶速度-应力格式)
2.4.1 弹性波方程(一阶速度-应力格式)
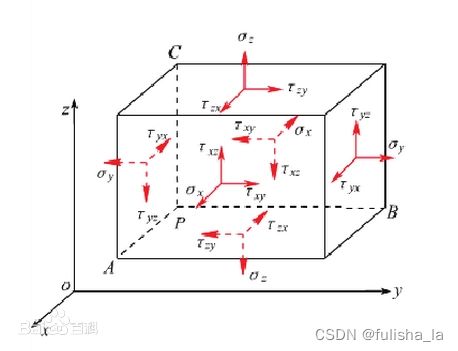
{ ρ ∂ v x ∂ t = ∂ τ x x ∂ x + ∂ τ x z ∂ z ρ ∂ v z ∂ t = ∂ τ x z ∂ x + ∂ τ z z ∂ z ρ τ x x ∂ t = c 11 ∂ v x ∂ x + c 13 ∂ v z ∂ z ρ τ z z ∂ t = c 13 ∂ v x ∂ x + c 33 ∂ v z ∂ z ρ τ x z ∂ t = c 44 ∂ v z ∂ x + c 44 ∂ v x ∂ z (12) \begin{cases} \rho \frac{\partial v_{x}}{\partial t} = \frac{\partial \tau_{xx}}{\partial x} + \frac{\partial \tau_{xz}}{\partial z} \\ \rho \frac{\partial v_{z}}{\partial t} = \frac{\partial \tau_{xz}}{\partial x} + \frac{\partial \tau_{zz}}{\partial z} \\ \rho \frac{\tau_{xx}}{\partial t} = c_{11} \frac{\partial v_x}{\partial x} + c_{13}\frac{\partial v_z}{\partial z}\\ \rho \frac{\tau_{zz}}{\partial t} = c_{13} \frac{\partial v_x}{\partial x} + c_{33}\frac{\partial v_z}{\partial z}\\ \rho \frac{\tau_{xz}}{\partial t} = c_{44} \frac{\partial v_z}{\partial x} + c_{44}\frac{\partial v_x}{\partial z}\\ \end{cases} \tag{12} ⎩ ⎨ ⎧ρ∂t∂vx=∂x∂τxx+∂z∂τxzρ∂t∂vz=∂x∂τxz+∂z∂τzzρ∂tτxx=c11∂x∂vx+c13∂z∂vzρ∂tτzz=c13∂x∂vx+c33∂z∂vzρ∂tτxz=c44∂x∂vz+c44∂z∂vx(12)
- 其中 τ \tau τ是应力,(由于外因(受力、湿度、温度场变化等)而变形时,在物体内各部分之间产生相互作用的内力,单位面积上的内力称为应力——百度百科),应力有两种类型:正应力–正应力垂直于给定面的方向;剪切应力–剪切应力平行于给定面的方向,例如 τ x x \tau_{xx} τxx作用在 x 方向平面上的垂直应力, τ y y \tau_{yy} τyy作用在y 方向平面上的垂直应力; τ x y \tau_{xy} τxy作用在 x-y 平面上的切变应力
2.4.2 离散化弹性波方程(一阶速度-应力格式)
同理,我们也采用泰勒级数近似差分转换上面的式子(结合式11和上面声波方程的化解)
其中速度分量 U、V 和应力分量 R、T、H。
{ ρ U i , j k + 1 − U i , j k Δ t = R i + 1 2 , j k − R i − 1 2 , j k Δ x + H i , j + 1 2 k − H i , j − 1 2 k Δ z [1] ρ V i , j k + 1 − V i , j k Δ t = H i + 1 2 , j k − H i − 1 2 , j k Δ x + T i , j + 1 2 k − T i , j − 1 2 k Δ z [2] R i , j k + 1 − R i , j k Δ t = c 11 U i + 1 2 , j k + 1 − U i − 1 2 , j k + 1 Δ x + c 13 V i , j + 1 2 k + 1 − V i , j − 1 2 k + 1 Δ z [3] T i , j k + 1 − T i , j k Δ t = c 13 U i + 1 2 , j k + 1 − U i − 1 2 , j k + 1 Δ x + c 33 V i , j + 1 2 k + 1 − V i , j − 1 2 k + 1 Δ z [4] H i , j k + 1 − H i , j k Δ t = c 44 V i + 1 2 , j k + 1 − V i − 1 2 , j k + 1 Δ x + c 44 U i , j + 1 2 k + 1 − U i , j − 1 2 k + 1 Δ z [5] (13) \begin{cases} \rho \frac{U_{i,j}^{k+1} - U_{i,j}^{k} }{\Delta t} = \frac{R_{i+\frac{1}{2},j}^{k} - R_{i-\frac{1}{2},j}^{k}}{\Delta x} + \frac{H_{i,j+\frac{1}{2}}^{k} - H_{i,j-\frac{1}{2}}^{k}}{\Delta z} & \text {[1]}\\ \rho \frac{V_{i,j}^{k+1} - V_{i,j}^{k} }{\Delta t} = \frac{H_{i+\frac{1}{2},j}^{k} - H_{i-\frac{1}{2},j}^{k}}{\Delta x} + \frac{T_{i,j+\frac{1}{2}}^{k} - T_{i,j-\frac{1}{2}}^{k}}{\Delta z}& \text {[2]}\\ \frac{R_{i,j}^{k+1} - R_{i,j}^{k} }{\Delta t} = c_{11}\frac{U_{i+\frac{1}{2},j}^{k+1} - U_{i-\frac{1}{2},j}^{k+1}}{\Delta x} + c_{13} \frac{V_{i,j+\frac{1}{2}}^{k+1} - V_{i,j-\frac{1}{2}}^{k+1}}{\Delta z}& \text {[3]}\\ \frac{T_{i,j}^{k+1} - T_{i,j}^{k} }{\Delta t} = c_{13}\frac{U_{i+\frac{1}{2},j}^{k+1} - U_{i-\frac{1}{2},j}^{k+1}}{\Delta x} + c_{33} \frac{V_{i,j+\frac{1}{2}}^{k+1} - V_{i,j-\frac{1}{2}}^{k+1}}{\Delta z}& \text {[4]}\\ \frac{H_{i,j}^{k+1} - H_{i,j}^{k} }{\Delta t} = c_{44}\frac{V_{i+\frac{1}{2},j}^{k+1} - V_{i-\frac{1}{2},j}^{k+1}}{\Delta x} + c_{44} \frac{U_{i,j+\frac{1}{2}}^{k+1} - U_{i,j-\frac{1}{2}}^{k+1}}{\Delta z}& \text {[5]}\\ \end{cases} \tag{13} ⎩ ⎨ ⎧ρΔtUi,jk+1−Ui,jk=ΔxRi+21,jk−Ri−21,jk+ΔzHi,j+21k−Hi,j−21kρΔtVi,jk+1−Vi,jk=ΔxHi+21,jk−Hi−21,jk+ΔzTi,j+21k−Ti,j−21kΔtRi,jk+1−Ri,jk=c11ΔxUi+21,jk+1−Ui−21,jk+1+c13ΔzVi,j+21k+1−Vi,j−21k+1ΔtTi,jk+1−Ti,jk=c13ΔxUi+21,jk+1−Ui−21,jk+1+c33ΔzVi,j+21k+1−Vi,j−21k+1ΔtHi,jk+1−Hi,jk=c44ΔxVi+21,jk+1−Vi−21,jk+1+c44ΔzUi,j+21k+1−Ui,j−21k+1[1][2][3][4][5](13)
- [1] 描述U 速度分量的时间变化与 R 正应力分量和 H 剪切应力分量在 x 和 z 方向上的梯度之间的关系(变化率)
- [2] V 速度分量的时间变化与 H 剪切应力分量和 T 正应力分量在 x 和 z 方向上的梯度之间的关系
- [3]描述了 R 正应力分量的时间变化与 U 速度分量在 x 方向和 V 速度分量在 z 方向上的梯度之间的关系
- [4]描述了 T 正应力分量的时间变化与 U 速度分量在 x 方向和 V 速度分量在 z 方向上的梯度之间的关系
- [5]描述了 H 剪切应力分量的时间变化与 V 速度分量在 x 方向和 U 速度分量在 z 方向上的梯度之间的关系
2.4.3 离散化弹性波方程代码及图像
matlab代码-(对应他离散化的格式):下面
% 正演编程
%二维各向同性均匀介质弹性波_空间二阶时间二阶
tic % 开始计时
clc % 清空命令窗口
close all % 关闭所有图形窗口
clear all % 清除工作区的所有变量
Endtime=0.3; %模拟时长
delta_t=0.001;% 时间步长,单位:秒
delta_x=0.004;% 空间步长,单位:千米
delta_z=0.004;
CNX=401; % x 方向的网格数
CNZ=401; % z 方向的网格数
rho=2.0; % 密度
Sx=(CNX+1)/2; % 震源位置的 x 坐标
Sz=(CNZ+1)/2; % 震源位置的 z 坐标
f0=40;% 10~40HZ 震源频率
lambda=3.5; % Lame 参数 lambda
mu=3; % Lame 参数 mu
c11=lambda+2*mu; % 弹性系数 c11
c13=lambda; % 弹性系数 c13
c33=lambda+2*mu; % 弹性系数 c33
c44=mu; % 弹性系数 c44
%vp=2.32 vs=1.3
Rnow=zeros(CNX,CNZ); % 当前时刻的正应力分量 R
Rnext=zeros(CNX,CNZ); % 下一个时刻的正应力分量 R
Hnow=zeros(CNX,CNZ); % 当前时刻的剪切应力分量 H
Hnext=zeros(CNX,CNZ); % 下一个时刻的剪切应力分量 H
Tnow=zeros(CNX,CNZ); % 当前时刻的正应力分量 T
Tnext=zeros(CNX,CNZ); % 下一个时刻的正应力分量 T
Unow=zeros(CNX,CNZ); % 当前时刻的 x 方向速度分量 U
Unext=zeros(CNX,CNZ); % 下一个时刻的 x 方向速度分量 U
Vnow=zeros(CNX,CNZ); % 当前时刻的 z 方向速度分量 V
Vnext=zeros(CNX,CNZ); % 下一个时刻的 z 方向速度分量 V
% 主程序
for time=0:delta_t:Endtime % 时间迭代循环
% x 和 z 方向上的空间迭代
for i=2:CNX-1
for j=2:CNZ-1
% 计算速度分量的时间变化量 delta_u 和 delta_v
X1 = Rnow(i+1,j) - Rnow(i,j);
Y1x = Hnow(i,j) - Hnow(i,j-1);
Y1z = Hnow(i,j) - Hnow(i-1,j);
Z1 = Tnow(i,j+1) - Tnow(i,j);
delta_u = (X1+Y1x)*delta_t/(rho*delta_x);
Unext(i,j)=Unow(i,j) + delta_u;
delta_v = (Y1z+Z1)*delta_t/(rho*delta_z);
Vnext(i,j)=Vnow(i,j) + delta_v;
end
end
% x 和 z 方向上的空间迭代
for i=2:CNX-1
for j=2:CNZ-1
% 计算应力分量的时间变化量 delta_r、delta_tn 和 delta_h
M1 = Unext(i,j) - Unext(i-1,j);
Mn1 = Unext(i,j+1) - Unext(i,j);
N1 = Vnext(i,j) - Vnext(i,j-1);
Nm1 = Vnext(i+1,j) - Vnext(i,j);
delta_r = delta_t*(c11*M1+c13*N1)/delta_x;
Rnext(i,j) = Rnow(i,j) + delta_r;
delta_tn = delta_t*(c13*M1+c33*N1)/delta_x;
Tnext(i,j) = Tnow(i,j) + delta_tn;
delta_h = delta_t*(c44*Mn1+c44*Nm1)/delta_x;
Hnext(i,j) = Hnow(i,j) + delta_h;
end
end
Unext(Sx,Sz)=Unext(Sx,Sz)-5.76*f0^2*(1-16*(0.6*f0*time-1)^2)*exp(-8*(0.6*f0*time-1)^2);
%Uprev=Unow; %波场更新
Unow=Unext;
Vnow=Vnext;
%Vprev=Vnow; %波场更新
Rnow=Rnext;
%Pprev=Pnow; %波场更新
Hnow=Hnext;
Tnow=Tnext;
end
% max(max(Vnext))
%绘图
surf(Rnow)
shading interp;
fip=fopen('D:\mitchelles\Fimage\elsU1_SD.bin','wb');
fwrite(fip,Unow,'float');
fclose(fip);
fip=fopen('D:\mitchelles\Fimage\elsV1_SD.bin','wb');
fwrite(fip,Vnow,'float');
fclose(fip);
fip=fopen('D:\mitchelles\Fimage\elsH1_SD.bin','wb');
fwrite(fip,Hnow,'float');
fclose(fip);
fip=fopen('D:\mitchelles\Fimage\elsT1_SD.bin','wb');
fwrite(fip,Tnow,'float');
fclose(fip);
fip=fopen('D:\mitchelles\Fimage\elsR1_SD.bin','wb');
fwrite(fip,Rnow,'float');
fclose(fip);
view(2);%view(90,90)
colormap(gray);
toc
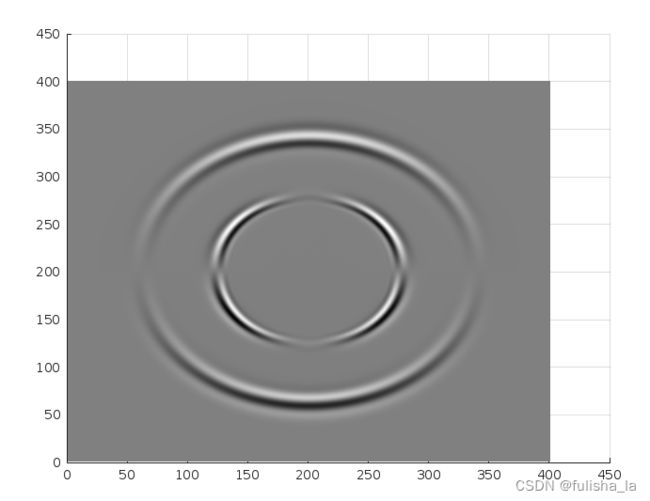
matlab代码-(对应他离散化的格式):下面是复杂的弹性波格式
% 主程序
for time=0:delta_t:Endtime
for i=7:CNX-6
for j=7:CNZ-6
%X1 = Rnow(i+1,j) - Rnow(i,j);
X1 = c1*(Rnow(i+1,j) - Rnow(i,j)) + c2*(Rnow(i+2,j) - Rnow(i-1,j)) + c3*(Rnow(i+3,j) - Rnow(i-2,j)) + c4*(Rnow(i+4,j) - Rnow(i-3,j))+ c5*(Rnow(i+5,j) - Rnow(i-4,j))+ c6*(Rnow(i+6,j) - Rnow(i-5,j));
%Y1x = Hnow(i,j) - Hnow(i,j-1);
Y1x = c1*(Hnow(i,j) - Hnow(i,j-1))+c2*(Hnow(i,j+1) - Hnow(i,j-2))+c3*(Hnow(i,j+2) - Hnow(i,j-3))+c4*(Hnow(i,j+3) - Hnow(i,j-4))+c5*(Hnow(i,j+4) - Hnow(i,j-5))+c6*(Hnow(i,j+5) - Hnow(i,j-6));
%Y1z = Hnow(i,j) - Hnow(i-1,j);
Y1z = c1*(Hnow(i,j) - Hnow(i-1,j))+c2*(Hnow(i+1,j) - Hnow(i-2,j))+c3*(Hnow(i+2,j) - Hnow(i-3,j))+c4*(Hnow(i+3,j) - Hnow(i-4,j))+c5*(Hnow(i+4,j) - Hnow(i-5,j))+c6*(Hnow(i+5,j) - Hnow(i-6,j));
%Z1 = Tnow(i,j+1) - Tnow(i,j);
Z1 = c1*(Tnow(i,j+1) - Tnow(i,j))+c2*(Tnow(i,j+2) - Tnow(i,j-1))+c3*(Tnow(i,j+3) - Tnow(i,j-2))+c4*(Tnow(i,j+4) - Tnow(i,j-3))+c5*(Tnow(i,j+5) - Tnow(i,j-4))+c6*(Tnow(i,j+6) - Tnow(i,j-5));
delta_u = (X1+Y1x)*delta_t/(Urho(i,j)*delta_x);
Unext(i,j)=Unow(i,j) + delta_u;
delta_v = (Y1z+Z1)*delta_t/(Vrho(i,j)*delta_z);
Vnext(i,j)=Vnow(i,j) + delta_v;
end
end
for i=7:CNX-6
for j=7:CNZ-6
%M1 = Unext(i,j) - Unext(i-1,j);
M1 = c1*(Unext(i,j) - Unext(i-1,j))+c2*(Unext(i+1,j) - Unext(i-2,j))+c3*(Unext(i+2,j) - Unext(i-3,j))+c4*(Unext(i+3,j) - Unext(i-4,j))+c5*(Unext(i+4,j) - Unext(i-5,j))+c6*(Unext(i+5,j) - Unext(i-6,j));
%Mn1 = Unext(i,j+1) - Unext(i,j);
Mn1 = c1*(Unext(i,j+1) - Unext(i,j))+c2*(Unext(i,j+2) - Unext(i,j-1))+c3*(Unext(i,j+3) - Unext(i,j-2))+c4*(Unext(i,j+3) - Unext(i,j-4))+c5*(Unext(i,j+4) - Unext(i,j-5))+c6*(Unext(i,j+5) - Unext(i,j-6));
%N1 = Vnext(i,j) - Vnext(i,j-1);
N1 = c1*(Vnext(i,j) - Vnext(i,j-1))+c2*(Vnext(i,j+1) - Vnext(i,j-2))+c3*(Vnext(i,j+2) - Vnext(i,j-3))+c4*(Vnext(i,j+3) - Vnext(i,j-4))+c5*(Vnext(i,j+4) - Vnext(i,j-5))+c6*(Vnext(i,j+5) - Vnext(i,j-6));
%Nm1 = Vnext(i+1,j) - Vnext(i,j);
Nm1 = c1*(Vnext(i+1,j) - Vnext(i,j))+c2*(Vnext(i+2,j) - Vnext(i-1,j))+c3*(Vnext(i+3,j) - Vnext(i-2,j))+c4*(Vnext(i+4,j) - Vnext(i-3,j))+c5*(Vnext(i+5,j) - Vnext(i-4,j))+c6*(Vnext(i+6,j) - Vnext(i-5,j));
delta_r = delta_t*(RTc11(i,j)*M1+RTc13(i,j)*N1)/delta_x;
Rnext(i,j) = Rnow(i,j) + delta_r;
delta_tn = delta_t*(RTc13(i,j)*M1+RTc33(i,j)*N1)/delta_x;
Tnext(i,j) = Tnow(i,j) + delta_tn;
delta_h = delta_t*(Hc44(i,j)*Mn1+Hc44(i,j)*Nm1)/delta_x;
Hnext(i,j) = Hnow(i,j) + delta_h;
end
end
Unext(Sx,Sz)=Unext(Sx,Sz)-5.76*f0^2*(1-16*(0.6*f0*time-1)^2)*exp(-8*(0.6*f0*time-1)^2);
for m = 1:CNX
Fnow(nk,m) = Unow(Sx,m);
Anow(nk,m) = Unow(m,Sz);
end
%Uprev=Unow; %波场更新
Unow=Unext;
Vnow=Vnext;
%Vprev=Vnow; %波场更新
Rnow=Rnext;
%Pprev=Pnow; %波场更新
Hnow=Hnext;
Tnow=Tnext;
nk = nk+1;
end