热门二叉树面试题
606. 根据二叉树创建字符串 - 力扣(LeetCode)
给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。
空节点使用一对空括号对 "()" 表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1:
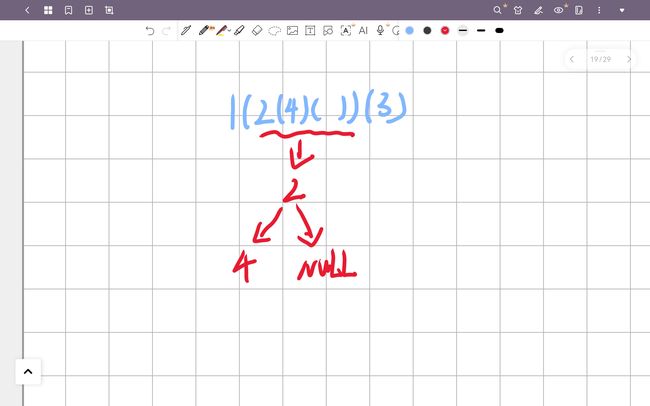
输入:root = [1,2,3,4]
输出:"1(2(4))(3)"
解释:初步转化后得到 "1(2(4)())(3()())" ,但省略所有不必要的空括号对后,字符串应该是"1(2(4))(3)" 。
示例 2:
输入:root = [1,2,3,null,4]
输出:"1(2()(4))(3)"
解释:和第一个示例类似,但是无法省略第一个空括号对,否则会破坏输入与输出一一映射的关系。
分析:示例一当中输入1,2,3,4,然后输出1,2,4,3。那么已经很容易看出来是一个二叉树前序遍历了,二叉树的前序遍历顺序为中 左 右,解决了顺序问题,接下来就是括号的问题了。
一共有四种情况
1:只有左儿子
2:只有右儿子
3:没有左右儿子
4:有左右儿子
然后化简之后可以得到
1(2(4))(3)。
class Solution {
public:
void Pre(TreeNode* t,string& str)
{
if(t==nullptr) return;//为空直接返回,包括了没有左右儿子的情况,直接不打印
str+=to_string(t->val);
if(t->left)//左子树
{
str+="(";
Pre(t->left,str);
str+=")";
}
if(t->right)//右子树
{
str+="(";
Pre(t->right,str);
str+=")";
}
}
string tree2str(TreeNode* root) {
string res="";
Pre(root,res);
return res;
}
};
但是和结果好像不一样,少了一个括号,我们来模拟一下。
当递归到节点2的时候,2->left为空,就直接返回了,返回了之后就会导致这里没有打印任何东西,所以导致结果出错,因此第一个if条件可以改为if(t->left||t->right)。
class Solution {
public:
void Pre(TreeNode* t,string& str)
{
if(t==nullptr) return;//为空直接返回,包括了没有左右儿子的情况,直接不打印
str+=to_string(t->val);
if(t->left||t->right)//左子树/左子树和右子树都存在
{
str+="(";
Pre(t->left,str);
str+=")";
}
if(t->right)//右子树
{
str+="(";
Pre(t->right,str);
str+=")";
}
}
string tree2str(TreeNode* root) {
string res="";
Pre(root,res);
return res;
}
};
102. 二叉树的层序遍历 - 力扣(LeetCode)
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
层序遍历,BFS,老套路题了,用一个队列来模拟遍历的过程。
比如一开始3入队,拿到节点3,3出队,然后把3还有3的左右子节点加入答案,把9和20加入队列,然后拿到节点9,出队,9没有左右子节点,所以继续拿到节点20,20再出队,把20和20的左右子节点都加入答案即可。
class Solution {
public:
vector> levelOrder(TreeNode* root) {
vector>res;
if(!root) return res;
queueq;
q.push(root);
while(!q.empty())
{
vectortmp;
int sz=q.size();//记录当前层数有多少节点,就要循环取多少次,一定要提前记录,不然q.size()会改变。
for(int i=0;ival);//入暂存的答案数组
q.pop();//出队
if(node->left)
{
q.push(node->left);
}
if(node->right)
{
q.push(node->right);
}
}
res.push_back(tmp);
}
return res;
}
};
107. 二叉树的层序遍历 II - 力扣(LeetCode)
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
这题没什么说的,在上一题的基础上对结果进行逆置就好了。
class Solution {
public:
vector> levelOrderBottom(TreeNode* root) {
queueq;
if(root!=nullptr)
{
q.push(root);
}
vector>res;
while(!q.empty())
{
int size=q.size();
vector vec;
for(int i=0;ival);
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
res.push_back(vec);
}
reverse(res.begin(),res.end());
return res;
}
};
236. 二叉树的最近公共祖先 - 力扣(LeetCode)
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
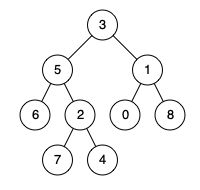
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
这道题一共有三种情况。
1:都在左子树
2:都在右子树
3:一个在左,一个在右
首先看最好判断的一个在左一个在右的情况这种情况的最近公共祖先就是根节点。
然后是在左子树的:我们只需要在左子树搜索第一个找到
p或者q的那个节点就是最近公共祖先。右子树和左子树同理。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==nullptr||root==p||root==q) return root;
TreeNode* left=lowestCommonAncestor(root->left,p,q);
TreeNode* right=lowestCommonAncestor(root->right,p,q);
if(left==nullptr) return right;
else if(right==nullptr) return left;
return root;
}
};
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
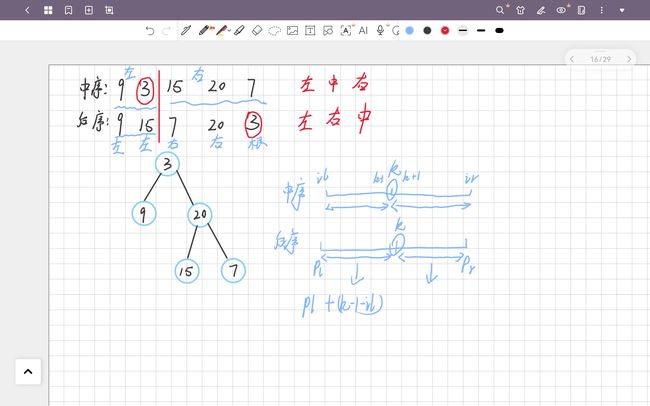
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
前序遍历顺序:中 左 右
中序遍历顺序:左 中 右
可以看出来,前序遍历的第一个节点就是根节点,找到根节点就可以利用中序遍历来确定左右子树的个数
比如下图,前序遍历的第一个节点是3,那么根节点就是3,再去中序遍历找3,以3为界限划分左右子树,9就是左边的,20,15,7算是右边的。
class Solution {
public:
unordered_mappos;
TreeNode* buildTree(vector& preorder, vector& inorder) {
for(int i=0;i& preorder,vector& inorder,int pl,int pr,int il,int ir)
{
if(pl>pr) return nullptr;
TreeNode* root=new TreeNode(preorder[pl]);//前序遍历的第一个元素是根节点
int pos1=pos[root->val];
root->left=build(preorder,inorder,pl+1,pl+1+pos1-1-il,il,pos1-1);
root->right=build(preorder,inorder,pl+1+pos1-il,pr,pos1+1,ir);
return root;
}
};
106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
思路和上题几乎一样,分析如上图
class Solution {
public:
unordered_mappos;
TreeNode* buildTree(vector& inorder, vector& postorder) {
for(int i=0;i& inorder,vector&postorder,int il,int ir,int pl,int pr)
{
if(pl>pr)return nullptr;
TreeNode* root=new TreeNode(postorder[pr]);
int k=pos[root->val];
root->left=build(inorder,postorder,il,k-1,pl,pl+(k-1-il));
root->right=build(inorder,postorder,k+1,ir,pl+k-il,pr-1);
return root;
}
};
144. 二叉树的前序遍历 - 力扣(LeetCode)
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
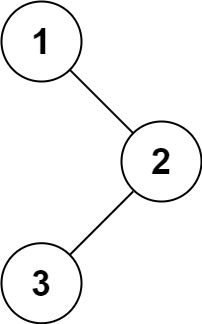
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
输入:root = [1,2]
输出:[1,2]
示例 5:
输入:root = [1,null,2]
输出:[1,2]
前序遍历递归版本很简单:
class Solution {
public:
vectorres;
vector preorderTraversal(TreeNode* root) {
pre(root);
return res;
}
void pre(TreeNode* root)
{
if(root==nullptr)return;
res.push_back(root->val);
pre(root->left);
pre(root->right);
}
};
非递归版本:
前序遍历为:中 左 右,所以先一直往节点的左节点走,然后再走右边,边走边将当前节点的值加入答案当中即可。
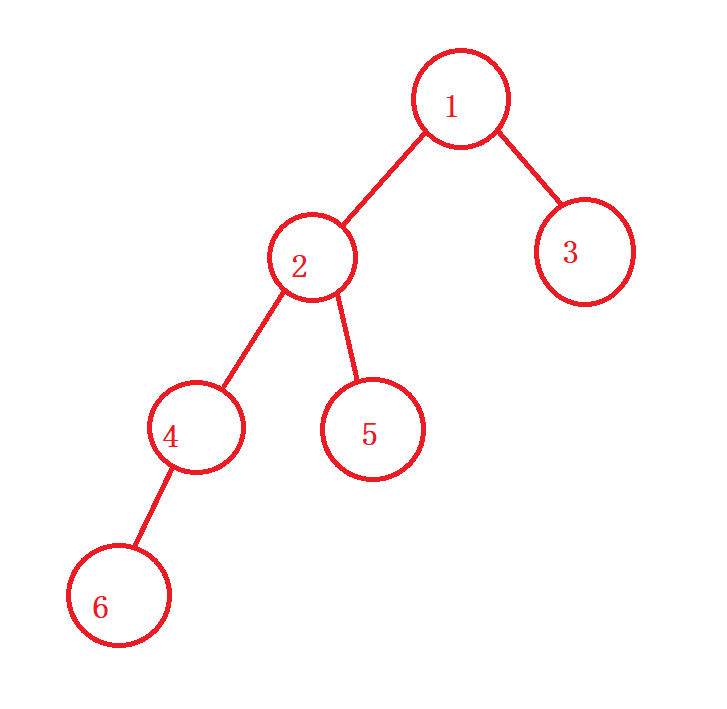
这里可以用一个栈来模拟一下过程,假如是这样一棵树
一直循环走左节点
1 2 4 6,并且将其加入栈和答案,如果没有右节点就会一直pop栈内的元素,一直到节点2,2存在右节点,就将5加入栈和答案,5没有右节点,就会继续出栈,一直出到1,节点1存在右节点,就讲3又加入栈和答案,最后pop,然后返回答案即可。
class Solution {
public:
vector preorderTraversal(TreeNode* root) {
vector res;
if (root == nullptr) {
return res;
}
stack st;
TreeNode* node = root;
while(node!=nullptr||!st.empty())
{
while(node!=nullptr)
{
//遍历左子树
st.push(node);
res.push_back(node->val);
node=node->left;
}
//遍历了左子树,就要取节点然后遍历右子树了
node=st.top();
st.pop();
node=node->right;
}
return res;
}
};
94. 二叉树的中序遍历 - 力扣(LeetCode)
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
递归版本:
class Solution {
public:
vectorres;
vector inorderTraversal(TreeNode* root) {
inorder(root);
return res;
}
void inorder(TreeNode* root)
{
if(root==nullptr) return;
inorder(root->left);
res.push_back(root->val);
inorder(root->right);
}
};
非递归版本:
同样对于如图的一棵树
中序遍历:左 中 右
6 4 2 5 1 3是中序遍历的答案。中序遍历和前序遍历的非递归方式不同点在于,不能在路循环走左子树的时候一并把结点的值加入答案,只能加入栈当中。等到走完了左子树才能够将当前节点加入到答案当中,然后继续取栈中的节点,然后pop栈中的节点,再去走右节点。
class Solution {
public:
vectorres;
stack st;
vector inorderTraversal(TreeNode* root) {
if(root==nullptr) return res;
TreeNode* node=root;
while(node!=nullptr||!st.empty())
{
while(node!=nullptr)
{
st.push(node);
node=node->left;
}
node=st.top();
st.pop();
res.push_back(node->val);
node=node->right;
}
return res;
}
};
145. 二叉树的后序遍历 - 力扣(LeetCode)
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
输入:root = [1,null,2,3]
输出:[3,2,1]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
直接给非递归版本吧
这里最需要注意的一点就是避免重复将一个节点加入答案当中最后造成死循环。
和前序、中序遍历一样,先走完左子树,然后判断右子树,假如我只判断右子树是否为空,在走到节点7回到节点2的时候,这时候要去走2->right,很明显,2->right存在,所以4会被加入答案和栈当中,这时候将节点node置为nullptr,就能避开继续走左子树,直接取栈顶的节点4,4没有右子树了,所以节点4又会被加入到栈当中,就会造成死循环。
在这里可以利用一个pre节点来保存上一次加入栈当中的节点,然后判断是否和pre重复。
class Solution {
public:
vector postorderTraversal(TreeNode *root) {
vector res;
if (root == nullptr) {
return res;
}
stack st;//stack
TreeNode* node=root;//当前节点
TreeNode *prev = nullptr;//上一次加入答案的节点
while(node!=nullptr||!st.empty())
{
//递归完左区间
while(node!=nullptr)
{
st.push(node);
node=node->left;
}
node=st.top();//取栈顶
st.pop();//出栈
//判断是否有右子树
if(node->right==nullptr||node->right==prev)
{
res.push_back(node->val);
prev=node;//记录每一次加入答案的点,防止重复加入死循环
node=nullptr;
}else
{
//如果还有右边的节点,就重写把根节点入栈,然后让root指向右节点,让右节点加入答案
st.push(node);
node=node->right;
}
}
return res;
}
};