LeetCode-200-岛屿数量
题意描述:
给定一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
示例:
示例一:
输入:
11110
11010
11000
00000
输出: 1
示例二:
输入:
11000
11000
00100
00011
输出: 3
解题思路:
Alice: 怎么判断不同的“1”是不是同一个岛屿呢 ?
Bob:看题目里面的定义,相邻而且必须是横向后者纵向上直接相邻,只要是相邻的一块“1”或者一个“1”就能构成一个岛屿?
Alice: 也就是说,如果是对角线相邻的话,是不能算成一个岛屿的?
Bob: 对,不过判断不同的“1”是不是同一个岛屿可能不是一个好的思路,我好像做过类似的题目,是用宽度优先搜索或者深度优先搜索的方法做的。
Alice: 搜索 ?就是遍历整个二维数组吗 ?
Bob: 也算是一种遍历,不过遍历的方法不一样。宽度优先搜索是优先搜索自己身边的元素,深度优先搜索是尽量先一条道走到黑。我还是画个图比较好理解一些。
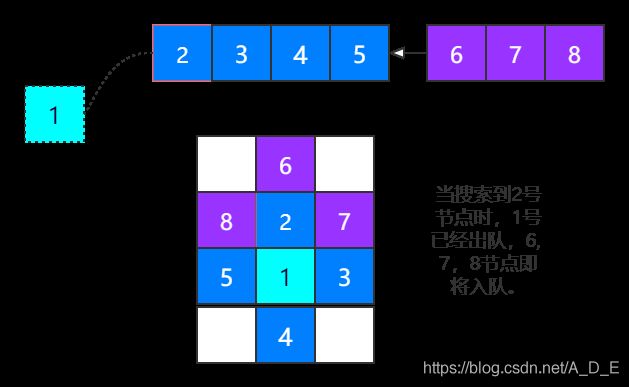

Alice: 上面是宽度优先搜索,下面是深度优先搜索 ? 大概能理解了。那这道题应该就是二重循环遍历整个数组,如果找到一个“1”,就用DFS或者BFS找到这个小岛的其余部分,然后打上标记,就不会重复计算小岛的数目了。
Bob: 没错,我们只记录第一次找到的那个“1”,其余的用DFS或者BFS找到就可以了,打标记可以直接打在输入的二维数组里面,反正也是参数,用DFS或者BFS找到的直接修改成"0"就好了,这样还可以省内存。
Alice: 不错不错。
代码:
Python 方法一: BFS,队列 + 循环。
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
if len(grid) == 0:
return 0
self.matrix = []
for x in range(len(grid)):
tmp = []
for z in range(len(grid[0])):
tmp.append(int(grid[x][z]))
self.matrix.append(tmp)
self.rows = len(self.matrix)
self.clos = len(self.matrix[0])
# print(self.rows)
# print(self.clos)
# print(self.matrix)
cnt = 0
for x in range(len(self.matrix)):
for z in range(len(self.matrix[0])):
if self.matrix[x][z] == 1:
cnt += 1
self.matrix[x][z] = 0
self.clear(x,z)
#print(self.matrix)
return cnt
def clear(self, x, z):
directions = [[0,1],[0,-1],[-1,0],[1,0]]
dots = [[x, z]]
while len(dots) > 0:
tmp = dots.pop(0)
xx = tmp[0]
zz = tmp[1]
for direction in directions:
tmpx = xx + direction[0]
tmpz = zz + direction[1]
if tmpx >= 0 and tmpx < self.rows and tmpz >= 0 and tmpz < self.clos:
if self.matrix[tmpx][tmpz] == 1:
#print("test")
dots.append([tmpx, tmpz])
self.matrix[tmpx][tmpz] = 0
return
Java 方法一: BFS,ArrayList作为 队列 + 循环。
class Solution {
public int numIslands(char[][] grid) {
if(grid.length == 0){
return 0;
}
int cnt = 0;
int rows = grid.length;
int clos = grid[0].length;
int[][] directions = {{0,1},{0,-1},{1,0},{-1,0}};
for(int i=0; i<grid.length; ++i){
for(int j=0; j<grid[i].length; ++j){
if(grid[i][j] == '1'){
cnt += 1;
grid[i][j] = 'x';
ArrayList<ArrayList<Integer>> dots = new ArrayList();
ArrayList<Integer> tmp = new ArrayList();
tmp.add(i);
tmp.add(j);
dots.add(tmp);
while(dots.isEmpty() == false){
int x = dots.get(0).get(0);
int y = dots.get(0).get(1);
dots.remove(0);
for(int[] direciton : directions){
int xx = x + direciton[0];
int yy = y + direciton[1];
if(xx >= 0 && xx < rows && yy >= 0 && yy < clos && grid[xx][yy] == '1'){
ArrayList<Integer> anotherTmp = new ArrayList();
anotherTmp.add(xx);
anotherTmp.add(yy);
dots.add(anotherTmp);
grid[xx][yy] = 'x';
}
}
}
}
}
}
return cnt;
}
}
Python 方法二: DFS, 深度优先循环,递归。
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
cnt = 0
for x in range(len(grid)):
for y in range(len(grid[0])):
if grid[x][y] == '1':
cnt += 1
self.dfs(grid, x, y)
# 清除与该点相邻的其他点
return cnt
def dfs(self, grid, x, y):
if x >= 0 and x < len(grid) and y >=0 and y < len(grid[x]) and grid[x][y] == '1':
grid[x][y] = '0'
self.dfs(grid, x-1, y)
self.dfs(grid, x+1, y)
self.dfs(grid, x, y+1)
self.dfs(grid, x, y-1)
Java 方法二: DFS, 递归实现深度优先搜索,反而快了不少。
class Solution {
public int numIslands(char[][] grid) {
int cnt = 0;
for(int i=0; i<grid.length; ++i){
for(int j=0; j<grid[i].length; ++j){
if(grid[i][j] == '1'){
cnt ++;
dfs(grid, i, j);
}
}
}
return cnt;
}
public void dfs(char[][] grid, int x, int y){
if(x >= 0 && x < grid.length && y >= 0 &&y < grid[x].length && grid[x][y] == '1'){
grid[x][y] = '0';
dfs(grid, x+1, y);
dfs(grid, x-1, y);
dfs(grid, x, y+1);
dfs(grid, x, y-1);
}
return;
}
}
易错点:
- 一些测试点:
[]
[[]]
[["1","1","1"]]
[["1","1","1"],["1","1","1"],["1","1","1"]]
[["1","1","1"],["1","0","1"],["1","1","1"]]
[["1","0","1"],["0","0","0"],["1","0","1"]]
[["1","0","1"],["0","1","0"],["1","0","1"]]
[["1","1","1","1","0"],["1","1","0","1","0"],["1","1","0","0","0"],["0","0","0","0","0"]]
- 答案:
0
0
1
1
1
4
5
1
总结:
- DFS要靠递归,BFS要靠队列。