流量矩阵常见的两种估计方法对比

一、补充线性代数知识：

1.线性方程组：

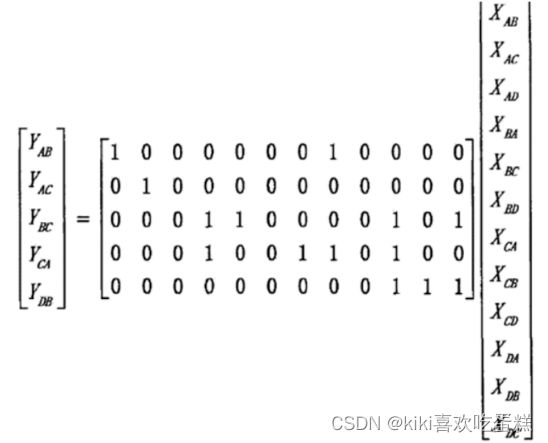
拿求解流量矩阵的方程来讲：
$$Y=AX$$
原因：OD对的数目是远比实际链路的数目要多，未知数的个数远比方程组的个数要多。

线性方程组的解个数与秩的关系：

对线性方程组，其解的数量可以根据A的秩来讨论。A ∈ R （m × n） 。
$$AX=Y$$

1. r = m< n , 即矩阵A行满秩，此时A有m个线性无关的列，也就是说其列空间为R m ，此时对任意Y方程组均有解，同时Ax = 0 一定有非零解，方程组有无穷多解。
2. r = n < m ，即矩阵A列满秩，此时A有n个线性无关的列，方程组Ax = 0 只有零解，方程组有0或1个解（取决于b）。
3. r < m , n ，即矩阵A行列均不满秩，A x = 0 一定有非零解，则Ax = Y有0 或无穷多个解。
4. r = m = n，矩阵A是可逆方阵，此时A x = 0 只有零解，并且A的列空间为R m，方程组有一个解。
   

二、万有引力定律为何可以推广到重力模型？

• 在牛顿的地球重力定律中，自然界中任何两个质点都以一定的力互相吸引着，这个力同两个质点的质量乘积m1 * m2成正比，同它们之间的距离 R 的平方成反比。
• 类比万有引力定律公式：

1. Xij代表了矩阵元素中 i 到 j 的力，
2. Ri 代表了和**“离开”i** 相联系的排斥因素，
3. Aj 代表了和“去向”j 相联系的吸引因素，
4. fij 代表了从 i 到 j 的摩擦因素。

• 在流量矩阵估算研究中，通常把 Xij 解释为从 i 点进入网络，从 j 点离开网络的流量；把排斥因素Ri 解释为从 i 点进入网络的流量；把吸引因素Aj 解释为从 j 点离开网络的业务流量；摩擦因素fij 根据不同的源/目的节点对而有不同的定义。

三、重力模型合不合理？在哪些时候合理？

1.简单重力模型：

• 在大型IP骨干网络中，应该考虑到更多的链路分类信息和路由策略信息来对ISP的OD流量建模，由于网络边缘链路的分类不同，实际网络流量流经不同边缘链路的路由策略是不同的，通用重力模型建立在对OD流量条件独立的假设上。
• 摩擦因子是针对不同 OD 对的位置信息；由于对于摩擦因子矩阵中每个元素进行推断是很复杂的，从而简化将摩擦因子看为常量。
• 节点对间的 OD 流量对于流量的组成细节很敏感，这里简单重力模型对 IP 骨干网络边缘链路 OD 流对进行估计，在简单重力模型中对网络边缘链路不做区分，这种模糊的处理会为模型的精度引入误差。

2.通用重力模型：

• 相较于简单重力模型改进：结合了实际网络的路由策略，区分边缘接入链路种类和 OD 流种类，对每类 OD 流分别估计，重力模型的 估计精度得到了提高。
• 重力模型得到初始解一般不满足 IP 骨干网内部层析成像方程的约束。

四、论文图表复现

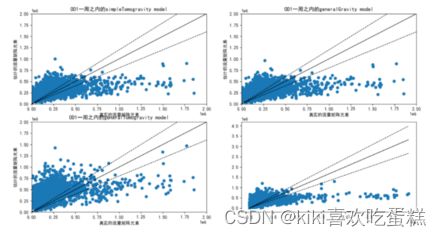
1.选取OD_1画图，将四个估计模型放在一起对比1

2.分开画图：

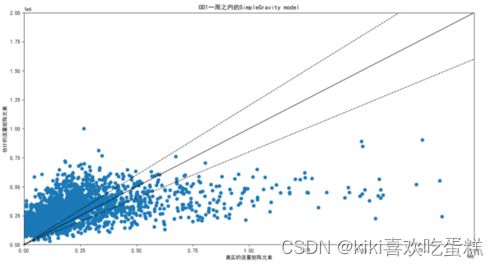
（1）simpleGravity

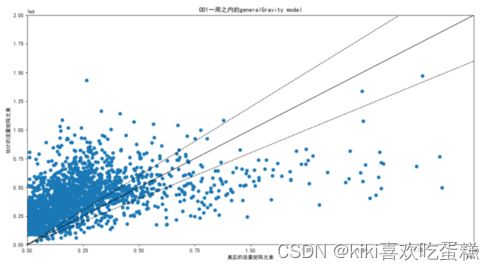
（2）generalGravity

对于 Abilene，simpleGravity 和 generalGravity 给出了相似的结果。但在其他网络中，generalTomogravity 往往表现得非常好。

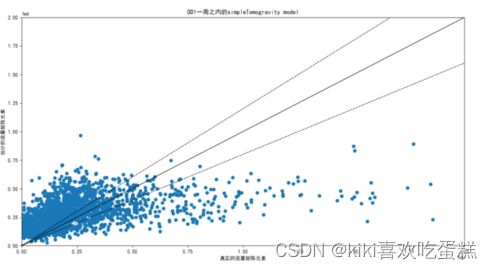
（3）simpleTomogravity

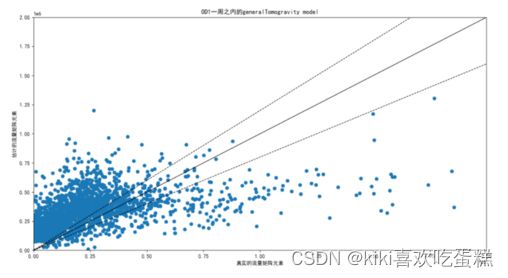
（4）generalTomogravity

3.相关系数分布图：

知识补充:累积分布函数CDF

累积分布函数 (CDF) 计算给定 x 值的累积概率。可使用 CDF 确定取自总体的随机观测值将小于或等于特定值的概率。还可以使用此信息来确定观测值将大于特定值或介于两个值之间的概率。

关键代码如下：

# =============绘制simpleGravity-cdf图===============
ecdf = sm.distributions.ECDF(pccs_sG)
# 等差数列，用于绘制X轴数据
x1 = np.linspace(min(pccs_sG), max(pccs_sG))
# x轴数据上值对应的累计密度概率
y1 = ecdf(x1)

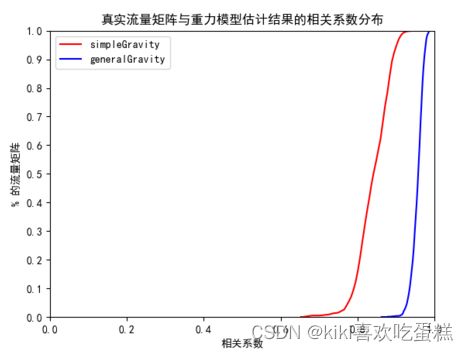
可以看出通用重力模型效果优于简单重力模型，相关系数更接近1。
寻找SG与GG相关系数的上下限（X02文件）：
通过计算144个OD对在一周时间内的总流量值（每5分钟采样）可以看出，SG与GG的上限值对应的OD流为大流量OD，下限值对应的OD为小流量OD。可以得出结论：当OD流较大时，generalizedgravi与simplegravi模型估计较为准确。

五.计算分析：

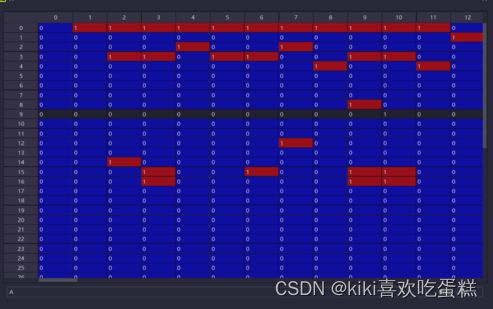
1.确定路由矩阵：

首先分析links文件：

有30条链路为内部链路，12条为入站，12条为出站。

有12个节点。

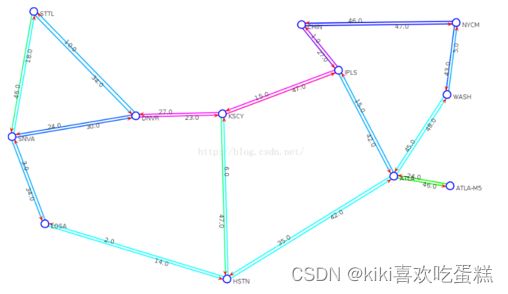
图片来自：https://blog.csdn.net/canhui_wang/article/details/51322916
分析A文件：

link(x,y)：链路对应links文件中的编号（1-54）
dmd(s,d)：为OD对的路由路径，编号1-144（因为有12个节点，12✖12=144）

综上两个文件，可以得出路由矩阵为54✖144=7776。

如图所示通过python做出路由矩阵：

2.反解链路流量Y

由路由矩阵A（54✖144）和真实OD_1(144✖1)做矩阵乘法可以解出链路流量Y（54✖1）。

求得链路流量Y（54✖1）如下图所示：

3.实现对simplegravity重新计算，验证idea：

我们选择一个边缘节点：ATLA-M5进行分析（入站出站为同一节点）。
在links文件中找到对应编号：
有30条链路为内部链路，12条为入站，12条为出站。入站总流量与出站总流量应该是相等：
经验证计算正确：

T_ATLAM5=(Y[30]*Y[31])/Y_inbound # 与Y_outbound完全等价

五个流量矩阵的排列顺序依次为：
， ， ， ， …

4.运用自己计算的simplegravity结果重新画图、

寻找规律，可以看出数组下标对应关系如下：

# Y[30] * Y[31]--simpleGravity_OD[0]
# Y[30] * Y[33]--simpleGravity_OD[1]
# Y[30] * Y[35]--simpleGravity_OD[2]
# Y[30] * Y[37]--simpleGravity_OD[3]
# Y[30] * Y[39]--simpleGravity_OD[4]
# Y[30] * Y[41]--simpleGravity_OD[5]
# Y[30] * Y[43]--simpleGravity_OD[6]
# Y[30] * Y[45]--simpleGravity_OD[7]
# Y[30] * Y[47]--simpleGravity_OD[8]
# Y[30] * Y[49]--simpleGravity_OD[9]
# Y[30] * Y[51]--simpleGravity_OD[10]
# Y[30] * Y[53]--simpleGravity_OD[11]
# Y[32] * Y[31]--simpleGravity_OD[12]
# Y[32] * Y[33]--simpleGravity_OD[13]
# Y[32] * Y[35]--simpleGravity_OD[14]
# Y[32] * Y[37]--simpleGravity_OD[15]
# Y[32] * Y[39]--simpleGravity_OD[16]
# Y[32] * Y[41]--simpleGravity_OD[17]
# Y[32] * Y[43]--simpleGravity_OD[18]
# Y[32] * Y[45]--simpleGravity_OD[19]
# Y[32] * Y[47]--simpleGravity_OD[20]
# Y[32] * Y[49]--simpleGravity_OD[21]
# Y[32] * Y[51]--simpleGravity_OD[22]
# Y[32] * Y[53]--simpleGravity_OD[23]

核心算法如下：

# 计算simplegravity模型估计出的流量矩阵：T_sG (时间为一周）
T_sG = np.zeros((2016,144), dtype=float)
S= (Y[0][30] * Y[0][31]) / Y_inbound[0]
for p in range(0,2016):
    k = 31
    t = 30
    j = 0
    for count in range(0, 12):
        for i in range(0, 12):
            T_sG[p][j] = (Y[p][t] * Y[p][k]) / Y_inbound[p]  # 与Y_outbound完全等价
            j = j + 1
            if k < 54:
                k = k + 2
        if t < 54:
            t = t + 2
        k = 31

通过计算得出T_sG并重新作图：

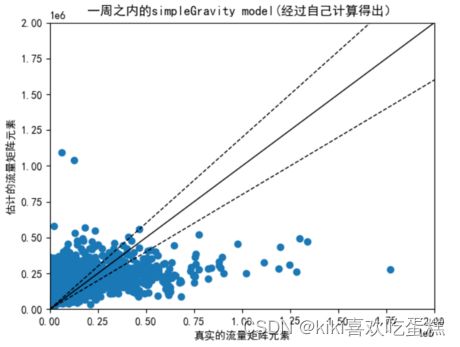
将realOD换位数据给出的SG结果作图：

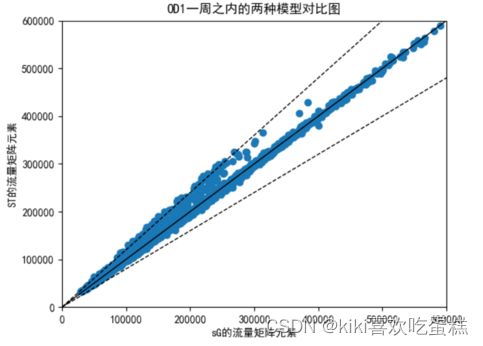
通过作图可以看出小流量OD的误差很大，离开了+/-20%的区域。

5.计算简单重力模型的rmse：

使用sklearn库中的mean_squared_error求出mse再开方，最后换算单位为Mbps（兆比特每秒）

6.绘制简单重力模型估计最好OD与最差OD流量图：

通过求解24周所有OD的rmse来判断最好OD与最差OD：
rmse是一个1×144的数组：
通过求解可知，最好OD为第10条，最差OD为第32条。
分别画出他们一周流量图：
真实OD作图：

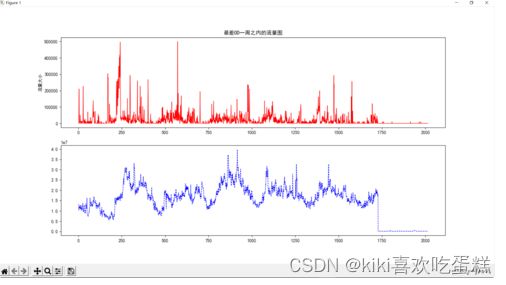
simplegravity模型数据作图：

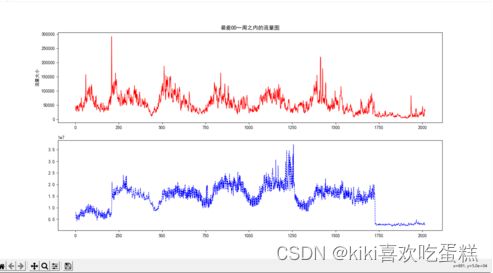
知识补充：潮汐效应（tidal effect）

在通信系统中“潮汐效应”是指工作时间人们在CBD区域大量聚集，下班后又向居民区大量迁徙的现象。这种现象引发了移动通信系统中话务量的流动，使得热点区域在特定时刻出现突发大话务量，导致网络拥塞、无法接入；对于建网初期的容量规划也带来一定的困难。而在应对该类型区域内大话务量流动的同时，实现降低建网成本，提升运营核心竞争力，成为摆在运营商面前的一道棘手难题。
从上图看，上面两条OD在周末时流量几乎为0，存在潮汐效应，下面我们找出144条OD中存在潮汐效应的OD。
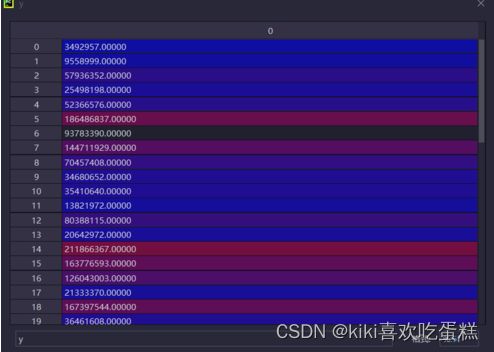
144条OD流量的表格：

我们选取的日期段为 2004-03-08 (X02):

一周内流量之和最大的OD为第144条，流量最小OD为第109条：

寻找存在潮汐效应的OD：

我们通过观察每个OD周六日两天的流量的情况来判断OD是否存在潮汐效应，选取real_OD数组中第1440-2016行，有很多存在流量为0的OD则认为其存在潮汐效应。（我们假设出现流量为0的次数大于100的OD为存在潮汐效应）

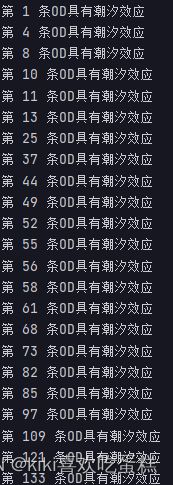
画出部分OD的一周流量图可以发现确实存在潮汐效应。

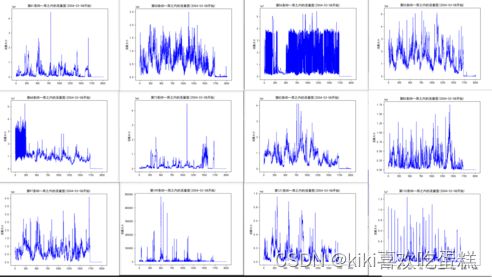
7.simplegravity算法适用情况

模型估计结果最好的OD为第10个OD，最差为第32个OD，从文件A中找到：

link(x,y) dmd(s,d) link_index dmd_index frac
*,ATLA-M5 ATLA-M5,SNVAng 31 10 1  #最好OD
*,CHINng CHINng,LOSAng 35 32 1    #最差OD

算法好的时候，数据应该是附和万有引力模型的，从论文中的图6的累计分布函数中simplegravity对应的上下限可以得出结论：当OD流较大时，简单重力模型估计效果较好。

github仓库链接