栈和队列OJ——循环队列设计,括号栈匹配问题
文章目录
-
- @[toc]
- ⭐循环队列
-
-
- 循环队列顺序表
-
- 循环队列入队
- 循环队列出队
- 取队头和队尾数据
- 循环队列释放
-
- 题目小练
- ⭐括号匹配
-
-
- 括号栈匹配算法
- ⭐后话
文章目录
-
- @[toc]
- ⭐循环队列
-
-
- 循环队列顺序表
-
- 循环队列入队
- 循环队列出队
- 取队头和队尾数据
- 循环队列释放
-
- 题目小练
-
- ⭐括号匹配
-
-
- 括号栈匹配算法
-
- ⭐后话
⭐循环队列
循环队列是一种特殊的线性结构,其以数据的先进先出FIFO性作为最大特征,在前面章节的论述中,我们以单链表为基本结构实现了队列(详情请参考该博客:数据结构——栈和队列_VelvetShiki_Not_VS的博客-CSDN博客)。对于循环队列的设计而言,因为需要实现数据的首尾相连,单链表可以是一种实现方式。本章中采用顺序表的循环队列实现方式,考虑到普通队列以连续的顺序表空间只能不断向后使用内存存储数据,但是却无法使用之前使用过的内存空间来重复利用空间,循环队列的顺序表实现正是考虑到这一点,所以循环队列的顺序表实现对内存空间的利用率很高,既能使数据满足先进先出的特性,同时又可以满足数据只能尾插,头删等队列的基本特点,是一个较好的数据存储模式。
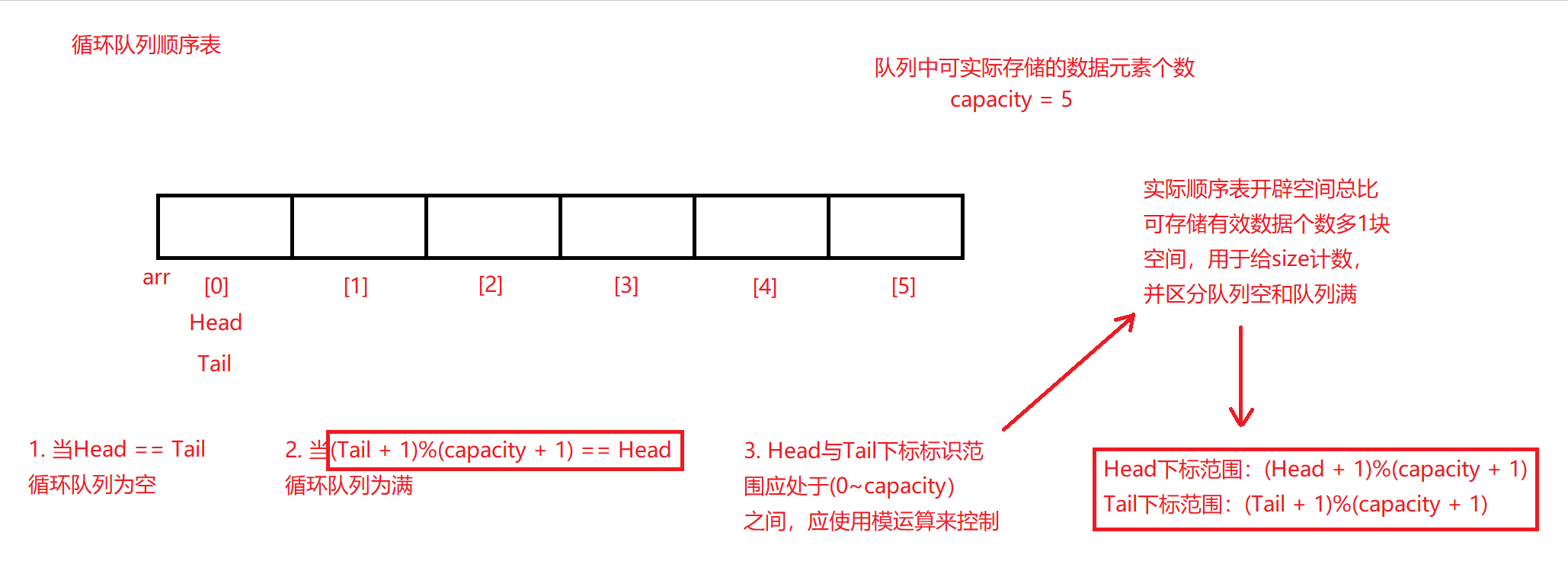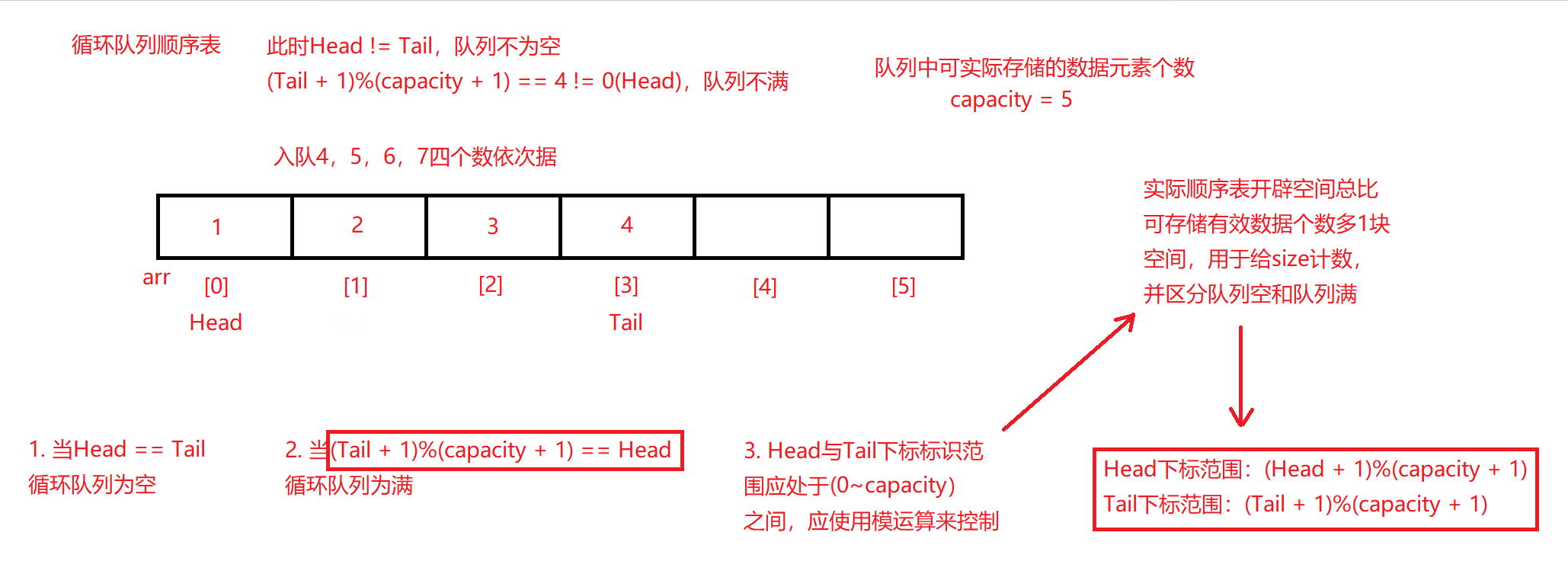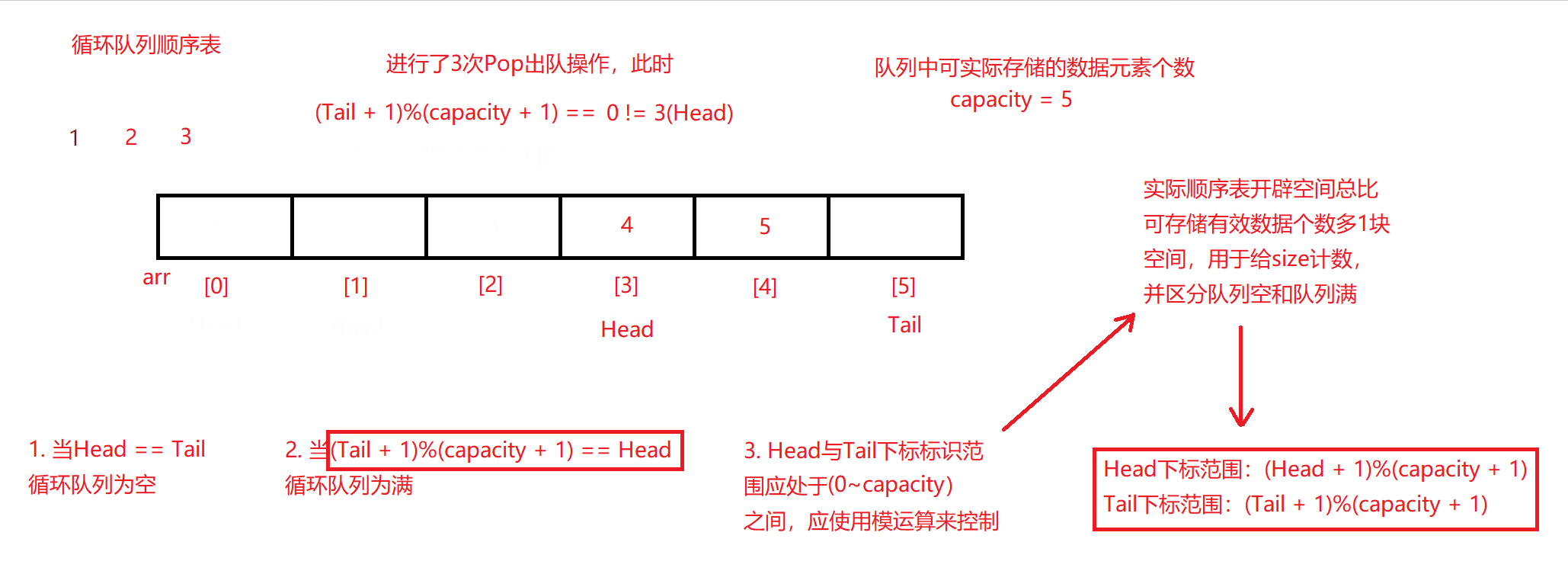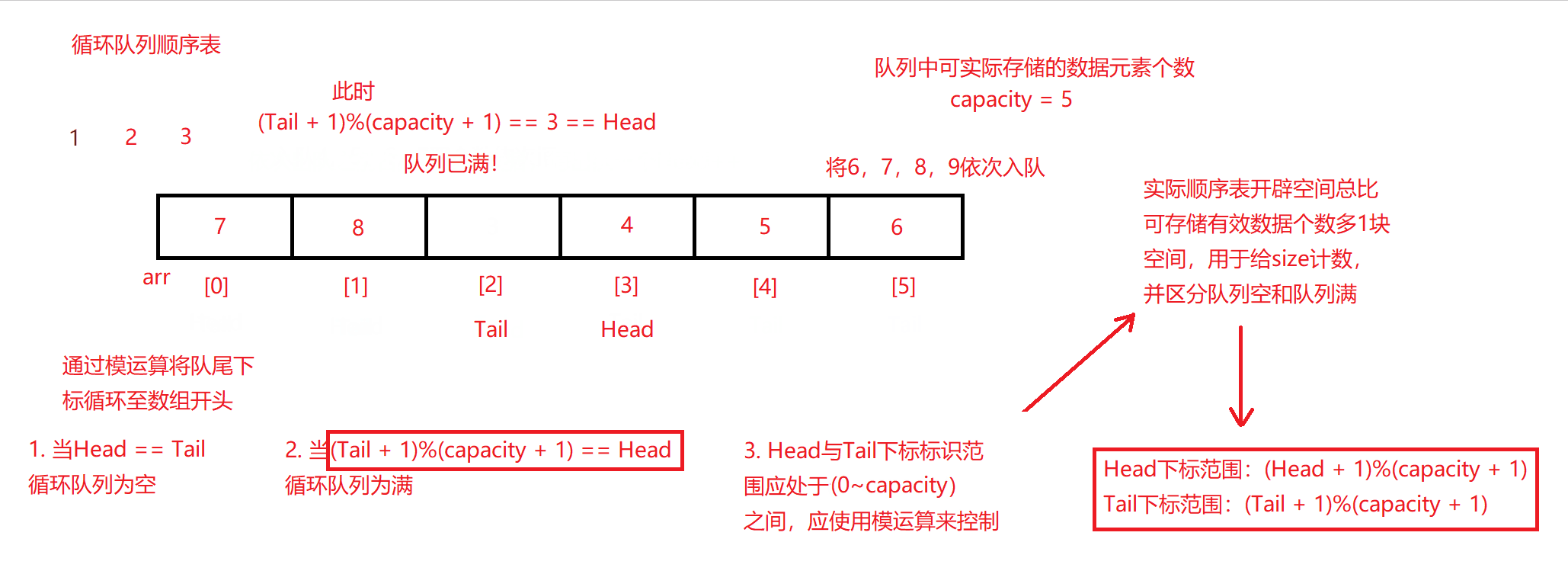
循环队列顺序表
循环队列的结构体定义与普通队列使用顺序表方式定义基本相同,其包含可动态扩容的内存空间指针(malloc函数在用户规定的循环队列大小一次性开辟好空间),以及一个队头和队尾下标分别用于头删出队和尾插入队操作。对于普通队列,数组容量capacity主要用于顺序表中数据的存储上限以及扩容更新,而在循环队列中,capacity用于给用户一次性定义好队列可实际存储的有效数据容量上限,且不可扩容,因为需要对空间的重复利用,所以当数据存储使队列满后,只能通过出队之前占用的空间,以使后续新的数据重新入队到重复的内存空间中。
循环队列结构定义
typedef int CRQueue; //循环队列存放的数值类型
typedef struct CirQueue //循环队列结构体
{
CRQueue* arr; //显示开辟顺序表实现队列——FIFO
int capacity; //队列可存储数据实际容量
int Head; //队头下标
int Tail; //队尾下标(为队尾元素的下一个位置)
}CRQ;
为了提高内存的数据存储空间利用率,仅根据所需容量开辟一定的内存空间,入队数据并直至开辟的空间占用满后,再通过将之前占用的数据依次出队,使后续数据能够入队并存放至之前已存储过数据开辟的空间而无需扩容。
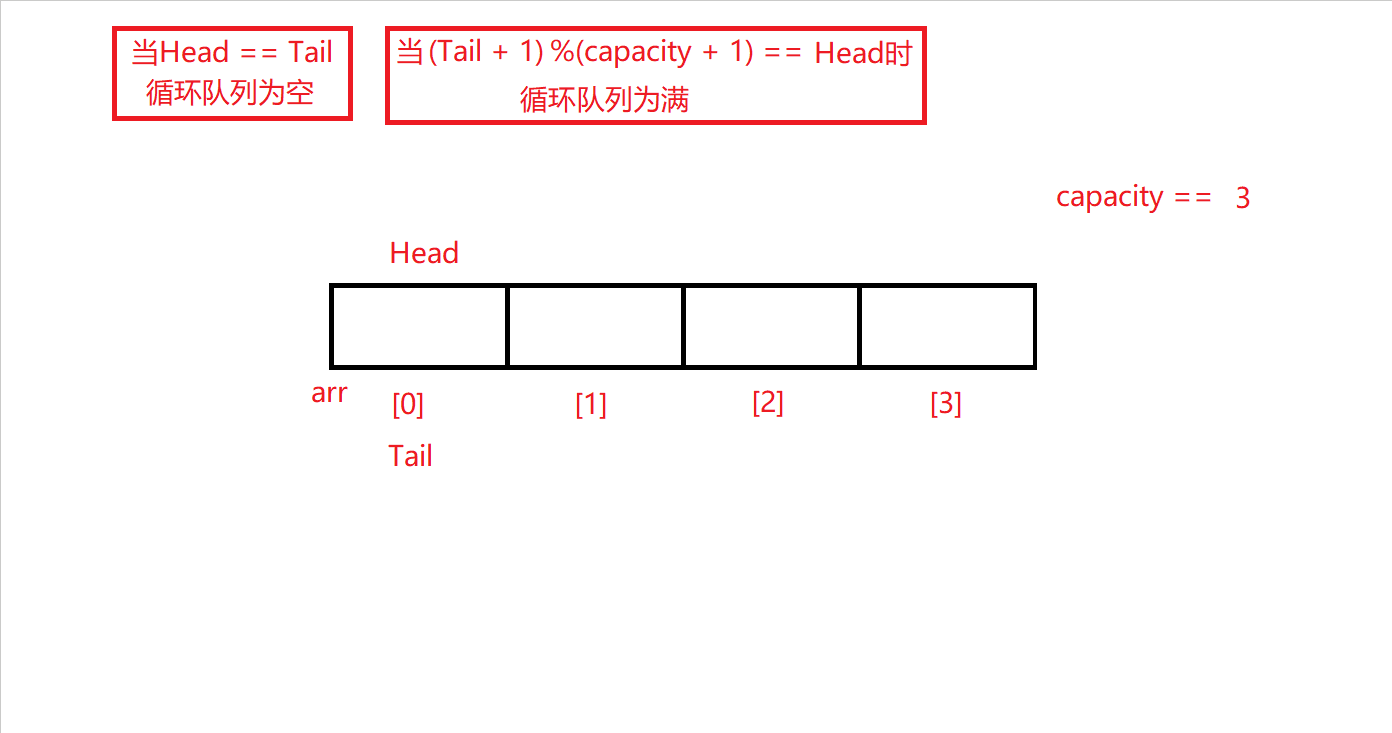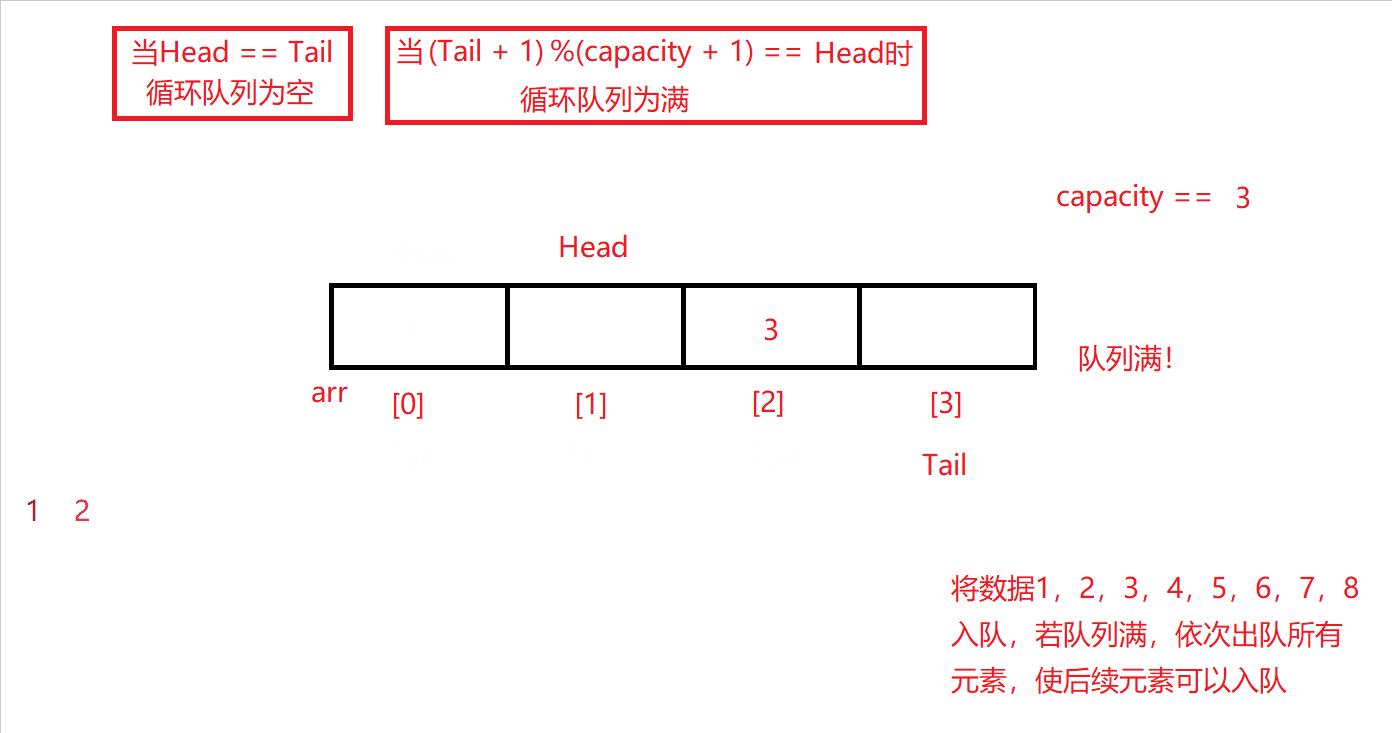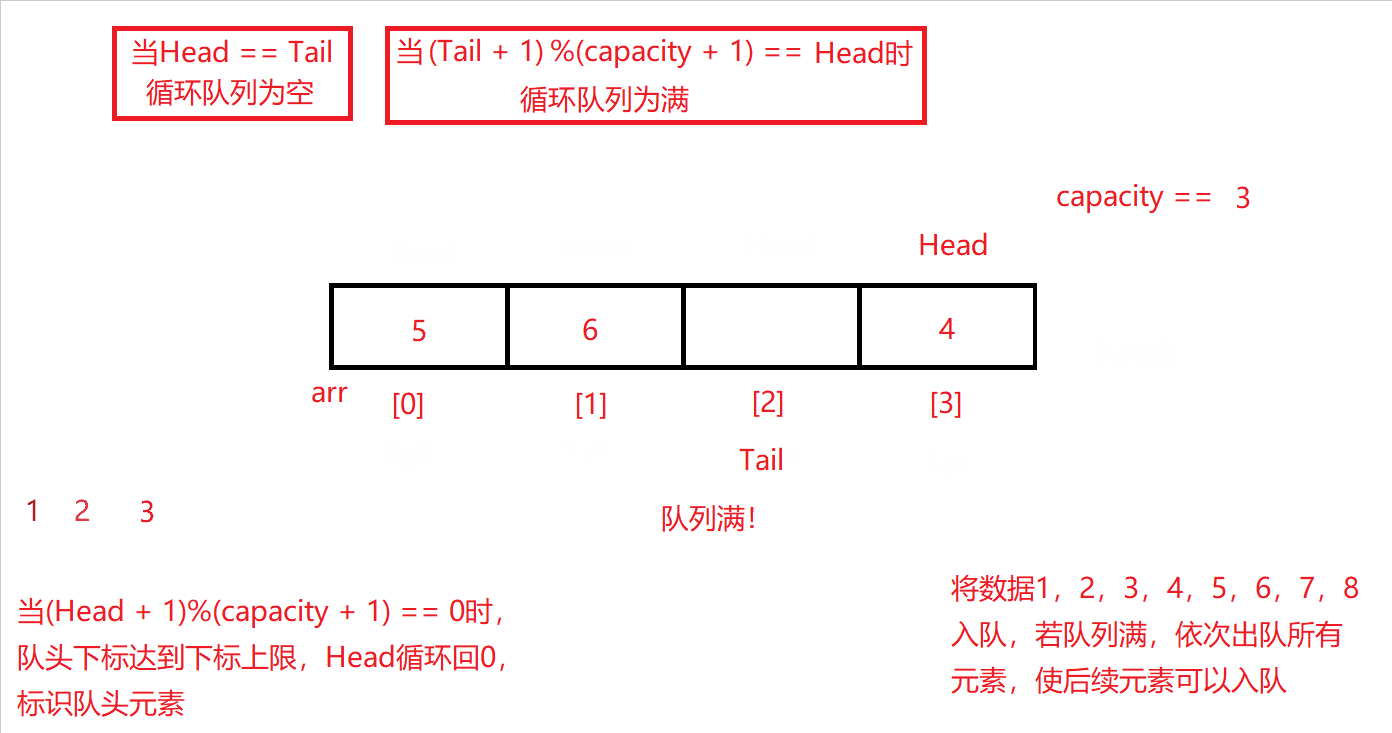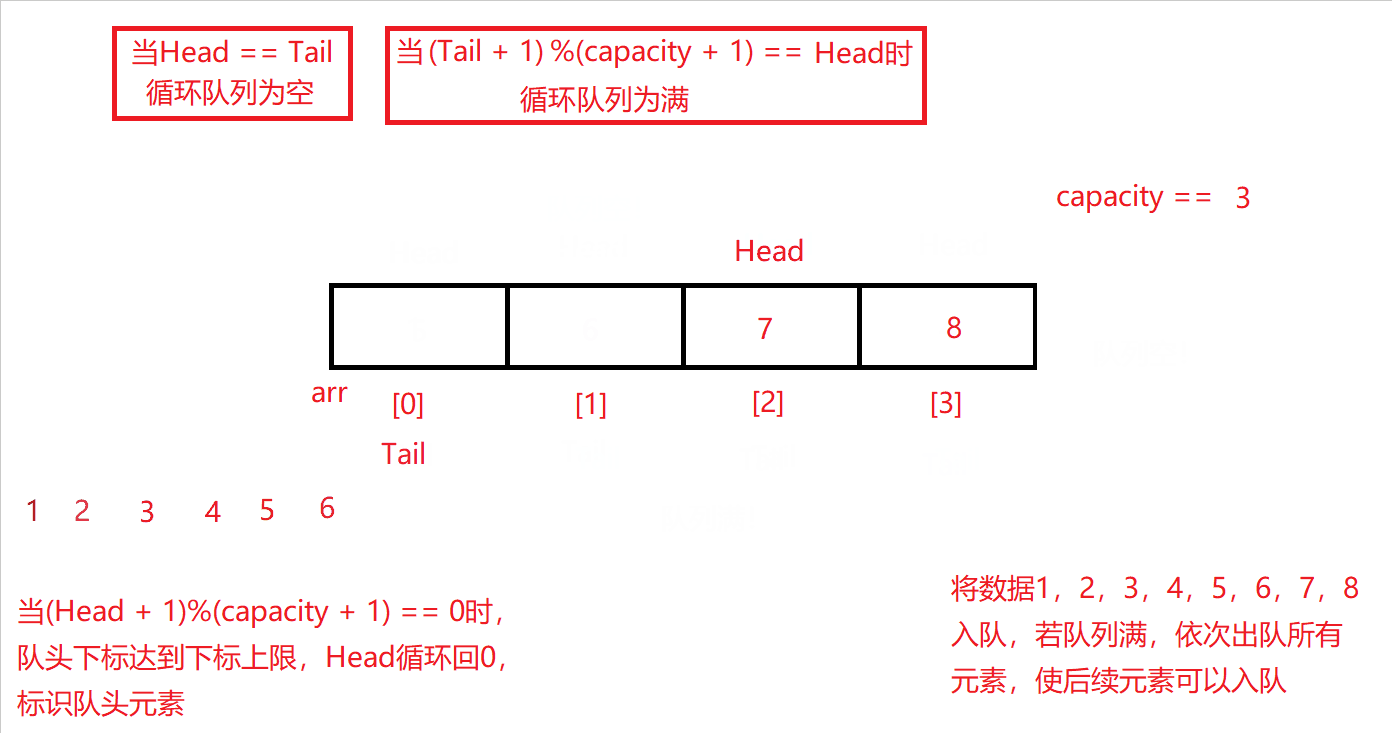
数据的入队和出队原理图如下
-
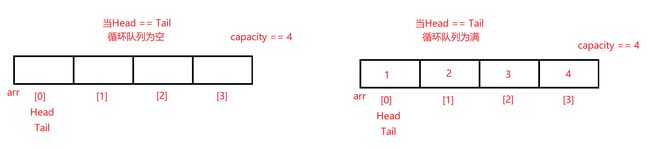
如上图所示,因为循环队列使用顺序表实现,数据除了要遵循连续依次存储外,标识内存空间的下标也需不超出开辟的数组空间。由图可知,队列的顺序表空间申请开辟的容量总比实际可存储数据多一个,因为如果不开辟出此看似“多余”的空间,就会使队列的满或空态充满歧义。
如下图所示:
- 还需注意的是,如同顺序表下个数据尾插的下标标识size或栈空间的数据压栈下标标识top,定义队尾待入队数据的下标标识定义为Tail,因为其所指向的空间是为了方便后续数据的尾插入队,所以其并非指向队列的最后一个数据元素,而是指向队尾元素的下一个位置。由此也可得知,如果不给循环队列的数组空间多额外开辟一个空间,则会出现以上队列空与队列满无法分清的情况。
循环队列空间初始化
CRQ* Create(int capacity) //传入需要开辟的循环队列数组空间,该空间为实际可存储数值容量,不包括多出的一块空间
{
CRQ* CirQueue = (CRQ*)malloc(sizeof(CRQ)); //循环队列结构体信息指针开辟空间
CirQueue->arr = (CRQueue*)malloc(sizeof(CRQueue) * (capacity + 1)); //开辟循环队列数组,开辟容量比实际数值存储容量多1个内存单元
assert(CirQueue);
CirQueue->Head = CirQueue->Tail = 0; //初始化数组头尾标识为0,此时循环队列为空
CirQueue->capacity = capacity; //初始化数组容量为实际可存储数据大小
return CirQueue;
}
- 可以看到,在函数内部进行了两次动态内存的显性开辟,第一次动态开辟了存储循环队列信息的结构体空间,该空间用于存储循环队列指针,以及标识队头下标,队尾下标和空间容量的三个整型数值共12个字节,将此结构体地址赋值给结构体指针,以待传回实参。第二次动态开辟即对结构体空间中指针指向的循环队列的存储空间进行初始化开辟,根据用户传入的所需队列实际存储容量capacity,并在此基础上+1以多开出一块内存给整个循环队列空间初始化,多开出的这一块内存已由前例阐述原因,不再赘述;其余数据直接置0,并返回该结构体指针地址。
循环队列入队
循环队列初始化完成,此时队头下标与队尾下标相等,队列为空,可入队数据。
循环队列判空函数
bool Empty(CRQ* obj)
{
assert(obj);
return obj->Head == obj->Tail; //当头与尾数值标识相等时,循环队列为空
}
以顺序表的方式进行入队操作,因为无需考虑到容量扩容的顾虑,每入队一个数据,将队尾标识Tail自增即可。前面已经提到需要注意两个点有两个:
- Tail虽然为队尾下标标识,但其指向的内存空间并非队尾数据所在,而是队尾数据的下一块连续的空间,以方便后续数据的入队。
- Tail下标标识范围不应超出开辟的数组空间,由前面队列初始化函数可知,用户传入容量capacity,而初始化实际开辟容量capacity + 1,所以下标范围限于0至capacity(下标总比数组容量小1,左闭右开区间)之间。为了控制Tail下标处于此范围,必须通过对Tail值的模运算以使Tail无论如何当数据入队自增时,都能在此范围间循环,达成控制数据在重复空间中存储和入队的需求。
循环队列入队代码
bool enQueue(CRQ* obj, CRQueue value)
{
assert(obj);
if (!Full(obj)) //如果循环队列不满
{
obj->arr[obj->Tail] = value; //将数据入队至队尾下标对应的空间上
obj->Tail = (obj->Tail + 1) % (obj->capacity + 1); //并且将队尾下标向后挪一位,且须保证其在开辟的数组空间范围内
return true;
}
return false; //循环队列满则入队失败,返回假
}
- 每次对数据于循环队列入队前都会进行队列空间的防满检测,判满原理其实与入队的队尾下标语句一致,且同样需要为了保证队尾下标循环在开辟的数组空间内移动。
队列判满函数
bool Full(CRQ* obj)
{
assert(obj); //当头数值标识+1,再模上数值容量+1(为了将头标识数值限定在指定范围内)
return ((obj->Tail + 1) % (obj->capacity + 1)) == obj->Head; //如果尾标识计算结果与头标识相等,则表示循环队列满
}
- 可以看到,控制Tail队尾下标标识的关键语句在于(obj->Tail + 1) % (obj->capacity + 1),因为队尾下标在数组中可标识范围为0~capacity(左闭右开区间),为了使其约束在该范围,通过使队尾下标Tail + 1与总容量capacity + 1模运算,即可使队尾下标向后移动一位并控制其不超出0~capacity范围,又可使Tail下标当达到下标上限时循环回去,若队列不满的情况下又从0开始向后续下标对应入队。
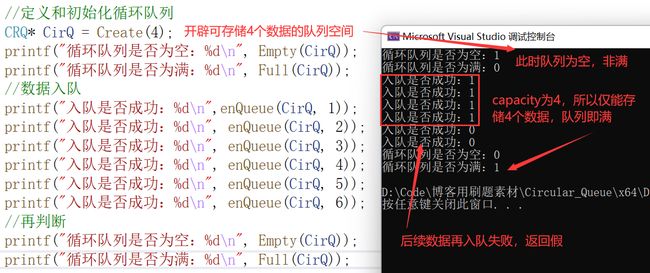
测试用例
//定义和初始化循环队列
CRQ* CirQ = Create(4); //开辟可容纳4个有效数据的循环队列空间,实际开辟了5个空间
printf("循环队列是否为空:%d\n", Empty(CirQ));
printf("循环队列是否为满:%d\n", Full(CirQ));
//数据入队
printf("入队是否成功:%d\n", enQueue(CirQ, 1));
printf("入队是否成功:%d\n", enQueue(CirQ, 2));
printf("入队是否成功:%d\n", enQueue(CirQ, 3));
printf("入队是否成功:%d\n", enQueue(CirQ, 4));
printf("入队是否成功:%d\n", enQueue(CirQ, 5));
printf("入队是否成功:%d\n", enQueue(CirQ, 6));
//再判断
printf("循环队列是否为空:%d\n", Empty(CirQ));
printf("循环队列是否为满:%d\n", Full(CirQ));
观察结果
循环队列出队
队列出队前先将队列的顺序表元素判空,如果数组非空,则从队头下标Head对应空间元素头删出队,每出队一个元素,Head自增。
循环队列出队函数
bool deQueue(CRQ* obj)
{
assert(obj);
if (!Empty(obj)) //如果循环队列不为空
{
//将队头下标向后挪一位,且须保证其在开辟的数组空间范围内
obj->Head = (obj->Head + 1) % (obj->capacity + 1);
return true;
}
return false; //循环队列空则出队失败,返回假
}
同入队的队尾下标控制范围一样,队头下标自增的过程中也需被限定在0~capacity的范围内,并使Head + 1与capacity + 1相模运算,即能满足前述要求,还能让队头下标达到下标上限后循环回下标0开始,再进行后续出队操作。
原理图如下:
测试用例
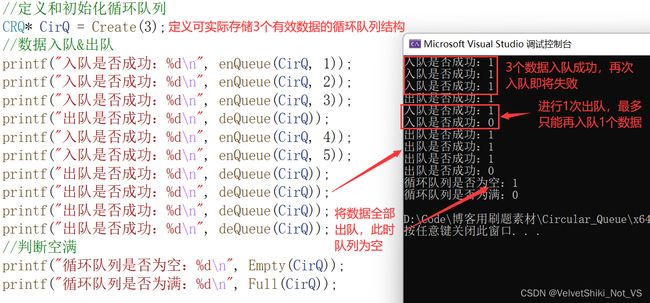
//定义和初始化循环队列
CRQ* CirQ = Create(3);
//数据入队&出队
printf("入队是否成功:%d\n", enQueue(CirQ, 1));
printf("入队是否成功:%d\n", enQueue(CirQ, 2));
printf("入队是否成功:%d\n", enQueue(CirQ, 3));
printf("出队是否成功:%d\n", deQueue(CirQ));
printf("入队是否成功:%d\n", enQueue(CirQ, 4));
printf("入队是否成功:%d\n", enQueue(CirQ, 5));
printf("出队是否成功:%d\n", deQueue(CirQ));
printf("出队是否成功:%d\n", deQueue(CirQ));
printf("出队是否成功:%d\n", deQueue(CirQ));
printf("出队是否成功:%d\n", deQueue(CirQ));
//判断空满
printf("循环队列是否为空:%d\n", Empty(CirQ));
printf("循环队列是否为满:%d\n", Full(CirQ));
观察结果
取队头和队尾数据
若队列不为空,队头下标Head对应的内存空间存储数值即为队头数据,取头但不出队;若队列为空,返回-1。
循环队列取队头函数
CRQueue GetFront(CRQ* obj)
{
assert(obj);
if (Empty(obj))
{
return -1; //如果循环队列为空,返回无意义值-1
}
return obj->arr[obj->Head]; //否则取队头下标所在空间的数值并返回
}
而对于取队尾数据,因为队尾下标标识空间数据为待存储入队数据,而非队尾数据,所以要进行特殊处理使函数得以返回队尾数据。
循环队列取队尾函数
CRQueue GetRear(CRQ* obj)
{
assert(obj);
if (Empty(obj))
{
return -1; //如果循环队列为空,返回无意义值-1
}
return obj->arr[(obj->Tail + obj->capacity) % (obj->capacity + 1)];
}
- 用队尾下标Tail+容量capacity和的结果,再模上容量capacity+1,就能得到尾下标前一个下标。
- 此处不能用直接对Tail-1再模容量+1的方式对前一个空间的队尾元素进行访问,因为这会涉及到C语言的负数模问题:语句(obj->Tail - 1) % (obj->capacity + 1)在C/C++中求模运算若对象是负数,则其求模仍为负数(如Tail == 0,(0 - 1) % 4 == -1,而不是3)。
测试用例
CRQ* CirQ = Create(3);
//数据入队&出队
enQueue(CirQ, 0);
printf("队头元素为:%d\n", GetFront(CirQ));
printf("队尾元素为:%d\n\n", GetRear(CirQ));
enQueue(CirQ, 1);
printf("队头元素为:%d\n", GetFront(CirQ));
printf("队尾元素为:%d\n\n", GetRear(CirQ));
enQueue(CirQ, 2);
printf("队头元素为:%d\n", GetFront(CirQ));
printf("队尾元素为:%d\n\n", GetRear(CirQ));
enQueue(CirQ, 3);
printf("队头元素为:%d\n", GetFront(CirQ));
printf("队尾元素为:%d\n\n", GetRear(CirQ));
观察结果
循环队列释放
循环队列的结构以顺序表为基本结构,所以其释放也要前后依次分为几个步骤:
- 先释放循环队列信息结构体中动态开辟的固定容量capacity数组空间。
- 再释放存储队列指针,队头队尾和容量标识的结构体信息空间。
- 将结构体指针置空并返回给实参。
循环队列释放函数
CRQ* Free(CRQ* obj)
{
assert(obj);
free(obj->arr); //将存放队列数据的数组空间释放
free(obj); //将保存循环队列信息的结构体空间释放
obj = NULL;
return obj;
}
步骤1和2的释放顺序不能颠倒,因为一旦先将结构体信息空间释放,则其中包含的队列指针arr便无法再定位寻找到,容易造成内存泄漏,所以需要特别注意。
测试用例
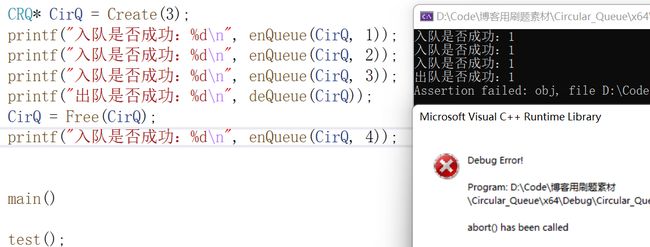
CRQ* CirQ = Create(3);
printf("入队是否成功:%d\n", enQueue(CirQ, 1));
printf("入队是否成功:%d\n", enQueue(CirQ, 2));
printf("入队是否成功:%d\n", enQueue(CirQ, 3));
printf("出队是否成功:%d\n", deQueue(CirQ));
//释放队列
CirQ = Free(CirQ);
printf("入队是否成功:%d\n", enQueue(CirQ, 4));
观察结果
可以看到将队列释放后,后续不能再完成入队,出队或取队头队尾等操作了,因为此时结构体指针和队列指针都已被释放且置空,传空指针进入函数内部即报错。
题目小练
一循环队列,其队头为Head,队尾为Tail,有效数据存储总个数为capacity,循环队列总容量为capacity + 1,则该循环队列内实际存储了多少数据?
A.(Tail - Head + capacity + 1) % (capacity + 2)
B.(Tail - Head + capacity + 1) % (capacity + 1)
C.(Tail - Head) % (capacity + 2)
D.(Tail - Head + capacity + 1) % capacity
答案:B
解释:
- 对于普通队列而言,有效长度直接让队尾减去队头下标即可得知实际个数,即Tail - Head,但是循环队列中Tail可能小于Head,减完之后可能是负数,所以需要加上总容量capacity + 1,此时结果刚好是队列中有效元素个数。
- 但如果Tail大于Head,结果恰好为是有效元素个数了,但是如果照搬上面的公式,再加capacity + 1后有效长度会超过capacity + 1,故需要%(capacity + 1)。
⭐括号匹配
括号是一对具有两个字符相互匹配成对的字符对,有小括号的 “(” 与 “)” 成对匹配,中括号 “[” 与 “]” 成对匹配以及大括号的 “{” 与 “}” 成对匹配。如果给定一系列具有不同括号样式(无规则)的字符数组,如果全部括号具有成对的匹配关系(不管是内匹配还是外匹配),则使用括号匹配函数返回真,否则返回假。
如以下几对括号序列:
char arr1[7] = "()[]{}"; //true
char arr2[5] = "(]{}"; //false
char arr3[5] = "({})"; //true
char arr4[5] = "([)]"; //false
char arr5[20] = "((([[{}]])))"; //true
char arr6[20] = "((([[{}]]]"; //false
char arr7[10] = "()]]{}"; //false
括号栈匹配算法
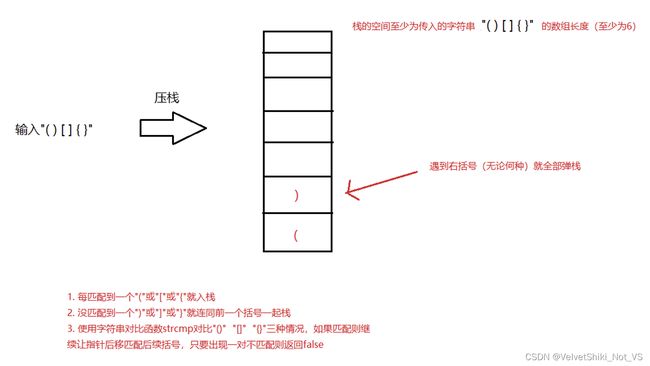
栈的结构是先进后出,如果将算法设计为遍历数组,遇到左括号就压栈,而遇到右括号就立即取栈顶元素与该右括号形成配对,并将这一对可能匹配或不匹配的括号与标准的三种类型(大中小括号)进行字符串比较strcmp(),如果两者值相同,即比对函数返回0则匹配成功;如果多对括号需要循环匹配与对比,则将遍历字符串的字符指针cur一直向后遍历至数组末的空值"\0",则停止遍历。
本章用到的栈指针和结构,接口函数等定义请参照本文开头给出的链接,其中包含了对于栈的数据类型别名以及函数的详细阐述,此处直接引用不再过多赘述。
原理图如下:
观察代码
bool BracketMatch(char* arr, int sz)
{
ST* match = StackInit(); //1. 存在于函数中的栈初始化函数,为每次不同的数组进入都将栈重新初始化,其中的数组a用于逐个存储arr中字符,并在Compare中比较标准括号对
assert(match);
SType* newcap = (SType*)realloc(match->a, sizeof(SType) * sz);
assert(newcap);
match->a = newcap; //2. 将栈最大容量匹配传入的字符串容量
match->capacity = sz;
char* cur = arr; //3. 定义遍历数组的字符指针
char Compare[3] = { 0 }; //4. 定义待存入遍历括号的数组与标准匹配括号进行对比
while (*cur != '\0') //5. 当遍历指针不指向空时,持续向后遍历括号类型
{
if (*cur == '(' || *cur == '[' || *cur == '{') //6. 当遇到左括号时就压栈
{
match->a[match->top] = *cur;
cur++;
match->top++;
continue;
}
if (*cur == ')' || *cur == ']' || *cur == '}') //7. 当遇到右括号时就取栈顶元素与当前括号匹配,并出栈
{
if (cur == arr) //8. 如果第一个括号就直接取到右括号,则直接判断该次括号匹配为假
{
return false;
}
match->a[match->top] = *cur;//9. 否则取当前括号与压入栈的栈顶扩招匹配在一起,存到对比数组Compare中
match->top++;
Compare[1] = STTop(match);
STPop(match);
Compare[0] = STTop(match);
STPop(match); //10. 将该取自当前指针所指右括号与取得栈顶的左括号与三类标准括号进行如下匹配
}
if (strcmp(Compare, "()") && strcmp(Compare, "[]") && strcmp(Compare, "{}"))
{ //11. 只要满足任一如上括号的匹配规则,则该次括号匹配为真,否则为假
return false;
}
cur++; //12. 将指针移向后一位,继续进行括号压栈和出栈匹配对比
}
if (match->top > 0) //13. 这个判断是为了防止只有左括号压入栈,而完全没有右括号的情况返回假
{
return false;
}
return true; //14. 如果将数组遍历完毕,所有括号都匹配成功,则该数组括号群匹配都成功,返回真
}
测试用例
//将如下包含不同类型括号序列的字符串传入括号栈匹配函数进行判定
char arr1[7] = "()[]{}"; //true
char arr2[5] = "(]{}"; //false
char arr3[5] = "({})"; //true
char arr4[5] = "([)]"; //false
char arr5[20] = "((([[{}]])))"; //true
char arr6[20] = "((([[{}]]]"; //false
char arr7[20] = "()]]{}"; //false
char arr8[20] = "{{{{{{{{{"; //false
int size = sizeof(arr1) / sizeof(arr1[0]);
//匹配成功打印true,否则打印假
if (BracketMatch(arr1, size))
{
puts("true");
}
else
{
puts("false");
}
观察结果
()[]{}匹配成功:true
(]{}匹配成功:false
({})匹配成功:true
([)]匹配成功:false
((([[{}]])))匹配成功:true
((([[{}]]]匹配成功:false
()]]{}匹配成功:false
{{{{{{{{{匹配成功:false
⭐后话
- 博客项目代码开源,获取地址请点击本链接:CSDN-循环队列设计,括号栈匹配VelvetShiki_Not_VS。
- 若阅读中存在疑问或不同看法欢迎在博客下方或码云中留下评论。
- 本章题目来源设计循环队列 - 力扣,有效的括号 - 力扣。
- 欢迎访问我的Gitee码云,如果对您有所帮助还可以一键三连,获取更多学习资料请关注我,您的支持是我分享的动力~