【论文解读】2017 STGCN: Spatio-Temporal Graph Convolutional Networks

一、简介

使用历史速度数据预测未来时间的速度。同时用于序列学习的RNN(GRU、LSTM等)网络需要迭代训练，它引入了逐步累积的误差，并且RNN模型较难训练。为了解决以上问题，我们提出了新颖的深度学习框架STGCN，用于交通预测。

二、STGCN模型架构

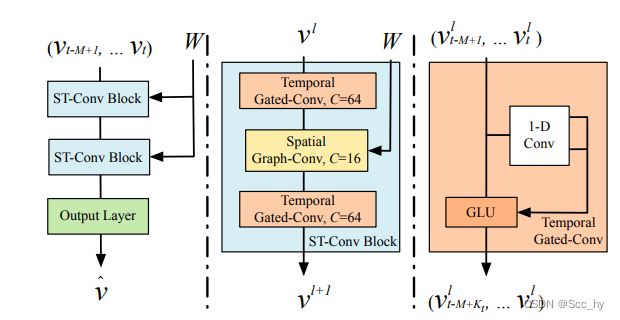
2.1 整体架构图示

2.2 ST-Conv blocks

符号	含义
M	历史时间序列长度
n	节点数
$C_i$	输入的channel 数
$C_o$	输出的channel 数

2.2.1 TemporalConv: Gated CNNs 用于提取时间特征

Note: nn.Conv2d的输入 channel在第一维度

$$\begin{gathered} [PQ]=Conv(x); \\ out=P\odot \sigma (Q) \end{gathered}$$

• $x\in {\mathbb{R}}^{C_i\times M\times n}$
• $[\text{P Q}]\in {\mathbb{R}}^{2C_o\ast (M-K_t+1)\times n}$

示例代码:

class TCN(nn.Module):
    def __init__(self, c_in: int, c_out: int, dia: int=1):
        """TemporalConvLayer
        input_dim:  (batch_size, 1, his_time_seires_len, node_num)
        sample:     [b, 1, 144, 207]
        Args:
            c_in (int): channel in
            c_out (int): channel out
            dia (int, optional): 空洞卷积大小. Defaults to 1.
        """
        super(TCN, self).__init__()
        self.c_out = c_out * 2
        self.c_in = c_in
        self.conv = nn.Conv2d(
            c_in, self.c_out, (2, 1), 1, padding=(0, 0), dilation=dia
        )

    def forward(self, x):
        # [batch, channel, his_n, node_num] 
        #  仅在时间维度上进行卷积 
        c = self.c_out//2
        out = self.conv(x)
        if len(x.shape) == 3: # channel, his_n, node_num
            P = out[:c, :, :]
            Q = out[c:, :, :]
        else:
            P = out[:, :c, :, :]
            Q = out[:, c:, :, :]
        return P * torch.sigmoid(Q)

2.2.2 SpatialConv: Graph CNNs 提取空间信息

迭代定义的切比雪夫多项式

$$out={\Theta }_{\ast \mathcal{G}}x=\sum _{k=0}^{K-1}{\theta }_k{T}_k(\tilde{L})x=\sum _{k=0}^{K-1}{W}^{K,l}{z}^{k,l}$$

• $Z^{0,l}=H^l$
• $Z^{1,l}=\tilde{L}\cdot H^l$
• $Z^{k,l}=2\cdot \tilde{L}\cdot Z^{k-1,l}-Z^{k-2,l}$
• $\tilde{L}=2\left(I-{\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}\right)/{\lambda }_{max}-I$

论文： Recursive formulation for fast filtering

示例代码:

class STCN_Cheb(nn.Module):
    def __init__(self, c, A, K=2):
        """spation cov layer
        Args:
            c (int): hidden dimension
            A (adj matrix): adj matrix
        """
        super(STCN_Cheb, self).__init__()
        self.K = K
        self.lambda_max = 2
        self.tilde_L = self.get_tilde_L(A)
        self.weight = nn.Parameter(torch.empty((K * c, c)))
        self.bias = nn.Parameter(torch.empty(c))
        stdv = 1.0 / np.sqrt(self.weight.size(1))
        self.weight.data.uniform_(-stdv, stdv)

    def get_tilde_L(self, A):
        I = torch.diag(torch.Tensor([1] * A.size(0))).float().to(A.device)
        tilde_A = A + I 
        tilde_D = torch.diag(torch.pow(tilde_A.sum(axis=1), -0.5))
        return 2 / self.lambda_max * (I - tilde_D @ tilde_A @ tilde_D) - I

    def forward(self, x):
        # [batch, channel, his_n, node_num] -> [batch, node_num, his_n, channel] -> [batch, his_n, node_num, channel] 
        x = x.transpose(1, 3)
        x = x.transpose(1, 2)
        output = self.m_unnlpp(x)
        output = output @ self.weight + self.bias
        output = output.transpose(1, 2)
        output = output.transpose(1, 3)
        return torch.relu(output) 

    def m_unnlpp(self, feat):
        K = self.K
        X_0 = feat
        Xt = [X_0]
        # X_1(f)
        if K > 1:
            X_1 = self.tilde_L @ X_0
            # Append X_1 to Xt
            Xt.append(X_1)
        # Xi(x), i = 2...k
        for _ in range(2, K):
            X_i =  2 * self.tilde_L @ X_1 - X_0
            # Add X_1 to Xt
            Xt.append(X_i)
            X_1, X_0 = X_i, X_1
        # 合并数据
        Xt = torch.cat(Xt, dim=-1)
        return Xt

2.2.3 ST-Block

组合TCN和STCN_Cheb
$$v^{l+1}={\Gamma }_{1\ast \mathcal{T}}^l\text{ReLU}({\Theta }_{\ast \mathcal{G}}^l({\Gamma }_{0\ast \mathcal{T}}^l{v}^l))$$

• ${\Gamma }_{0\ast \mathcal{T}}^l{v}^l$: 第一个TCN
• ${\Theta }_{\ast \mathcal{G}}^l$ : STCN_Cheb
• ${\Gamma }_{1\ast \mathcal{T}}^l{v}^l$: 第二个TCN

class STBlock(nn.Module):
    def __init__(
        self,
        A,
        K=2,
        TST_channel: List=[64, 16, 64]
        T_dia: List=[2, 4]
    ):
        # St-Conv Block1[  TCN(64, 16*2)->SCN(16, 16)->TCN(16, 64*2) ] 
        super(STBlock, self).__init__()
        self.T1 = TCN(TST_channel[0], TST_channel[1], dia=T_dia[0])
        # STCN_Cheb out have relu
        self.S = STCN_Cheb(TST_channel[1], Lk=A, K=K)
        self.T2 = TCN(TST_channel[1], TST_channel[2], dia=T_dia[1])

    def forward(self, x):
        return self.T2(self.S(self.T1(x)))

三、简单复现

复现可以看笔者的github: train.ipynb
用的数据是metr-la.h5