Gray Code
https://leetcode.com/problems/gray-code/
The gray code is a binary numeral system where two successive values differ in only one bit.
Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.
For example, given n = 2, return [0,1,3,2]. Its gray code sequence is:
00 - 0 01 - 1 11 - 3 10 - 2
Note:
For a given n, a gray code sequence is not uniquely defined.
For example, [0,2,3,1] is also a valid gray code sequence according to the above definition.
For now, the judge is able to judge based on one instance of gray code sequence. Sorry about that.
解题思路:
这道题目在leetcode上被标注为中等难度,ac率也超过了30%。开始以为很简单,只是一般的permutation,用DFS或者BFS。后来发现这道题和一般的permutation不同,相邻的code只能有一个bit不一样。
首先把n=3的时候情况写下来,结果半天没发现规律。
000
001
011
010
110
111
101
100
后来去wiki上看到下面的图
| 2-bit | 4-bit |
|---|---|
| 00 01 11 10 |
0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 |
| 3-bit | |
| 000 001 011 010 110 111 101 100 |
http://en.wikipedia.org/wiki/Gray_code
从左到有竖着看每位,大概有以下的规律:
可以将每种组合看成2^n行,n列的一个二维数组。我们竖着看所有行的第一列,有4个0,然后是4个1。
第二列,有2个0,然后是4个1,2个0.
第三列,有1个0,然后2个1,2个0,2个1,1个0。
可以总结出规律,第一列是2^n-1个0,然后是2^n-1个1。第二列往后的第i列,首先出现Math.pow(2, n - 1 - i)个0,然后是Math.pow(2, n - 1 - i + 1)个1和0交替出现,直到最后。
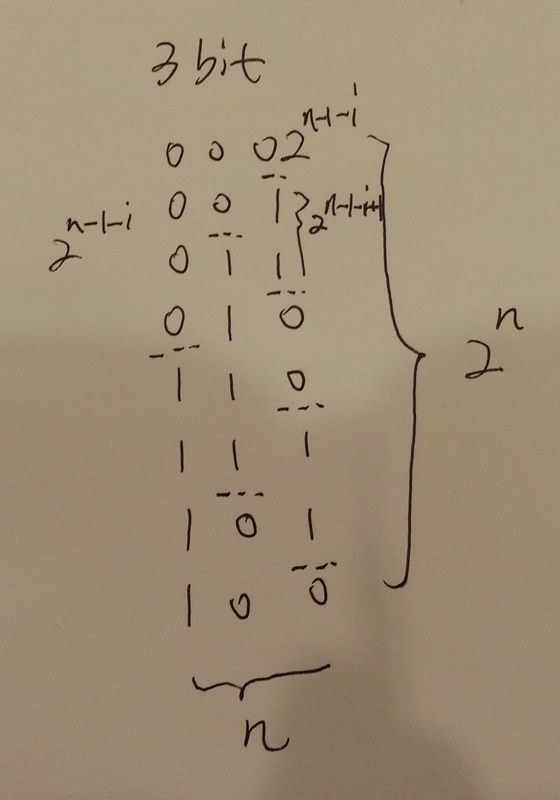
上图是手画的,当n=4的时候,我们可以验证一下这样的规律。
规律找到后,代码还是相对容易的。有些复杂的是,如何交替实现上面的规则。我们可以对第一列写死,一半0然后一半1。第二列往后,首先Math.pow(2, n - 1 - i)个0,然后后面看行数减去Math.pow(2, n - 1 - i)个0的差,是Math.pow(2, n - 1 - i + 1)的整数倍(比如上图第二列4个1,也就是4的整数倍),carry就++,然后carry去取2的模,来控制是输出0还是1.
public class Solution { public List<Integer> grayCode(int n) { List<Integer> result = new ArrayList<Integer>(); if(n == 0){ result.add(0); return result; } int codeSize = (int)Math.pow(2, n); StringBuffer[] codes = new StringBuffer[codeSize]; for(int i = 0; i < n; i++){ int carry = 0; for(int j = 0; j < codeSize; j++){ if(i == 0){ codes[j] = new StringBuffer(n); } //竖着看,第i位的bit遵从以下的规律 //首先出现Math.pow(2, n - 1 - i)个0,然后是Math.pow(2, n - 1 - i + 1)个1和0交替出现,直到最后 if(j >= (int)Math.pow(2, n - 1 - i) && (j - (int)Math.pow(2, n - 1 - i)) % ((int)Math.pow(2, n - 1 - i + 1)) == 0){ carry++; } //这种控制输出0和1的方法也是一个技巧 codes[j].append(carry % 2); } } //最后二进制转十进制的方法懒得写了 for(int i = 0; i < codeSize; i++){ result.add(new java.math.BigInteger(codes[i].toString(), 2).intValue()); } return result; } }
我们可以看到上面的解法比较慢,需要的时间复杂度为O(n*2^n)。
随后在网上看到了一种极为巧妙而简单的解法,如下图。
可以看到,第n个的gray code由两部分组成。第一部分,在n-1的基础上,前面直接加上0(这时它的十进制值是完全不变的);第二部分,将n-1的gray code倒置,再在前面加上1。
如果不google,这个规律是怎么得出来的?看出来,第一位就是0和1各一半,后面的是以中心的轴对称。完全是考验观察力了。
public class Solution { public List<Integer> grayCode(int n) { List<Integer> result = new ArrayList<Integer>(); // if(n == 0){ // result.add(0); // return result; // } result.add(0); for(int i = 0; i < n; i++){ int headBit = 1 << i; //从后往前 for(int j = result.size() - 1; j >= 0; j--){ result.add(result.get(j) + headBit); } } return result; } }
我只看出了第一个解法。这个代码是看了人家的解法后,再写出来的。与我的代码比,有几点好处。首先,它直接用位运算,排列的时候就转化成了十进制数,省去了最后的过程。第二,求第i次gray code的时候,其实只要在前面已有的i-1次gray code上,从后往前在前面都加上1就可以了。也就是只操作镜像后的部分,前面的留着就行了,因为加上0后,二进制排序变化,但是十进制的值不变。
这个解法的内层循环,最后result的size会达到2^n,从1开始增长,是指数级的。所以可以认为时间复杂度也是O(n*2^n),但是考虑到内层循环实际是一个等比数列了,总的循环次数就是1...2^n求和,仅仅为O(2^n - 1)。
这道题很巧妙,很看观察力,而不是用普通的死记硬背的DFS或者BFS求解,需要记住。