解析基因影响:孟德尔随机化的创新思维
一、引言
在当今的遗传学和生物学研究中,我们对基因对个体特征和性状的影响的理解变得更加深入。然而,基因影响的复杂性和多样性给我们带来了巨大的挑战。为了更好地揭示基因影响的本质和机制,我们需要采用创新的研究思维和方法。
本文的目的是探讨使用孟德尔随机化的创新思维来解析基因影响的重要性。孟德尔随机化是一种基于自然突变和基因重新组合的实验设计,通过利用随机分配的基因组合,帮助我们确定基因与个体差异之间的因果关系[1]。与传统的关联研究相比,孟德尔随机化能够提供更可靠的证据和更准确的结果,从而帮助我们更好地理解基因对个体特征和疾病风险的影响。
二、孟德尔随机化是什么?
「孟德尔随机化(Mendelian randomization,MR)」 是一种流行遗传学方法,用于评估观察研究中的因果关系。它利用遗传变异作为工具变量,通过选择与暴露因素相关的遗传变异来模拟一种随机对照试验的效果。孟德尔随机化的原理基于孟德尔遗传学定律,该定律指出遗传变异在一定程度上是随机分配的。
孟德尔随机化主要依赖于三个核心假设:
- 第一,工具变量(常用的是遗传变异)与暴露因素之间存在关联性;
- 第二,工具变量仅通过暴露因素对观察结果产生影响,而不与其他混淆因素关联;
- 第三,工具变量的分配是随机的,不受观察结果的影响。通过满足这些假设条件,可以利用工具变量对观察结果进行因果推断。
在孟德尔随机化中,研究者选择与暴露因素相关的遗传变异作为工具变量,并利用这些变异对观察结果进行分析。通常,线性回归模型被用来评估工具变量与观察结果之间的因果关系。通过比较使用工具变量的效应估计值,可以得出关于暴露因素对特定结果的因果效应的初步结论。
孟德尔随机化方法广泛应用于评估治疗方法、药物效果、生物途径和疾病相关性等方面。它提供了一种处理因果问题的替代方案,尤其在无法进行随机对照试验的情况下,可以提供一定程度的因果推断支持。然而,孟德尔随机化也有一些局限性,包括遗传变异选择、遗传变异与观察结果之间的多样性和复杂性等问题。因此,适当选择合适的工具变量和数据源,并结合其他证据和领域知识进行结果的解释和验证是至关重要的。
三、MR原理和假设?
3.1 原理
- 选择合适的工具变量:在孟德尔随机化中,研究者选择与暴露因素相关的遗传变异作为工具变量。
- 工具变量与暴露因素之间的关联:工具变量应该与暴露因素相关,即工具变量能够预测或影响暴露因素的变化。
3.2 假设:
- 工具变量与观察结果之间的因果关系仅通过暴露因素:这是孟德尔随机化的核心假设,即工具变量通过影响暴露因素来间接影响观察结果,而不是通过其他混淆因素或逆向因果机制的影响。
- 工具变量的分配是随机的:工具变量的分配应该是随机的,不受观察结果的影响。这意味着工具变量在人群中的分布与观察结果之间不应存在系统性的关联。
四、MR分析流程是?
- 确定研究目标:明确研究的目的和问题,确定要评估的暴露因素和观察结果。
- 选择工具变量:选择与暴露因素相关的遗传变异作为工具变量。这些遗传变异在理论上应该只通过暴露因素对观察结果产生影响,而不与其他混淆因素相关。
- 评估工具变量与暴露因素的关联性:使用基因关联研究或其他相关数据来评估工具变量与暴露因素之间的关联性。这可以通过查看工具变量与暴露因素的遗传关联统计指标(如p值、OR等)来实现。
- 校正混淆因素:根据需要,进行处理以控制或校正可能的混淆因素。这可能涉及到使用其他相关的遗传变异或调整观察数据的其他个体特征。
- 评估工具变量与观察结果的因果关系:使用适当的统计方法,如仪器变量方法中的线性回归模型,评估工具变量与观察结果之间的因果关系。这可以通过比较工具变量对观察结果的效应估计来实现。
- 进行敏感性分析:进行敏感性分析来评估结果对可能偏倚的鲁棒性。这可能涉及到检查结果在不同的统计模型和假设条件下的变化情况,以及对可能的混淆因素进行进一步的校正。
- 结果解释和推断:结合其他证据和领域知识,对结果进行解释和推断。这涉及到综合考虑孟德尔随机化分析的结果、假设和步骤的限制,并将其与其他研究结果和背景知识相结合,得出初步的因果推断。
五、浅析范例论文
5.1 确定研究目标和研究设计

「A. MR分析依赖于三个核心假设。」
在进行MR分析时,有三个核心假设需要满足:
- 遗传变异(SNPs)与暴露因素(exposure)之间存在关联。
- 遗传变异(SNPs)与结局(outcome)之间存在关联。
- 遗传变异(SNPs)与结局(outcome)之间的关联完全通过暴露因素(exposure)进行传递。
「B. 研究设计草图」
该研究设计采用了双向MR方法,其中红色代表了正向MR分析,以重症COVID-19为暴露因素(exposure),以白细胞端粒长度(leukocyte telomere length,LTL)为结局(outcome)。蓝色代表了反向MR分析,以白细胞端粒长度(LTL)为暴露因素(exposure),以重症COVID-19为结局(outcome)。在该研究中,采用了单核苷酸多态性(single-nucleotide polymorphisms,SNPs)和连锁不平衡(linkage disequilibrium,LD)作为关联分析的工具。
5.2 选择工具变量
为了进行MR分析,从两个不同的GWAS总结统计结果中选择了适当的工具变量。
- 在基因组范围内达到显著性水平(
p < 5 × 10^(-8))的SNPs被选出。 - 在欧洲1000人基因组参考组中,根据相关不平衡(LD)的度量
r^2 > 0.01,筛选出适当的SNPs。 - 排除了与结果相关且
p < 5 × 10^(-8)的SNPs。在协调暴露和结果数据时,被移除了拥有中等等位基因频率的回文SNPs(即两个等位基因互为补反)。
5.3 重症COVID-19的数据来源和工具变量的选择
使用了一个由15个欧洲队列组成的集中式荟萃分析数据,用于关键病重COVID-19的分析 [36]。该数据集来源于COVID-19宿主遗传学计划(COVID-19HGI),包括了5,101例病重COVID-19患者和1,383,241名对照个体。 
病重COVID-19病例包括因与实验室确诊的SARS-CoV-2感染相关的症状而住院,并需要呼吸支持或其主要死因为COVID-19的患者[36]。对照组选取为通过基因祖源匹配的无已知SARS-CoV-2感染个体,如果有这样的信息[36]。在该GWAS分析中,鉴定了与关键病重COVID-19相关的15个SNPs,并将其选为工具变量。其中,有9个SNP的p值超过了5 × 10^(-8),因此被排除。因此,最终包括6个变异体作为MR分析中的遗传工具.
5.4 用于LTL的数据来源和工具变量的选择
LTL的数据来源于英国生物库(UK Biobank),包括472,174名参与者[28](附录表格1)。对于反向MR分析,我们从197个与LTL相关的独立位点中选择了适当的工具变量。其中,2个p值大于5 × 10^(-8)的SNPs被排除,使用PLINK clumping工具去除了65个r^2 > 0.01的SNPs,因其具有潜在的多效性位点而移除了17个SNPs,还有16个SNPs由于缺失MR分析所需的信息而被排除。最终,选择了97个工具变量用于MR分析. 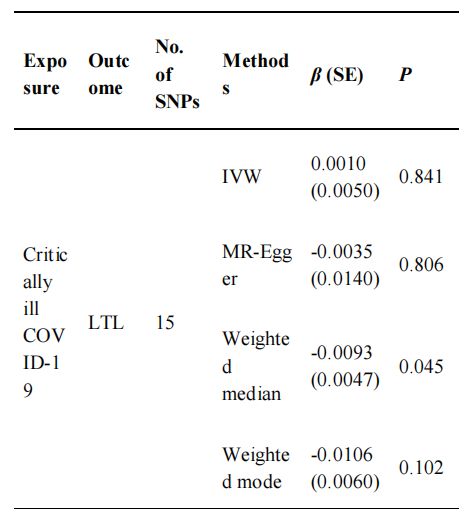
5.5 统计分析
使用随机效应的反向方差加权(IVW)方法作为主要的统计方法来估计关键病重COVID-19和LTL之间潜在的双向因果关系。IVW方法基于一个假设,即MR的所有核心假设都是有效的。然而,工具变量通过其他途径影响结果,表明存在潜在的水平多效应,并且IVW的因果估计可能存在偏倚。因此,我们还通过使用MR-Egger和加权中位数 方法进行敏感性分析,即使存在无效的SNPs,也可以准确估计因果关系。
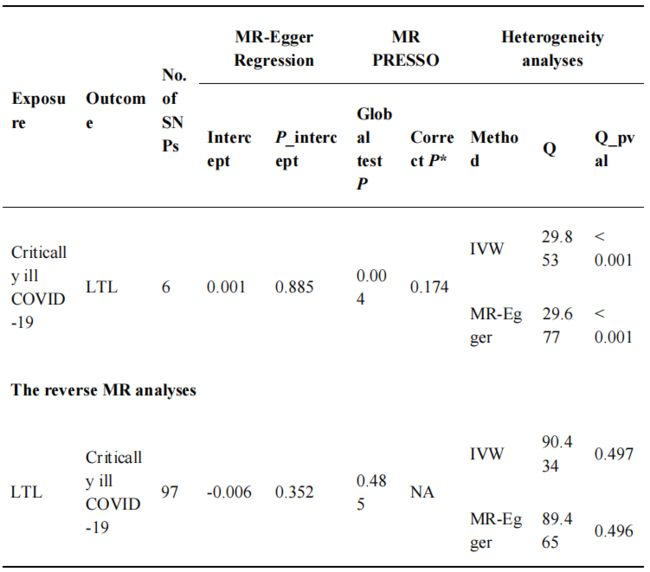
由于MR分析依赖于三个核心IV假设(图1)的主要分析,我们报告了用于评估这些假设或证明其有效性的方法。对于相关性假设,计算R2以表示遗传变异解释暴露变量方差的比例。我们估计F统计量来评估IV和感兴趣暴露风险之间的工具强度。F < 10表示工具强度较弱。对于排除限制假设,使用MR-Egger回归截距及其95%置信区间来研究由定向多效性引起的因果估计偏差程度。此外,还通过采用MR-PRESSO全局检验评估水平多效应,并通过MR-PRESSO离群SNP检验排除离群SNPs。此外,除去离群IVs后,我们还检查与先前结果相比是否存在显著差异。我们还通过Cochran’s Q统计量和漏斗图对IVW和MR-Egger方法进行异质性检验。最后,进行了几项敏感性分析,例如逐一排除分析和单个SNP分析,以确定单个SNP是否影响主要因果关系。
对于二元结果,使用比值比(OR)和95%置信区间(CI)来估计因果关系的程度。二元和连续结果的因果估计、p值、beta值及其标准误差也被呈现。 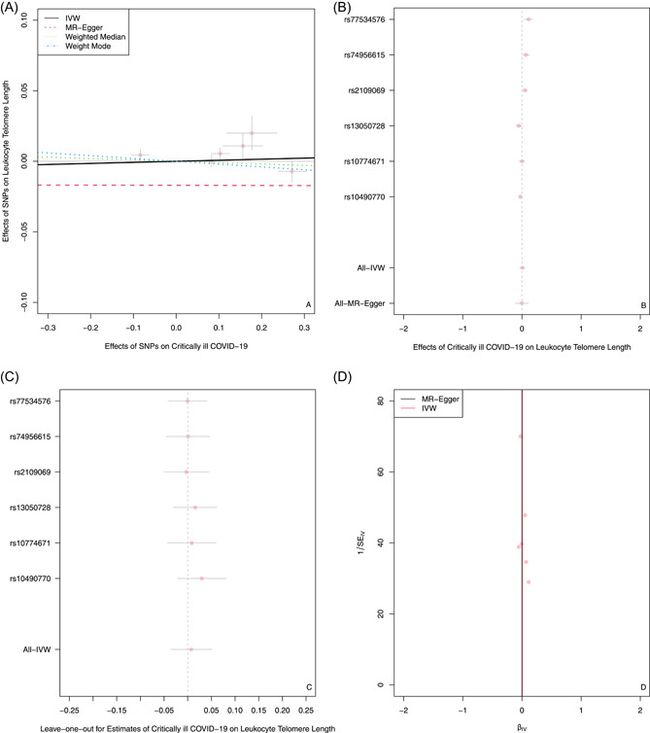
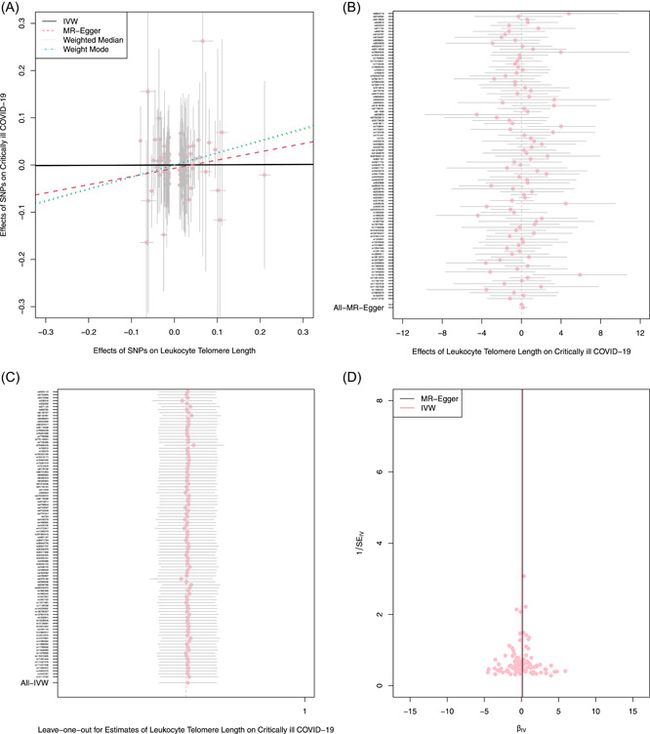
这里先暂时卖一个关子,如果有需要我复刻该文章的请私信我扣1,然后只对这个图很感兴趣和R语言怎么进行MR分析的扣2.欢迎和我互动,原创不易,请给个关注和点赞,谢谢!
六、应用范围
治疗效果评估:孟德尔随机化可以用于评估特定治疗或干预措施对特定疾病或健康结果的真实因果效应。通过使用工具变量作为干预的代理,可以模拟随机对照试验的结果。
药物效果评估:孟德尔随机化方法可以用于评估药物使用和药物治疗对特定疾病或健康结果的因果影响。研究者可以利用与药物作用相关的遗传变异作为工具变量来推断药物的效应。
生物途径评估:孟德尔随机化方法可以用于研究生物途径和机制的因果关系。通过选择与生物途径相关的遗传变异作为工具变量,可以评估该途径对特定疾病或生理功能的影响。
疾病相关性评估:孟德尔随机化方法可以用于评估与特定疾病相关的因素和风险因素之间的因果关系。通过利用与这些因素相关的遗传变异作为工具变量,可以评估其对疾病风险的影响。
参考文献:
- Birney E. Mendelian Randomization. Cold Spring Harb Perspect Med. 2022;12(4):a041302. Published 2022 May 17. doi:10.1101/cshperspect.a041302
- Huang D, Lin S, He J, Wang Q, Zhan Y. Association between COVID-19 and telomere length: A bidirectional Mendelian randomization study. J Med Virol. 2022;94(11):5345-5353. doi:10.1002/jmv.28008