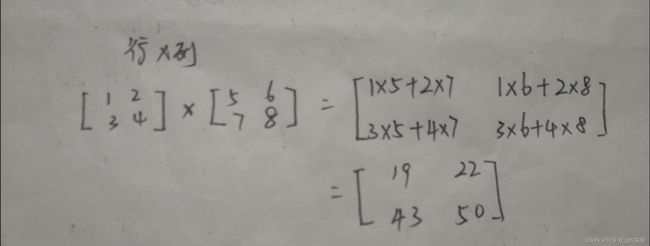（记录）Python机器学习——Numpy数组的高级操作

文章目录

前言

一、堆叠操作

(2)vstack

(3)尝试

二、比较、掩码和布尔逻辑

（1）比较

（2）布尔数组作掩码

（3）布尔逻辑

（4）尝试

三、花式索引与布尔索引

（1）花式索引

 （2）布尔索引

（3）尝试

四、广播机制

（1）广播

（3）尝试

五、线性代数

（1）numpy的线性代数

1.dot()

2.det()

3.inv()

4.solve()

5.matmul()

6.svd()

（2）尝试

---

---

前言

上一篇 Numpy基础

http://t.csdn.cn/eNkIt

---

一、堆叠操作

stack的意思是堆叠的意思，所谓的堆叠就是将两个ndarray对象堆叠在一起组合成一个新的ndarray对象。根据堆叠的方向不同分为hstack以及vstack两种。

（1）hstack

假如你是某公司的HR，需要记录公司员工的一些基本信息。可能你现在已经记录了如下信息：

工号	姓名	出生年月	联系电话
1	张三	1988.12	13323332333
2	李四	1987.2	15966666666
3	王五	1990.1	13777777777
4	周六	1996.4	13069699696

世界上没有不变的需求，你的老板让你现在记录一下公司所有员工的居住地址和户籍地址，此时你只好屁颠屁颠的记录这些附加信息。然后可能会有这样的结果：

居住地址	户籍地址
江苏省南京市禄口机场宿舍202	江西省南昌市红谷滩新区天月家园A座2201
江苏省南京市禄口机场宿舍203	湖南省株洲市天元区新天华府11栋303
江苏省南京市禄口机场宿舍204	四川省成都市武侯祠安置小区1栋701
江苏省南京市禄口机场宿舍205	浙江省杭州市西湖区兴天世家B座1204

接下来你需要把之前记录的信息和刚刚记录好的附加信息整合起来，变成酱紫：

工号	姓名	出生年月	联系电话	居住地址	户籍地址
1	张三	1988.12	13323332333	江苏省南京市禄口机场宿舍202	江西省南昌市红谷滩新区天月家园A座2201
2	李四	1987.2	15966666666	江苏省南京市禄口机场宿舍203	湖南省株洲市天元区新天华府11栋303
3	王五	1990.1	13777777777	江苏省南京市禄口机场宿舍204	四川省成都市武侯祠安置小区1栋701
4	周六	1996.4	13069699696	江苏省南京市禄口机场宿舍205	浙江省杭州市西湖区兴天世家B座1204

看得出来，你在整合的时候是将两个表格（二维数组）在水平方向上堆叠在一起组合起来，拼接成一个新的表格（二维数组）。像这种行为称之为hstack（horizontal stack）。

NumPy提供了实现hstack功能的函数叫hstack，hstack的使用套路代码如下：

import numpy as np

a = np.array([[8, 8], [0, 0]])
b = np.array([[1, 8], [0, 4]])

'''
将a和b按元组中的顺序横向拼接
结果为：[[8, 8, 1, 8],
[0, 0, 0, 4]]
'''
print(np.hstack((a,b)))

c = np.array([[1, 2], [3, 4]])

'''
将a,b,c按元组中的顺序横向拼接
结果为：[[8, 8, 1, 8, 1, 2],
[0, 0, 0, 4, 3, 4]]
'''
print(np.hstack((a,b,c)))

(2)vstack

你还是某公司的HR，你记录了公司员工的一些信息，如下：

工号	姓名	出生年月	联系电话
1	张三	1988.12	13323332333
2	李四	1987.2	15966666666
3	王五	1990.1	13777777777
4	周六	1996.4	13069699696

今天有两位新同事入职，你需要记录他们的信息，如下：

工号	姓名	出生年月	联系电话
5	刘七	1986.5	13323332331
6	胡八	1997.3	15966696669

然后你需要将新入职同事的信息和已经入职的员工信息整合在一起。

工号	姓名	出生年月	联系电话
1	张三	1988.12	13323332333
2	李四	1987.2	15966666666
3	王五	1990.1	13777777777
4	周六	1996.4	13069699696
5	刘七	1986.5	13323332331
6	胡八	1997.3	15966696669

在这种情况下，你在整合的时候是将两个表格（二维数组）在竖直方向上堆叠在一起组合起来，拼接成一个新的表格（二维数组）。像这种行为称之为vstack（vertical stack）。

NumPy提供了实现vstack功能的函数叫vstack，vstack的使用套路代码如下：

    import numpy as np
    a = np.array([[8, 8], [0, 0]])
    b = np.array([[1, 8], [0, 4]])
    '''
    将a和b按元组中的顺序纵向拼接
    结果为：[[8, 8]
            [0, 0]
            [1, 8]
            [0, 4]]
    '''
    print(np.vstack((a,b)))
    c = np.array([[1, 2], [3, 4]])
    '''
    将a,b,c按元组中的顺序纵向拼接
    结果为：[[8 8]
            [0 0]
            [1 8]
            [0 4]
            [1 2]
            [3 4]]
    '''
    print(np.vstack((a,b,c)))

(3)尝试

测试用例输入是一个字典，feature1部分代表函数中的feature1，feature2部分代表函数中的feature2。

测试输入： {'feature1':[[1, 2, 3, 4], [4, 3, 2, 1], [2, 3, 4, 5]], 'feature2':[[1], [2], [3]]}

预期输出： [2.33333333 2.66666667 3. 3.33333333 2. ]

import numpy as np


def get_mean(feature1, feature2):
    '''
    将feature1和feature2横向拼接，然后统计拼接后的ndarray中每列的均值
    :param feature1:待`hstack`的`ndarray`
    :param feature2:待`hstack`的`ndarray`
    :return:类型为`ndarray`，其中的值`hstack`后每列的均值
    '''
    #********* Begin *********#
    a=np.hstack((feature1,feature2))
    return np.mean(a, axis=0)#沿着a对象的0轴求均值
    #********* End *********#

---

二、比较、掩码和布尔逻辑

（1）比较

用 布尔掩码 来查看和操作数组中的值。和算术运算符一样，比较运算符在numpy中也是通过通用函数来实现的。比较运算符和其对应的通用函数如下：

比较运算符	通用函数
==	np.equal
!=	np.not_equal
<	np.less
<=	np.less_equal
>	np.greater
>=	np.greater_equal

这些比较运算符通用函数可以用于任意形状、大小的数组。示例如下：

data=np.array([('Alice', 4, 40),('Bob', 11, 85.5),('Cathy', 7, 68.0),('Doug', 9, 60)],dtype=[("name","S10"),("age","int"),("score","float")]) #构造结构化数组


print(data["age"]<10)
'''
输出：array([ True, False, True, True])
'''

print(data["score"]>60)
'''
输出:array([False, True, True, False])
'''

print(data["score"]>=60)
'''
输出:array([False, True, True, True])
'''

print(data["score"]<=60)
'''
输出:array([ True, False, False, True])
'''

print(data["age"]!=9)
'''
输出:array([ True, True, True, False])
'''

print((data["age"]/2)==(np.sqrt(data["age"])))
'''
输出:array([ True, False, False, False])
'''

（2）布尔数组作掩码

一种更加强大的模式是使用布尔数组作为掩码，通过该掩码选择数据的子数据集，实现一些操作：

data=np.array([('Alice', 4, 40), ('Bob', 11, 85.5) ,('Cathy', 7, 68.0),('Doug', 9, 60)],dtype=[("name","S10"),("age","int"),("score","float")])

print(data)
'''
输出：[(b'Alice', 4, 40. )
(b'Bob', 11, 85.5)
(b'Cathy', 7, 68. )
(b'Doug', 9, 60. )]
'''


print(data["score"]>60) #使用比较运算得的一个布尔数组
'''
输出:[False True True False]
'''

print(data[data["score"]>60]) #进行简单的索引，即掩码操作将值为True的选出
'''
输出:[(b'Bob', 11, 85.5) (b'Cathy', 7, 68. )]
'''

（3）布尔逻辑

结合Python的逐位逻辑运算符一起使用。逻辑运算符对应numpy中的通用函数如下表：

逻辑运算符	通用函数
&	np.bitwise_and
|	np.bitwise_or
^	np.bitwise_xor
~	np.bitwise_not

print(np.count_nonzero(data["age"]<10))#统计数组中True的个数
'''
输出:3
'''

#还可以用np.sum(),输出结果和count_nonzero一样,sum()的好处是可以沿着行或列进行求和
print(np.sum(data["age"]<10))

print(np.any(data["score"]<60))#是否有不及格的
'''
输出：True
'''

print(np.all(data["age"]>10))#是否都大于10岁
'''
输出:False
'''

print(data[data["age"]>10])#打印年龄大于10的信息
'''
输出：array([(b'Bob', 11, 85.5)],
dtype=[('name', 'S10'), ('age', '

（4）尝试

测试输入： [[ 3 ,15, 9 ,11 , 7],[ 2, 0 , 8, 19 ,16],[ 6 , 6, 16 , 9, 5],[ 7 , 5 , 2 , 6 ,13]] 10

预期输出： [15 11 19 16 16 13]

import numpy as np


def student(num,input_data):
    result=[]
    # ********* Begin *********#

    result=np.array(input_data)#实例化数组
    result=result[result>num]#将数组中大于num的元素放入result的数组中

    # ********* End *********#
    return result

---

三、花式索引与布尔索引

（1）花式索引

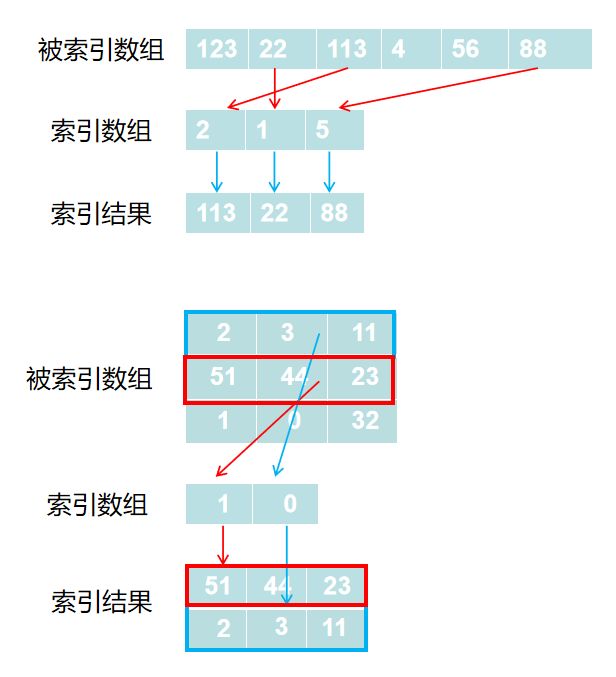
花式索引（Fancy Indexing）是NumPy用来描述使用整型数组（这里的数组，可以是NumPy的数组，也可以是python自带的list）作为索引的术语，其意义是根据索引数组的值作为目标数组的某个轴的下标来取值。

使用一维整型数组作为索引，如果被索引数组(ndarray)是一维数组，那么索引的结果就是对应位置的元素；如果被索引数组(ndarray)是二维数组，那么就是对应下标的行。如下图所示：

示例代码如下：

import numpy as np

arr = np.array(['zero','one','two','three','four'])

'''
打印arr中索引为1和4的元素
结果为：['one', 'four']
'''
print(arr[[1,4]])

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

'''
打印arr中索引为1和0的行
结果为：[[4, 5, 6],
[1, 2, 3]]
'''
print(arr[[1, 0]])

'''
打印arr中第2行第1列与第3行第2列的元素
结果为：[4, 8]
'''
print(arr[[1, 2], [0, 1]])

 （2）布尔索引

我们可以通过一个布尔数组来索引目标数组，以此找出与布尔数组中值为True的对应的目标数组中的数据，从而达到筛选出想要的数据的功能。如下图所示：（PS：需要注意的是，布尔数组的长度必须与被索引数组对应的轴的长度一致）

我们可以想办法根据我们的需求，构造出布尔数组，然后再通过布尔索引来实现筛选数据的功能。

假设有公司员工绩效指数的数据如下（用一个一维的ndarray表示），现在想要把绩效指数大于3.5的筛选出来进行股权激励。

那首先就要构造出布尔数组，构造布尔数组很简单，performance > 3.5即可。此时会生成想要的布尔数组。

有了布尔数组就可以使用布尔索引来实现筛选数据的功能了。

示例代码如下：

import numpy as np

performance = np.array([3.25, 3.5, 3.75, 3.5, 3.25, 3.75])

'''
筛选出绩效高于3.5的数据
结果为:[3.75, 3.75]
'''
print(performance[performance > 3.5])

'''
筛选出绩效高于3.25并且低于4的数据
注意：&表示并且的意思，可以看成是and。&左右两边必须加上()
结果为:[3.5 3.75 3.5 3.75]
'''
print(performance[(performance > 3.25) & (performance < 4)])

（3）尝试

测试输入： ["d","a","A","p","b","I","C","K"]

预期输出： ['A' 'I' 'C' 'K']

import numpy as np

def student(input_data):
    result=[]
    #********* Begin *********#
    result=np.array(input_data)
    result=result[(result>='A') & (result<='Z')]#输出A~Z的字符

    # ********* End *********#
    return result

四、广播机制

（1）广播

当两个ndarray对象的形状并不相同的时候，我们可以通过扩展数组的方法来实现相加、相减、相乘等操作，这种机制叫做广播（broadcasting）。

比如，一个二维的ndarray对象减去列平均值，来对数组的每一列进行取均值化处理：

import numpy as np

# arr为4行3列的ndarray对象
arr = np.random.randn(4,3)
# arr_mean为有3个元素的一维ndarray对象
arr_mean = arr.mean(axis=0)
# 对arr的每一列进行
demeaned = arr - arr_mean

很明显上面代码中的arr和arr_mean维度并不形同，但是它们可以进行相减操作，这就是通过广播机制来实现的。

（2）广播的原则

如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为1，则认为它们是广播兼容的。广播会在缺失或长度为1的维度上进行，这句话是理解广播的核心。

广播主要发生在两种情况，一种是两个数组的维数不相等，但是它们的后缘维度的轴长相符，另外一种是有一方的长度为1。

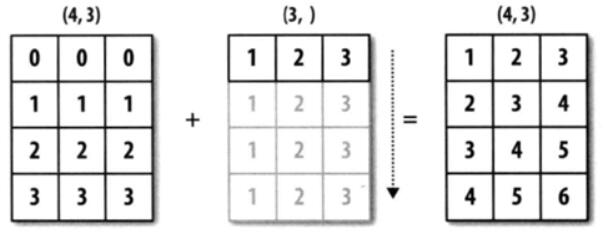
我们来看一个例子：

import numpy as np

arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]])
arr2 = np.array([1, 2, 3])
arr_sum = arr1 + arr2
print(arr_sum)

'''
输入结果如下:
[[1 2 3]
[2 3 4]
[3 4 5]
[4 5 6]]
'''

arr1的shape为(4,3)，arr2的shape为(3,)。可以说前者是二维的，而后者是一维的。但是它们的后缘维度相等，arr1的第二维长度为3，和arr2的维度相同。

arr1和arr2的shape并不一样，但是它们可以执行相加操作，这就是通过广播完成的，在这个例子当中是将arr2沿着0轴进行扩展。

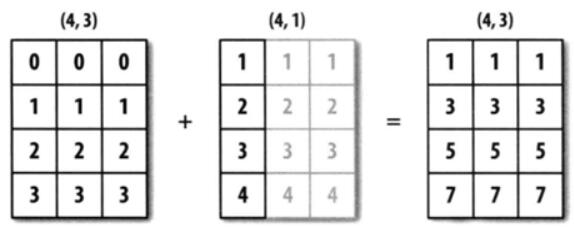
我们再看一个例子：

import numpy as np

arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]]) #arr1.shape = (4,3)
arr2 = np.array([[1],[2],[3],[4]]) #arr2.shape = (4, 1)

arr_sum = arr1 + arr2
print(arr_sum)

'''
输出结果如下：
[[1 1 1]
[3 3 3]
[5 5 5]
[7 7 7]]
'''

arr1的shape为(4,3)，arr2的shape为(4,1)，它们都是二维的，但是第二个数组在1轴上的长度为1，所以，可以在1轴上面进行广播。

（3）尝试

测试输入：

[[9, 3, 1], [7, 0, 6], [4, 6, 3]] [1, 5, 9] [[9], [6], [7]]

预期输出：

1. [[19 17 19]
2. [14 11 21]
3. [12 18 19]]

import numpy as np

def student(a,b,c):
    result=[]
    # ********* Begin *********#

    a=np.array(a)
    b=np.array(b)
    c=np.array(c)
    result=a+b+c


    # ********* End *********#
    return result

---

五、线性代数

（1）numpy的线性代数

常用的numpy.linalg函数：

函数	说明
dot	矩阵乘法
vdot	两个向量的点积
det	计算矩阵的行列式
inv	计算方阵的逆
svd	计算奇异值分解（SVD）
solve	解线性方程组 Ax=b，A是一个方阵
matmul	两个数组的矩阵积

1.dot()

该函数返回两个数组的点积。对于二维向量，效果等于矩阵的乘法；对于一维数组，它是向量的内积；对于N维数组，它是a的最后一个轴上的和与b的倒数第二个轴的乘积。（两个矩阵相乘，为行乘列）

 

    a=np.array([[1,2],[3,4]])
    a1=np.array([[5,6],[7,8]])
    np.dot(a,a1)
    '''
    输出：array([[19, 22],
           [43, 50]])
    '''

2.det()

用于计算输入矩阵的行列式

    a = np.array([[14, 1], [6, 2]])
    a=linalg.det(a)
    print(a)
    '''
    输出：21.999999999999996
    '''

3.inv()

用于计算方阵的逆矩阵。逆矩阵的定义维如果两个方阵A、B，使得AB = BA = E，则A称为可逆矩阵，B为A的逆矩阵，E为单位矩阵。

a=np.array([[1,2],[3,4]])

b=linalg.inv(a)

print(np.dot(a,b))
'''
输出：array([[1.0000000e+00, 0.0000000e+00],
[8.8817842e-16, 1.0000000e+00]])
'''

4.solve()

用于计算线性方程的解。

假设有如下方程组：3x+2y=7 x+4y=14；

写成矩阵的形式：[[3,2][1,4]]*[[x],[y]]=[[7],[14]]；

解如上方程组代码如下：

     a=np.array([[3,2], [1,4]])
     b=np.array([[7],[14]])
     linalg.solve(a,b)
    '''
     输出:array([[0. ],
           [3.5]])
     最后解出x=0，y=3.5
    '''

5.matmul()

返回两个数组的矩阵乘积。如果参数中有一维数组，则通过在其维度上附加1来提升为矩阵，并在乘法之后去除。

    a=[[3,4],[5,6]]
    b=[[7,8],[9,10]]
    np.matmul(a,b)
    '''
    输出：array([[ 57,  64],
           [ 89, 100]])
    '''
    b=[7,8]
    np.matmul(a,b)
    '''
    输出：array([53, 83])
    '''

6.svd()

奇异值分解是一种矩阵分解的方法，该函数用来求解SVD。

    a=[[0,1],[1,1],[1,0]]
    linalg.svd(a)
    '''
    输出:(array([[-4.08248290e-01,  7.07106781e-01,  5.77350269e-01],
           [-8.16496581e-01,  2.64811510e-17, -5.77350269e-01],
           [-4.08248290e-01, -7.07106781e-01,  5.77350269e-01]]), array([1.73205081, 1.        ]), array([[-0.70710678, -0.70710678],
           [-0.70710678,  0.70710678]]))
    '''

（2）尝试

测试输入：

[["男",2,4,40],["女",8,3,17],["男",8,6,24]]

预期输出：

1. [[-7.2]
2. [13.6]]

from numpy import linalg
import numpy as np
def student(input_data):
    '''
    将输入数据筛选性别为男，再进行线性方程求解
    :param input_data:类型为`list`的输入数据
    :return:类型为`ndarray`
    '''
    result=[]
    # ********* Begin *********#
    a=np.array(input_data)
    x=[]
    y=[]
    for i in a:#以数组a的长度来循环
        if i[0]=="男":#判断如果第一个元素是男"
            x.append([int(i[1]),int(i[2])])
            y.append([int(i[-1])])
    if x==[] and y==[]:
        return result
    x=np.array(x)
    y=np.array(y)
    result=linalg.solve(x,y)#解线性方程

    # ********* End *********#
    return result