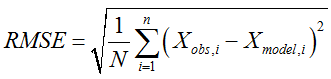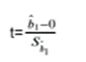线性回归及代码实现
引子
初等数学➡已知方程求未知数
高等数学→已知未知数,求方程(从数据中获得结论)
那么今天就从里面最简单的线性回归(Simple linear regression)开始学起
最简单的理解就是通过一些列运算的到初中我们学的y=kx+b
第一步,描述数据(数据可视化)
比如我们通过散点图看到整个数据,好像是接近一条线(类似于y=kx+b)那样分布的,我们就可以使用简单线性回归进行预测(图为探寻工作年限与薪水的关系)

这里先引入协方差(covariance)的概念
作用:描述多维数据集(标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集)
原理:计算两组数据的平均值之间的数据的差距(距离),再把它们的差距进行相乘,以此达到寻求两组数据之间的联系的目的(Linear correlation)
公式:

这里面除的不是n而是n-1的问题详见贝塞尔矫正推导那篇博文
拓展:
与期望的联系

缺陷:只能反应数据是否同向变动(正则同向,负则反向变动)因为当两个数据差距很大比如100与10000它们乘起来数值也会很大,不能说数值越大就代表关联越强
于是,我们这时需要一个新的工具来衡量多维数据之间的联系,这就是相关性,这里我们讨论皮尔逊相关性
这里部分内容源自百度百科
定义:
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商
公式:

上式定义了总体相关系数,常用希腊小写字母作为代表符号。估算样本的协方差和标准差,可得到皮尔逊相关系数,常用英文小写字母 代表:
观察公式相比协方差,它引入了标准差,标准差公式(后续我会发标准差公式的博文)的意义在于借正态分布公式使得数值在0到1之间和表示事情发生的概率(数据离散程度,联想正态分布的那个图,离中间越远→概率越小→该数据离散)从而达到数据归一化的同时表示数据之间的联系的目的.
为方便说明,我们先假定我们已经有一个模型,y=kx+b,预测值为y1,实际值为ya
这里再明确一个概念,残差
简单来说就是预测值与实际值直接的差值(距离)
即y1-ya
那么模型准确度的评估的方法就是让所有线上的点的残差加起来最小
但是要注意,这个残差的正负不确定,所有不能单纯地对残差进行相加(一般我们不用绝对值,因为这个计算机制要分类讨论会增加电脑的负担,一般直接平方,且分段函数无法求导)
结果越小,拟合效果越好
用python语言就是
E = min(sum((y1-ya)**2))/n(n代表一共有几组数据)→最小二乘法(oridinary least square有时也简称为ols)
回归方程的系数的确定
这里假定我们要求的函数为y=b0+b1x
那么相关系数计算公式就是:
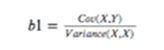 即协方差/方差
即协方差/方差
把公式套进去就会发现改相关性系数其实就是上面的E即残差的和即预测值与实际值直接的差值(距离)
这个距离的和越小→预测值与实际值的距离越小→改线就越能接近实际值的点→拟合效果越好
part2ANOVA
ANOVA(方差分析(Analysis of Variance,简称ANOVA))
目的:用于表达我们的模型有多拟合数据
就是一张表

关于这类表,有个推论:TSS = SSE + RSS
其中,回归平方和:ESS,残差平方和:RSS,总体平方和:TSS。
即总体平方和=回归平方和+误差平方和(总体=预测+误差)
参数说明:
(1) 实验条件,即不同的处理造成的差异,称为组间差异。用变量在各组的均值与总均值之偏差平方和的总和表示,记作SSb,组间自由度dfb。
(2) 随机误差,如测量误差造成的差异或个体间的差异,称为组内差异,用变量在各组的均值与该组内变量值之偏差平方和的总和表示, 记作SSw,组内自由度dfw。
总偏差平方和 SSt = SSb + SSw。
组内SSw、组间SSb除以各自的自由度(组内dfw =n-m,组间dfb=m-1,其中n为样本总数,m为组数),得到其均方MSw和MSb,一种情况是处理没有作用,即各组样本均来自同一总体,MSb/MSw≈1。另一种情况是处理确实有作用,组间均方是由于误差与不同处理共同导致的结果,即各样本来自不同总体。那么,MSb>>MSw(远远大于)。
MSb/MSw比值构成F分布。用F值与其临界值比较,推断各样本是否来自相同的总体 。
R**2=残差平方和/总体平方和→用于表示模型的拟合度,数值越接近1代表得到的回归方程越好或越适合(模型拟合越好)

SSR即RSS,SST即TSS,其他同理
浅谈简单线性回归(Simple linear regression)part3SEE,MSE,SSE的关系
MSE→均方根误差(各数据偏离真实值 差值的平方和 的平均数 )→Meansquared erro
SEE→标准估计误差→standard estimated errors
目的:描述真实值与预测值之间的距离
SSE→和方差、误差平方和→The sum of squares dueto error
part3SEE,MSE,SSE的关系
MSE→均方根误差(各数据偏离真实值 差值的平方和 的平均数 )→Meansquared erro
SEE→标准估计误差→standard estimated errors
目的:描述真实值与预测值之间的距离
SSE→和方差、误差平方和→The sum of squares dueto error
part4对参数检验的两种方式
1point_estimation(点估计)→一般被认为不太科学(就是点对点,只有模型的参数完全符合该值我们才认为模型是准的),就是part1中讲的从一堆的点数据中得出的b1参数
2confidence interval(置信区间)→认为真实的b1是一个波动值,在一定的区间范围内浮动(联想食品包装袋上的±号),如果我们模型跑出来的参数落在了该区间内,我们就认为该模型是准的,具体见假设性检验那篇博文
part5.假设检验2
假设检验2
1假设性检验
详见https://blog.csdn.net/CSDNXXCQ/article/details/113145468
因为是要拿来拟合的模型,我们当然希望系数b1不为0
故我们先设一个靶子
H0→b1=0
Ha→b1≠0
3看t值落在正态分布的哪个区间内,比如左边,右边还是中间
4得出结论
:b1 was significantly different from 0(b1与0显著性不同)→拒绝了H0假设
注意,不一定要与0进行判断,这里只是判断b1与0是否相关.
接下来推广到多元的情况(联合检验/F检验)
假定现在有个方程y=b0+b1x1+b2x2+b3x3+…+bkxk
如果挨个检验,那么从b1到bk每个系数都能单独为0.显然这样有点不科学
故现在引入F检验
步骤基本差不多
H0→b1=b2=b3=…=bk=0
Ha→至少有一个bi≠0
观察该公式→RSS相比于SSE,越大→回归的斜率越大→至少有一个bi≠0
→越能拒绝该假设→联想正态分布的那张图,这是个单尾检验
原理推导:
https://wenku.baidu.com/view/5b1761a5551810a6f524866d.html
part6,离群点的处理
同时做两种方案,
1去除离群点
2保留离群点
然后对比两种方案的拟合效果
part7,伪相关
1,凑巧相关(chance relationship)→某一段时期内凑巧具有相关性
2,不是具有直接的相关性(not direct relation)→两个变量的关联由另外一个变量引起
这里面分为两种情况1,x,y里面包含了第三变量,2x,y同时与第三个变量相关但是他们之间没有关联
part8.从本源理解线性回归算法
回归分析法是非常常见的算法
本质:通过模型抓住信息拟合数据从而达到预测的目的
抓一个信息→简单线性回归(一元)→y=kx+b
抓住多个信息→多元线性回归→y=b0+k1x1+k2x2+…+knxn
但是由此就产生了一个问题,在日常生活中,我们观测到的数据不存在可以使用的通用的能完美拟合所有数据的算法,故我们只能尽力缩小该算法拟合数据的误差,于是为了尽可能地接近我们想计算的数据区间,我们想到了最小二乘法.
现在我们把目光转向矩阵,目的在于拟合数据(x1,y1)…(xn,yn)
下面把数据分别放入y=kx+b中,结合矩阵的性质进行变换(理解起来需要点线代基础)
#变换之后的A就用到了最小二乘法.

对于上面A的理解,注意,矩阵是可以转换成向量的,那么就能用向量去理解,该式子的目的在于在空间(3维)上使用向量对目标向量A尽可能地拟合.
part9 OLS算法的多种实现形式(附代码)
import numpy as np
import statsmodels.api as sm
#涉及的原理见https://blog.csdn.net/CSDNXXCQ/article/details/113810988
num_simple = 101
x = np.linspace(0,10,num_simple)#x = np.linspace(0, 1, 500)#创建一个0~1的随机数组,元素设定为500个
#约定俗成再对x进行变换后要大写
X = sm.add_constant(x)#自动在增加一个全为1的列在第一列
beta = np.array([1,10])
#残差一般是一个正态分布,故我们这里通过正态分布将其表现出来
e = np.random.normal(size=num_simple)#详见https://blog.csdn.net/CSDNXXCQ/article/details/113819123
y = np.dot(X,beta)+e#参考https://blog.csdn.net/CSDNXXCQ/article/details/113819212
#现在反求beta
#方法一
B = np.dot(np.dot(np.linalg.inv(np.dot(X.T,X)),X.T),y)#这样解很容易弄晕,一般不推荐这样写#np.linalg.inv():矩阵求逆
print('现在对比下我们刚刚设定的beta值:{}与{}'.format(beta,B))
#方法二
#直接使用三个矩阵连乘,比如现在有矩阵ABC我们要连乘可以这样:A.doy(B).dot(B)
B = np.linalg.inv(np.dot(X.T,X)).dot(X.T).dot(y)
print('现在对比下我们刚刚设定的beta值:{}与{}'.format(beta,B))
#方法三,调库
model = sm.OLS(y,X)#通过OLS方法(最小二乘法)去拟合X,y数据
result = model.fit()
B = result.params#输出拟合的参数
print('现在对比下我们刚刚设定的beta值:{}与{}'.format(beta,B))
print(result.summary())#显示各种详细参数
线性回归代码实现
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
# 模型评价
# MSE, RMES, R-square
from sklearn import metrics
rng = np.random.RandomState(1)
xtrain = 10 * rng.rand(30)#创建随机数
ytrain = 15 + 4 * xtrain + rng.rand(30) * 3
# 创建数据
model = LinearRegression()
model.fit(xtrain[:,np.newaxis],ytrain)
ytest = model.predict(xtrain[:,np.newaxis])
mse = metrics.mean_squared_error(ytrain,ytest)
rmse = np.sqrt(mse)# 求出均方根
#ssr = ((ytest - ytrain.mean())**2).sum()
#sst = ((ytrain - ytrain.mean())**2).sum()
#r2 = ssr / sst # 求出确定系数
r2 = model.score(xtrain[:,np.newaxis],ytrain)
print("均方差MSE为: %.5f" % mse)
print("均方根RMSE为: %.5f" % rmse)
print("确定系数R-square为: %.5f" % r2)