【数据结构与算法】| 二叉树

一、树形结构

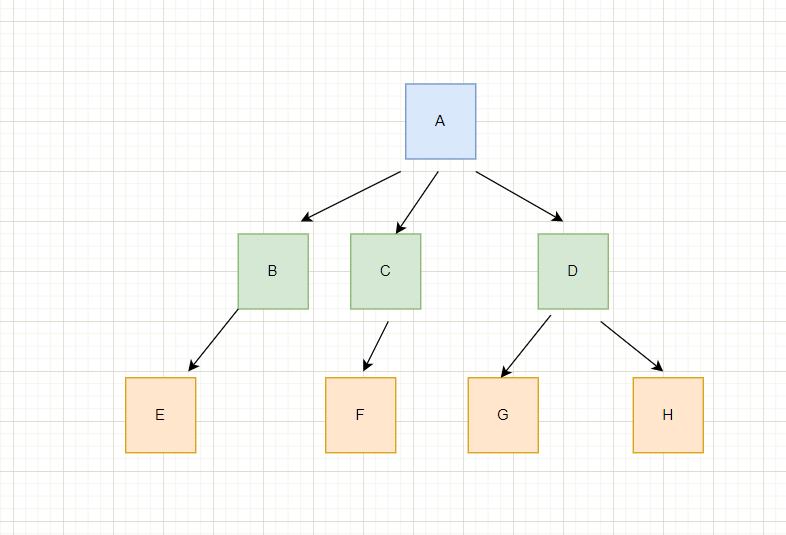
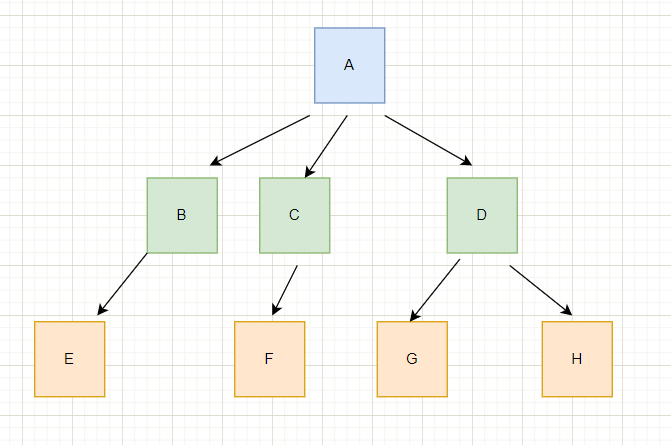
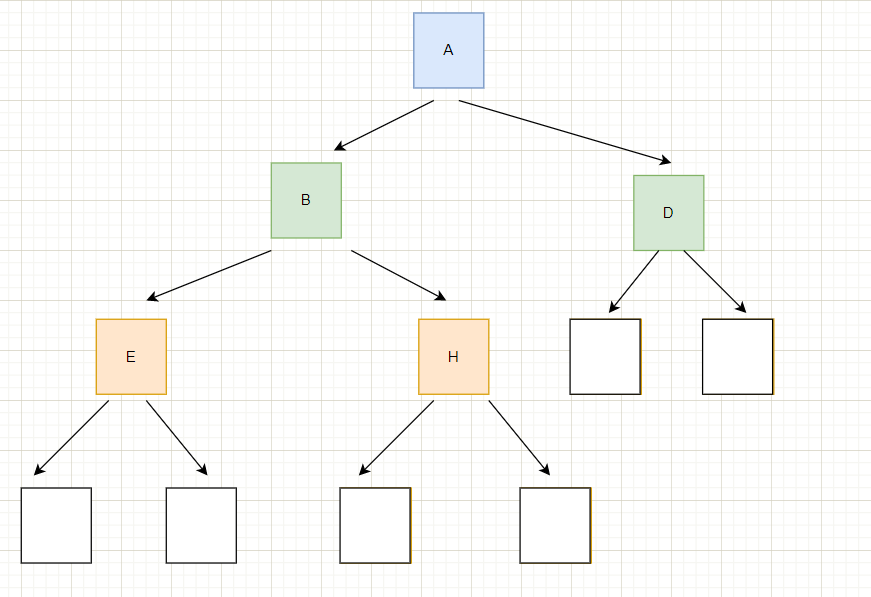
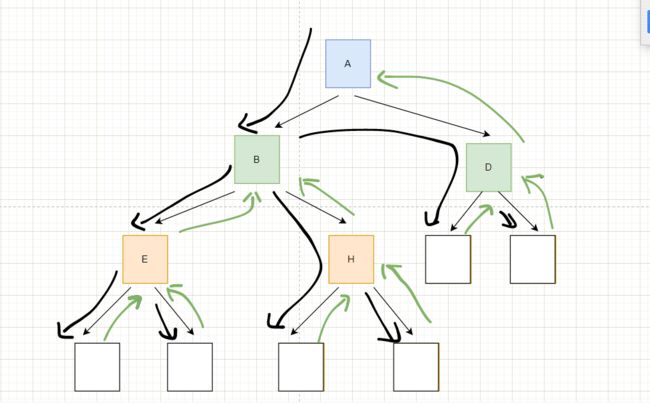
图示：

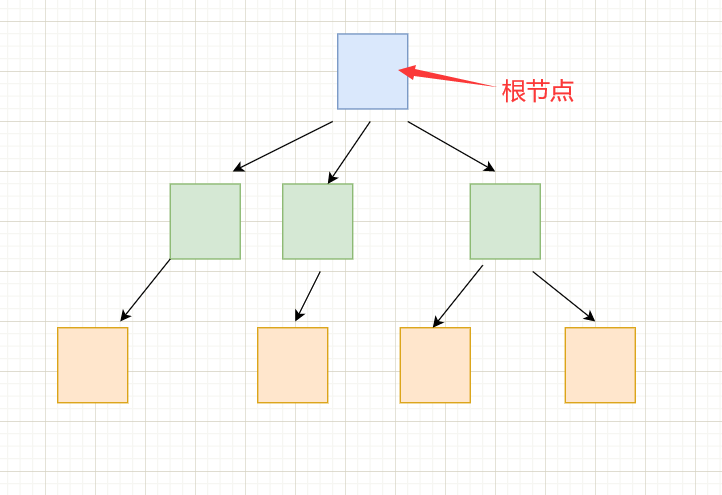
根节点

在上面的图中，蓝色的节点是没有前驱节点的，就代表着是根节点。其他有前驱节点的称为节点

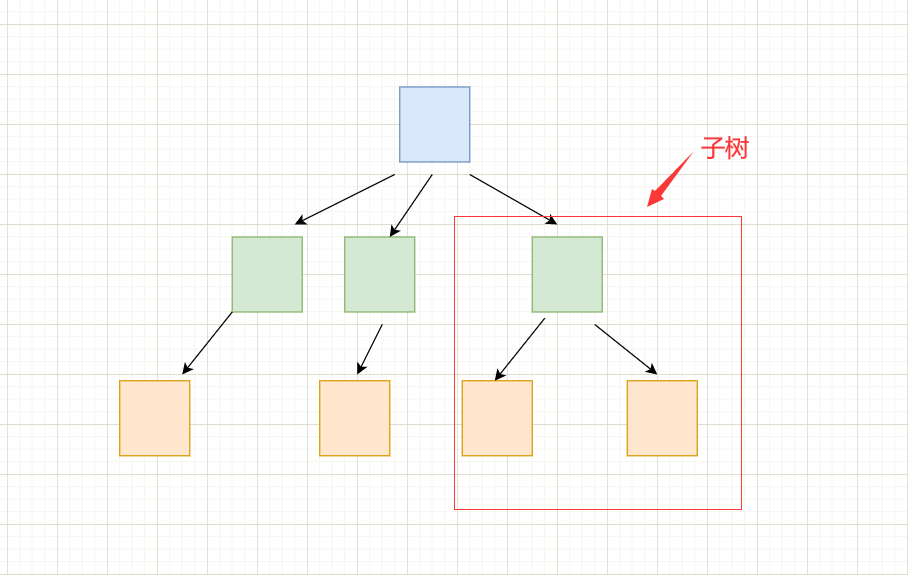
子树

除了根节点以外，其他节点也可以作为一棵树，这棵树就叫做子树。

注意！！！ 根节点只有一个，其他节点可以有多个也可以没有。

另外，子树与子树之间是不能有交集的，否则就不能是树形结构了。

树的概念

度

一个节点含有子节点的个数称之为度。就好比一个人有多少个孩子。

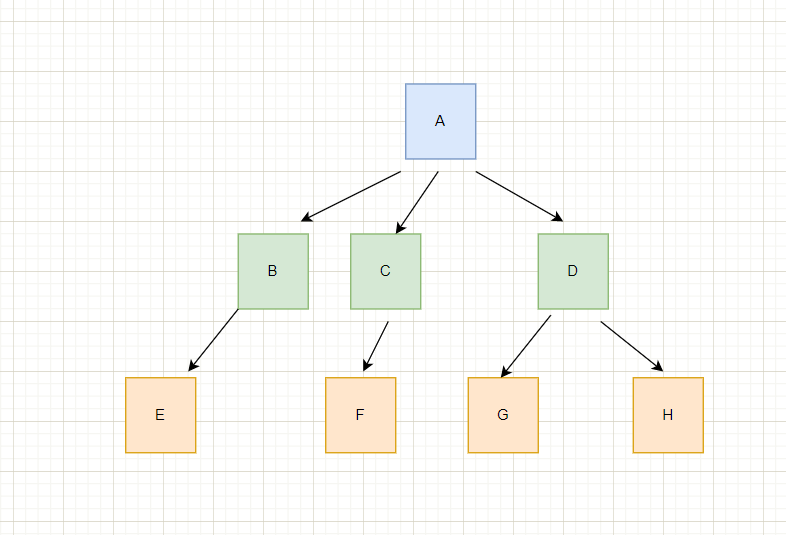
例如A的度是3。

树的度

树的度是指整棵树中最大的度，我的理解就是家里面每个儿子谁孩子最多。

如上图，树的度为3。

叶子节点或者终端节点

叶子节点就是所谓的度为0的节点，就是家里面暂时还没有孩子的人，就是类似一棵树中的叶子。

如上图，EFGH都是叶子节点

父节点

如果该节点含有子节点，那么该节点就是父节点。就好比一个人如果有了孩子，那么这个人都可以当爸爸了。

如上图，C是F的父节点。

孩子节点或子节点

如果一个节点含有父节点，那么该节点就成为子节点。就好比一个人有了爸爸，那么他就是个孩子啦。

如上图，E是B的孩子节点。

节点的层次

以根节点为基准，根节点是第一层，以此往下推。就类似楼层的高度，都是相对于第一层来说的。

如上图，G的层次是3。

树的高度

树中节点的最大层次。就是这棵树有多高。

该树的高度为3

二叉树

二叉树用我自己的理解就是每一棵树的度都只能小于等于2。

这是一颗二叉树

这也是一颗二叉树

二叉树

注意！！！二叉树的子树是有左右之分的，不能颠倒。因此二叉树是有序树。

二叉树的遍历方式

前序遍历

他的遍历顺序是 根 -> 左子树 - > 右子树。

例题

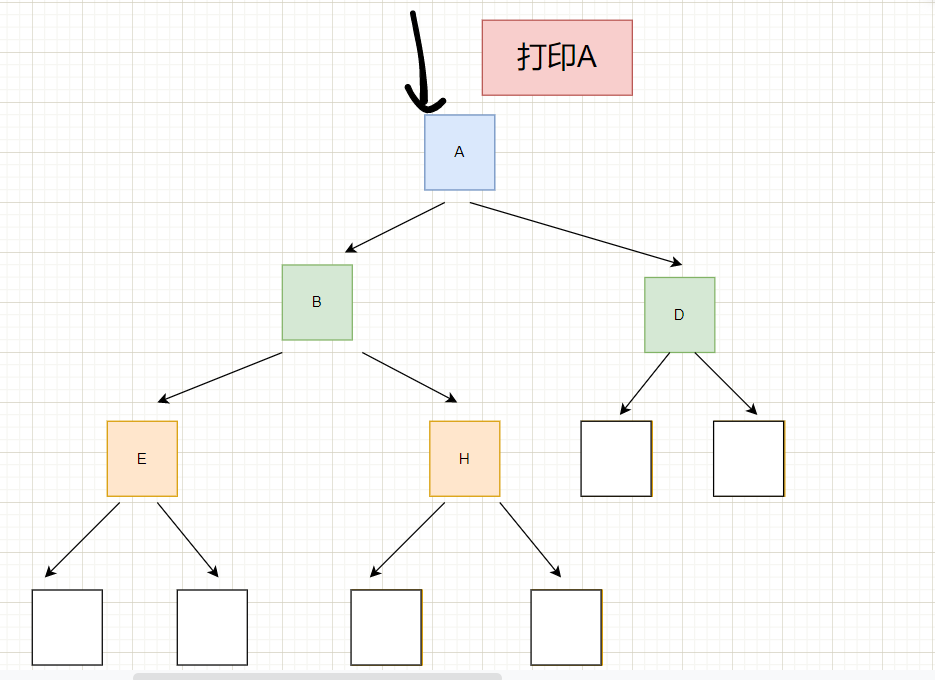
先从根节点开始，碰到根节点就处理，例如我这里是打印，那么我就先打印A,然后走到左节点B，B也是根节点，所以打印B，然后走到左节点E，是根节点就打印E，然后E的左节点是空，那么就返回到B，然后走右节点H，然后打印，H的左节点为空，返回到H走到H的右节点，为空，然后返回到H，返回B，返回A，走到A的右节点D，D也是根节点，打印D，然后走到D的左节点，左节点为空，然后返回D，走到D的右节点，右节点也为空，返回D，返回A，最后结束。

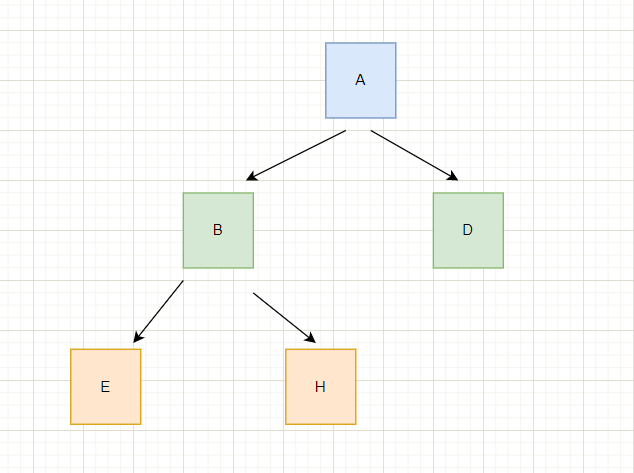
图示讲解，为了方便讲解，我把空节点都给显示了出来。

先从根节点A开始走，根据根 -> 左子树 - > 右子树的规则，所以打印A

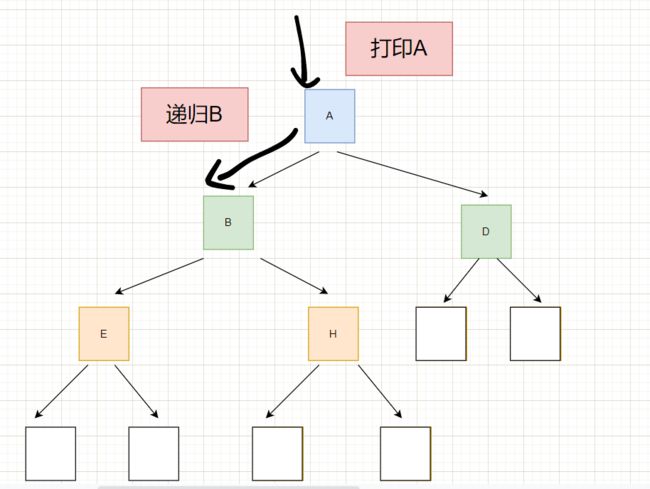
然后走到A的左节点，就是B，B也是根节点，这里的根节点不是整棵树的根节点，而是B的这棵子树的根节点。

所以B是根节点，所以打印。

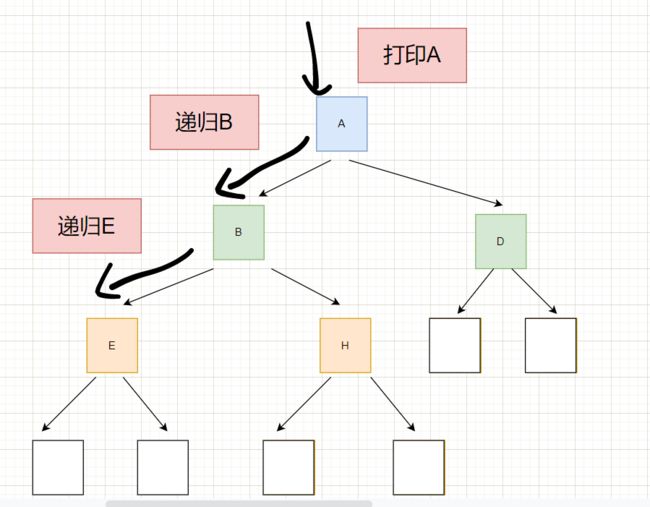
然后再走到B的左节点E，E也是根节点，所以打印E

然后走到E的左节点，左节点为空，然后回退到E

然后再走到E的右节点，右节点为空，然后回退到E，E再回退到B

然后走到B的右节点H，H是根节点，那么就打印。

然后重复以上步骤，接下来省略一万字。。。

所以打印的序列是ABEHD

中序遍历

中序遍历的规则是：左子树 - > 根节点 - > 右子树

所以打印的顺序是EBHAD

后续遍历

规则：左子树 -> 右子树 - > 根节点

打印的顺序是：EHBDA

关于二叉树学习的小结

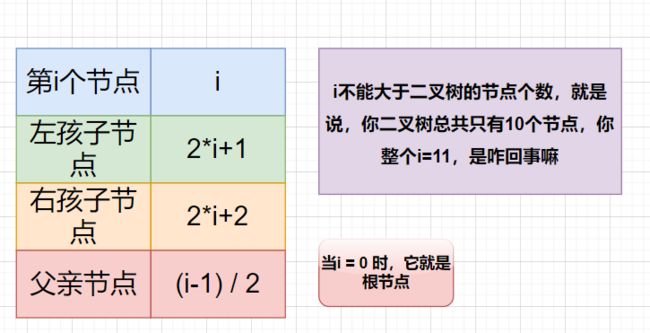
1.根节点和孩子节点

如果给你一个节点i，那么它的左孩子节点就是（2*i +1），右孩子节点就是(2*i+2).但是前提是这个数不能大于二叉树的节点个数。

给你一个节点，让你求父亲节点，那么就是（i-1）/ 2。

2.递归

关于二叉树的题，都是一些递归问题，还有就是借助其他数据结构来辅助解题。

经典的递归

1.前序遍历

2.中序遍历

3.后序遍历

其他数据结构辅助

1.打印每一层的节点

2.三种遍历的非递归版本