二叉树—98.验证二叉搜索树 108.将有序数组转换为二叉搜索树 101. 对称二叉树 235. 二叉搜索树的最近公共祖先 236. 二叉树的最近公共祖先 C++实现
文章目录
- 98.验证二叉搜索树
-
- 方法1 DFS 递归法+数组
- 方法2 DFS 递归法
- 方法3 BFS 迭代法
- 108.将有序数组转换为二叉搜索树
-
- 方法1 DFS 递归法
- 方法2 BFS 迭代法
- 101. 对称二叉树
-
- 方法1 DFS 递归法
- 方法2 BFS 迭代法
- 235. 二叉搜索树的最近公共祖先
-
- 方法1 DFS 递归法
- 方法2 BFS 迭代法
- 236. 二叉树的最近公共祖先
- 相关题目的二叉树总结点
98.验证二叉搜索树
方法1 DFS 递归法+数组
转成有序数组判断
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isValidBST(TreeNode* root) {
//1.方法一 转成有序数组
vec.clear();
dfs(root);
//判断数组是否有序
for(int i=1; i<vec.size(); i++)
{
if(vec[i] <= vec[i-1]) return false;
}
return true;
}
private:
//二叉树转数组
vector<int> vec;
void dfs(TreeNode* cur)
{
if(cur == nullptr) return;
dfs(cur->left);
vec.push_back(cur->val);
dfs(cur->right);
}
};
方法2 DFS 递归法
不使用数组
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isValidBST(TreeNode* root) {
//2.方法二 不使用数组
if(root == nullptr) return true;
bool left = isValidBST(root->left);
if(maxVal < root->val) maxVal = root->val;
else return false;
bool right = isValidBST(root->right);
return left && right;
}
private:
//2.方法二 不使用数组
long long maxVal = LONG_MIN;
};
方法3 BFS 迭代法
用栈模拟,中序模拟
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isValidBST(TreeNode* root) {
//3.方法三 迭代法
//中序遍历入栈 出栈时右中左顺序 栈顶元素cur小于栈顶下一个元素pre 说明不是搜索树
stack<TreeNode*> st;
if(root != nullptr) st;
TreeNode* cur = root;
TreeNode* pre = NULL;//记录前一个节点
while(cur != nullptr || !st.empty())
{
if(cur != nullptr)
{
st.push(cur);
cur = cur->left;//左节点
}
else
{
cur = st.top();//中节点
st.pop();
if(pre != nullptr && cur->val <= pre->val) return false;
pre = cur;//记录前一个节点
cur = cur->right;//右节点
}
}
return true;
}
};
108.将有序数组转换为二叉搜索树
将有序数组以数组中间位置的节点进行分割左右区间,分别作为左右子树。
方法1 DFS 递归法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
//方法1 DFS 递归 左闭右闭区间
return dfs(nums, 0, nums.size()-1);
}
private:
TreeNode* dfs(vector<int>& nums, int start, int end)
{
if(start > end) return nullptr;
//如果数组是偶数长度 相当于根节点取中间靠左的值
int mid = start + ((end - start) / 2);//根节点坐标
TreeNode* root = new TreeNode(nums[mid]);
root->left = dfs(nums, start, mid - 1);
root->right = dfs(nums, mid + 1, end);
return root;
}
};
方法2 BFS 迭代法
三个队列模拟,一个存放遍历的节点,一个存放左区间下标,一个存放右区间下标
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
//方法2 BFS 迭代法
if(nums.size() == 0) return nullptr;
TreeNode* root = new TreeNode(0);// 初始根节点
queue<TreeNode*> quelist;// 放遍历的节点
queue<int> queleft;// 保存左区间下标
queue<int> queright;// 保存右区间下标
quelist.push(root);// 根节点入队列
queleft.push(0);// 0为左区间下标初始位置
queright.push(nums.size() - 1);// nums.size() - 1为右区间下标初始位置
while(!quelist.empty())
{
TreeNode* cur = quelist.front(); quelist.pop();
int left = queleft.front(); queleft.pop();
int right = queright.front(); queright.pop();
int mid = left + ((right - left) / 2);
cur->val = nums[mid];//中节点
if(left <= mid - 1)//左节点
{
cur->left = new TreeNode(0);
quelist.push(cur->left);
queleft.push(left);
queright.push(mid - 1);
}
if(right >= mid + 1)//右节点
{
cur->right = new TreeNode(0);
quelist.push(cur->right);
queleft.push(mid + 1);
queright.push(right);
}
}
return root;
}
};
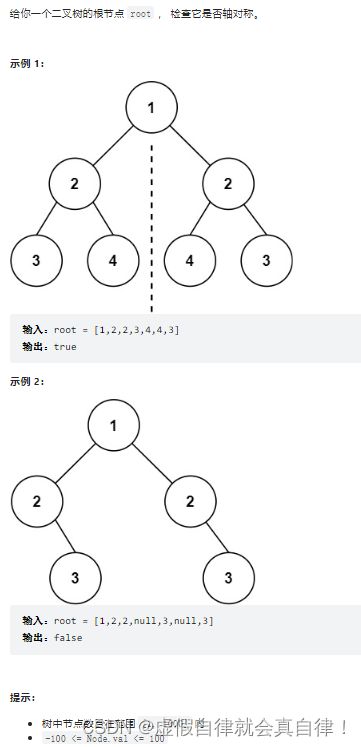
101. 对称二叉树
比较左右子树,需要考虑四种情况
- 左右节点都空
- 左节点为空 右节点不空 或者 左节点不空 右节点空
- 左右节点都不空 节点值不相同
- 左右节点不空且数值相等
方法1 DFS 递归法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
//方法1 dfs 后序遍历
if(root == nullptr) return true;
return dfs(root->left, root->right);
}
private:
//方法1 dfs 后序遍历
bool dfs(TreeNode* left, TreeNode* right)
{
//四种情况
//1.左右节点都空
//2.左节点为空 右节点不空 或者 2.左节点不空 右节点空
if(!left && !right) return true;
else if(!left || !right) return false;
//3.左右节点都不空 节点值不相同
else if(left->val != right->val) return false;
//4.左右节点不空且数值相等
//外侧节点相同 内侧节点相同
bool outsize = dfs(left->left, right->right);
bool inside = dfs(left->right, right->left);
return outsize && inside;//内外侧节点都相同才是对称树
}
};
方法2 BFS 迭代法
队列实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root == nullptr) return true;
//方法2 bfs 队列
queue<TreeNode*> que;
que.push(root->left);
que.push(root->right);
while(!que.empty())
{
TreeNode* leftcur = que.front(); que.pop();
TreeNode* rightcur = que.front(); que.pop();
if(!leftcur && !rightcur) return true;
if(!leftcur || !rightcur || leftcur->val != rightcur->val) return false;
que.push(leftcur->left);
que.push(rightcur->right);
que.push(leftcur->right);
que.push(rightcur->left);
}
return true;
}
};
栈实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root == nullptr) return true;
//方法2 bfs 栈
stack<TreeNode*> st;
st.push(root->left);
st.push(root->right);
while(!st.empty())
{
TreeNode* leftcur = st.top(); st.pop();
TreeNode* rightcur = st.top(); st.pop();
if(!leftcur && !rightcur) continue;
if(!leftcur || !rightcur || (leftcur->val != rightcur->val)) return false;
st.push(leftcur->left);
st.push(rightcur->right);
st.push(leftcur->right);
st.push(rightcur->left);
}
return true;
}
};
235. 二叉搜索树的最近公共祖先
利用二叉搜索树的有序性,三种情况
在[p->val, q->val]区间中
在[p->val, q->val]区间左边
在[p->val, q->val]区间右边
方法1 DFS 递归法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//方法1 DFS 递归法
return dfs(root, p, q);
}
private:
TreeNode* dfs(TreeNode* cur, TreeNode* p, TreeNode* q)
{
if(cur == nullptr) return cur;//中节点
if(cur->val > p->val && cur->val > q->val)//目标在左子树
{
TreeNode* left = dfs(cur->left, p, q);
if(left) return left;
}
if(cur->val < p->val && cur->val < q->val)
{
TreeNode* right = dfs(cur->right, p, q);
if(right) return right;
}
return cur;
}
};
方法2 BFS 迭代法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//方法2 BFS 迭代法
while(root)
{
if(root->val > p->val && root->val > q->val) root = root->left;
else if(root->val < p->val && root->val < q->val) root = root->right;
else return root;
}
return nullptr;
}
};
236. 二叉树的最近公共祖先
- 情况1:如果一个节点,左子树是节点p,右子树是节点q,或者左子树是节点q,右子树是节点p,那么该节点就是节点p和q的最近公共祖先
- 情况2:节点本身p(q),它拥有一个子孙节点q§,那么节点p(q)就是节点p和q的最近公共祖先
- 上述情况,相当于遇到 q 或者 p 就返回,返回值不为空,就说明找到了q或者p
- 遍历整棵树,从下往上遍历,后序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root || root==p || root==q) return root;
//后序遍历 遍历整棵树
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if(left && right) return root;//左右子树不为空 父节点就是最近祖先
else if(!left && right) return right;//左空 右不空 返回右
else if(left && !right) return left;//右空 左不空 返回左
return NULL;
}
};
相关题目的二叉树总结点
1. 二叉树遍历方式:
- 深度优先遍历DFS
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历BFS:层次遍历(迭代法)
2. 二叉树返回值:
递归函数什么时候需要返回值?什么时候不需要返回值?这里总结如下三点:
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值——113.路径总和Ⅱ
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值——236. 二叉树的最近公共祖先
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回——112. 路径总和
3. 二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
4. 二叉搜索树的应用: 与有序数组的转化、验证二叉搜索树、与平衡树的转化
5. 二叉平衡树的特征: 一棵二叉搜索树中,每个节点的两棵子树高度差不超过 1
6. 完美二叉树的特征 ——题116