[力扣刷题总结](双指针篇)
文章目录
- |||||||||||||||||||| 双指针 ||||||||||||||||||
- 905. 按奇偶排序数组
-
- 解法1:双指针+原地交换
- 解法2:两次遍历+保持相对位置
- 475. 供暖器
-
- 解法1:双指针+贪心
- 202. 快乐数
-
- 解法1:快慢指针
- 相似题目:141. 环形链表
-
- 解法1:快慢指针
- 相似题目:142. 环形链表 II
-
- 解法1:快慢指针
- 解法2:哈希表
- 相似题目:287. 寻找重复数
-
- 解法1:快慢指针
- 解法2:二分查找
- 15. 三数之和
-
- 解法1:双指针
- 相似题目:611. 有效三角形的个数
-
- 解法1:双指针
- 相似题目:16. 最接近的三数之和
-
- 解法1:双指针+排序
- 相似题目:1. 两数之和
-
- 解法1:哈希表
- 31. 下一个排列
-
- 解法1:两遍扫描+双指针
- 165. 比较版本号
-
- 解法1:双指针
- 75. 颜色分类
-
- 解法1:双指针+一次遍历
- 解法2:双指针+一次遍历
- ~~缩减搜索空间的思想~~
- 11. 盛最多水的容器
-
- 解法1:双指针
- 240. 搜索二维矩阵 II
-
- 解法1:双指针+二叉搜索树
- 167. 两数之和 II - 输入有序数组
-
- 解法1:双指针
- |||||||||||||||| 滑动窗口 ||||||||||||||||||
- 992. K 个不同整数的子数组
-
- 解法1:双指针(滑动窗口)
- 相似题目:904. 水果成篮
-
- 解法1:双指针(滑动窗口)
- 相似题目:76. 最小覆盖子串
-
- 解法1:滑动窗口
- 3. 无重复字符的最长子串
-
- 解法1:滑动窗口+哈希
- 424. 替换后的最长重复字符
-
- 解法1:滑动窗口
- 相似题目:485. 最大连续 1 的个数
-
- 解法1:数组+一次遍历
- 剑指 Offer 59 - I. 滑动窗口的最大值
-
- 解法1:滑动窗口+单调队列+双向队列
- 解法2:优先队列+滑动窗口
- 相似题目:剑指 Offer 59 - II. 队列的最大值
-
- 解法1:单调队列+滑动窗口
- 1052. 爱生气的书店老板
-
- 解法1:数组+滑动窗口
- 209. 长度最小的子数组
-
- 解法1:滑动窗口
- 相似题目:718. 最长重复子数组
-
- 解法1:动态规划
- 567. 字符串的排列
-
- 解法1:滑动窗口
|||||||||||||||||||| 双指针 ||||||||||||||||||
905. 按奇偶排序数组
力扣链接
给你一个整数数组 nums,将 nums 中的的所有偶数元素移动到数组的前面,后跟所有奇数元素。
返回满足此条件的 任一数组 作为答案。
示例 1:
输入:nums = [3,1,2,4]
输出:[2,4,3,1]
解释:[4,2,3,1]、[2,4,1,3] 和 [4,2,1,3] 也会被视作正确答案。
示例 2:
输入:nums = [0]
输出:[0]
提示:
1 <= nums.length <= 5000
0 <= nums[i] <= 5000
解法1:双指针+原地交换
class Solution {
public:
vector<int> sortArrayByParity(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
while (left < right) {
while (left < right and nums[left] % 2 == 0) {
left++;
}
while (left < right and nums[right] % 2 == 1) {
right--;
}
if (left < right) {
swap(nums[left++], nums[right--]);
}
}
return nums;
}
};
解法2:两次遍历+保持相对位置
class Solution {
public:
vector<int> sortArrayByParity(vector<int>& nums) {
vector<int> res;
for (auto & num : nums) {
if (num % 2 == 0) {
res.push_back(num);
}
}
for (auto & num : nums) {
if (num % 2 == 1) {
res.push_back(num);
}
}
return res;
}
};
475. 供暖器
力扣链接
冬季已经来临。 你的任务是设计一个有固定加热半径的供暖器向所有房屋供暖。
在加热器的加热半径范围内的每个房屋都可以获得供暖。
现在,给出位于一条水平线上的房屋 houses 和供暖器 heaters 的位置,请你找出并返回可以覆盖所有房屋的最小加热半径。
说明:所有供暖器都遵循你的半径标准,加热的半径也一样。
示例 1:
输入: houses = [1,2,3], heaters = [2]
输出: 1
解释: 仅在位置2上有一个供暖器。如果我们将加热半径设为1,那么所有房屋就都能得到供暖。
示例 2:
输入: houses = [1,2,3,4], heaters = [1,4]
输出: 1
解释: 在位置1, 4上有两个供暖器。我们需要将加热半径设为1,这样所有房屋就都能得到供暖。
示例 3:
输入:houses = [1,5], heaters = [2]
输出:3
提示:
1 <= houses.length, heaters.length <= 3 * 104
1 <= houses[i], heaters[i] <= 109
解法1:双指针+贪心
思路:
这是一道很好的贪心+双指针的应用题。
我们需要保证每个房屋至少在一个加热器的供暖范围内,那为了让加热半径最小,我们只需要保证每个房屋最近的加热器的距离小于加热半径。
那全局最低的加热半径;自然也就等于所有房屋到最近加热器的距离中的最大值。 这是一个min(max)的问题。
如果我们的房屋和加热器都是按照横坐标排序的;那显然,我们只需要顺次对每个房子找和他相邻的前后两个加热器即可。
用两个指针分别标记房屋和加热器;不断移动加热器,直至加热器的横坐标大于房屋横坐标。 则当前加热器指针 cur 和 cur-1 就是房屋左边的加热器和右边的加热器。
我们求两者到房屋距离中的较小值,就是该房屋最近的加热器到房屋的距离。
遍历所有的房屋,取最大值即可。
代码:
class Solution {
public:
int findRadius(vector<int>& houses, vector<int>& heaters) {
int result = 0;
sort(heaters.begin(),heaters.end());
sort(houses.begin(),houses.end());
int cur = 0;
for(int i = 0;i<houses.size();i++){
int curDis = abs(houses[i]-heaters[cur]);
while(cur < heaters.size()-1 && abs(houses[i]-heaters[cur+1]) <= curDis){
curDis = min(abs(houses[i]-heaters[cur+1]),curDis);
cur++;
}
result = max(result,curDis);
}
return result;
}
};
202. 快乐数
力扣链接
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
提示:
1 <= n <= 231 - 1
解法1:快慢指针
思路:
(1)使用 “快慢指针” 思想,找出循环:“快指针” 每次走两步,“慢指针” 每次走一步,当二者相等时,即为一个循环周期。此时,判断是不是因为 1 引起的循环,是的话就是快乐数,否则不是快乐数。
(2)这个算法是两个奔跑选手,一个跑的快,一个跑得慢。在龟兔赛跑的寓言中,跑的慢的称为 “乌龟”,跑得快的称为 “兔子”。
不管乌龟和兔子在循环中从哪里开始,它们最终都会相遇。这是因为兔子每走一步就向乌龟靠近一个节点(在它们的移动方向上)。
_第3张图片](http://img.e-com-net.com/image/info8/06166a772f534cc89d8e8982a387143c.jpg)
(3)注意:此题不建议用集合记录每次的计算结果来判断是否进入循环,因为这个集合可能大到无法存储;另外,也不建议使用递归,同理,如果递归层次较深,会直接导致调用栈崩溃。不要因为这个题目给出的整数是 int 型而投机取巧。
代码:
class Solution {
public:
int get_next(int n){
int sum = 0;
while(n>0){
sum += (n%10)*(n%10);
n /= 10;
}
return sum;
}
bool isHappy(int n) {
int slow = n, fast = n;
do{
slow = get_next(slow);
fast = get_next(fast);
fast = get_next(fast);
} while(slow != fast);//判断是否有循环
return slow == 1;
}
};
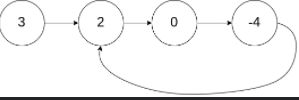
相似题目:141. 环形链表
力扣链接
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
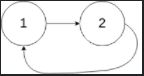
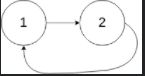
示例 2:
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
提示:
链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。
进阶:你能用 O(1)(即,常量)内存解决此问题吗?
解法1:快慢指针
参考
思路:
**当一个链表有环时,快慢指针都会陷入环中进行无限次移动,然后变成了追及问题。**想象一下在操场跑步的场景,只要一直跑下去,快的总会追上慢的。当两个指针都进入环后,每轮移动使得慢指针到快指针的距离增加一,同时快指针到慢指针的距离也减少一,只要一直移动下去,快指针总会追上慢指针。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode* slow = head, *fast = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
if (fast == slow) return true;
}
return false;
}
};
复杂度分析:
时间复杂度:O(N),其中 N 是链表中的节点数。
当链表中不存在环时,快指针将先于慢指针到达链表尾部,链表中每个节点至多被访问两次。
当链表中存在环时,每一轮移动后,快慢指针的距离将减小一。而初始距离为环的长度,因此至多移动 N轮。
空间复杂度:O(1)。我们只使用了两个指针的额外空间。
相似题目:142. 环形链表 II
力扣链接
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引
进阶:你是否可以使用 O(1) 空间解决此题?
解法1:快慢指针
思路:
这道题目,不仅考察对链表的操作,而且还需要一些数学运算。
主要考察两知识点:
1.判断链表是否环
2.如果有环,如何找到这个环的入口
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head, *slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
if(slow == fast){
ListNode* index = head;
while(index != slow){
index = index->next;
slow = slow->next;
}
return index;
}
}
return NULL;
}
};
复杂度分析:
时间复杂度:O(N),其中 N 为链表中节点的数目。在最初判断快慢指针是否相遇时,slow 指针走过的距离不会超过链表的总长度;随后寻找入环点时,走过的距离也不会超过链表的总长度。因此,总的执行时间为 O(N)+O(N)=O(N)。
空间复杂度:O(1)。我们只使用了slow,fast,ptr 三个指针。
解法2:哈希表
思路:
一个非常直观的思路是:我们遍历链表中的每个节点,并将它记录下来;一旦遇到了此前遍历过的节点,就可以判定链表中存在环。借助哈希表可以很方便地实现。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
unordered_map<ListNode*,int> umap;
ListNode* ptr = head;
while(ptr!=NULL){
if(umap[ptr] > 1) return ptr;
umap[ptr]++;
ptr = ptr->next;
}
return NULL;
}
};
复杂度分析:
时间复杂度:O(N),其中 N 为链表中节点的数目。我们恰好需要访问链表中的每一个节点。
空间复杂度:O(N),其中 N 为链表中节点的数目。我们需要将链表中的每个节点都保存在哈希表当中。
相似题目:287. 寻找重复数
力扣链接
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,找出 这个重复的数 。
你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
示例 3:
输入:nums = [1,1]
输出:1
示例 4:
输入:nums = [1,1,2]
输出:1
提示:
1 <= n <= 105
nums.length == n + 1
1 <= nums[i] <= n
nums 中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
进阶:
如何证明 nums 中至少存在一个重复的数字?
你可以设计一个线性级时间复杂度 O(n) 的解决方案吗?
解法1:快慢指针
代码:
class Solution {
public:
int findDuplicate(vector<int>& nums) {
//快慢指针
int slow = 0, fast = 0;
while(true){
slow = nums[slow];
fast = nums[nums[fast]];
if(slow == fast){
fast = 0;
while(nums[slow] != nums[fast]){
fast = nums[fast];
slow = nums[slow];
}
return nums[slow];
}
}
}
};
复杂度分析:
时间复杂度:O(n)。「Floyd 判圈算法」时间复杂度为线性的时间复杂度。
空间复杂度:O(1)。我们只需要常数空间存放若干变量。
解法2:二分查找
思路:
_第11张图片](http://img.e-com-net.com/image/info8/c799a29e472a46ef9ec1028e6dbdfb7a.jpg)
找到不正常(nums中值为该下标的数重复)的那个数组下标
代码:
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
while(left < right){
// 猜测中间点数重复,查找小于等于该中间数的个数,如果等于该中间数说明没有重复,区间上移动,否则该区间有重复数
int mid = left + (right - left)/2;
int count = 0;
for(auto& num:nums){
if(num<=mid) count++;
}
// 如果小于等于该数的值的数量等于该数,则向上滑动区间
if(count<=mid){
left = mid + 1;
}else{
right = mid;
}
}
return left;
}
};
复杂度分析:
时间复杂度:O(nlogn),其中 n 为 nums 数组的长度。二分查找最多需要二分 O(logn) 次,每次判断的时候需要O(n) 遍历nums 数组求解小于等于 mid 的数的个数,因此总时间复杂度为 O(nlogn)。
空间复杂度:O(1)。我们只需要常数空间存放若干变量。
15. 三数之和
力扣链接
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = []
输出:[]
示例 3:
输入:nums = [0]
输出:[]
提示:
0 <= nums.length <= 3000
-105 <= nums[i] <= 105
解法1:双指针
思路:
(1)这道题目使用哈希法并不十分合适,因为在去重的操作中有很多细节需要注意,在面试中很难直接写出没有bug的代码。
而且使用哈希法 在使用两层for循环的时候,能做的剪枝操作很有限,虽然时间复杂度是 O ( n 2 ) O(n^2) O(n2),也是可以在leetcode上通过,但是程序的执行时间依然比较长 。
(2)接下来我来介绍另一个解法:双指针法,这道题目使用双指针法 要比哈希法高效一些,那么来讲解一下具体实现的思路。
拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i] b = nums[left] c = nums[right]。
接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
代码:
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
sort(nums.begin(),nums.end());
for(int i = 0;i<nums.size();i++){
if(nums[i] > 0) return result;
//去重
if(i>0 && nums[i] == nums[i-1] ) continue;
int left = i+1;
int right = nums.size() - 1;
while(right > left){
if(nums[i] + nums[left] + nums[right] < 0) left++;
else if(nums[i] + nums[left] + nums[right] > 0) right--;
else{
result.push_back(vector<int>{nums[i],nums[left],nums[right]});
去重逻辑应该放在找到一个三元组之后
while(right>left && nums[right] == nums[right-1]) right--;
while(right>left && nums[left] == nums[left+1]) left++;
right--;
left++;
}
}
}
return result;
}
};
复杂度分析:
时间复杂度: O ( n 2 ) O(n^2) O(n2)。
_第13张图片](http://img.e-com-net.com/image/info8/214630a1bd984950a477a764779f7aa8.jpg)
相似题目:611. 有效三角形的个数
力扣链接
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。
示例 1:
输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3
示例 2:
输入: nums = [4,2,3,4]
输出: 4
提示:
1 <= nums.length <= 1000
0 <= nums[i] <= 1000
解法1:双指针
class Solution {
public:
int triangleNumber(vector<int>& nums) {
int res = 0;
int n = nums.size();
sort(nums.begin(),nums.end());
for(int i = n-1;i>=2;i--){
int left = 0, right = i-1;
while(left < right){
if(nums[left] + nums[right] > nums[i]){
res+= right - left;//i, r 和从l到r-1都可组成三角形,个数为 (r-1) - l + 1 = r - l
right--;
}else{
left++;
}
}
}
return res;
}
};
相似题目:16. 最接近的三数之和
力扣链接
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
示例 1:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
示例 2:
输入:nums = [0,0,0], target = 1
输出:0
提示:
3 <= nums.length <= 1000
-1000 <= nums[i] <= 1000
-104 <= target <= 104
解法1:双指针+排序
class Solution {
public:
int threeSumClosest(vector<int>& nums, int target) {
sort(nums.begin(),nums.end());
int n = nums.size();
int clostSum = nums[0] + nums[1] + nums[2];
for(int i = 0;i<n-2;i++){
if(i > 0 && nums[i-1] == nums[i]) continue;
int left = i+1, right = n - 1;
while(left<right){
int threeSum = nums[i] + nums[left] + nums[right];
if(abs(threeSum-target)<abs(clostSum-target)){
clostSum = threeSum;
}
if(threeSum > target){
right--;
while(left < right && nums[right] == nums[right+1]){
right--;
}
}
else if(threeSum < target){
left++;
while(left < right && nums[left] == nums[left-1]){
left++;
}
}else return target;
}
}
return clostSum;
}
};
相似题目:1. 两数之和
力扣链接
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
进阶:你可以想出一个时间复杂度小于 O(n2) 的算法吗?
解法1:哈希表
代码:
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> umap;
for(int i = 0;i<nums.size();i++){
auto iter = umap.find(target-nums[i]);
if(iter != umap.end()) return {iter->second,i};
umap.insert(pair<int,int>(nums[i],i));
}
return {};
}
};
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> umap;//target-i i
for(int i = 0;i<nums.size();i++){
umap[target-nums[i]] = i;
}
vector<int> result;
for(int i = 0;i<nums.size();i++){
if(umap.count(nums[i]) > 0 && umap[nums[i]] != i) {
result.push_back(i);
result.push_back(umap[nums[i]]);
break;
}
}
return result;
}
};
31. 下一个排列
likou
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 100
解法1:两遍扫描+双指针
代码:
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int i = nums.size() - 2;
while(i >= 0 && nums[i+1] <= nums[i]) i--;
int firstIndex = i;
if(firstIndex >= 0){
int j = nums.size() - 1;
while(nums[j] <= nums[firstIndex]) j--;
int secondIndex = j;
swap(nums[firstIndex],nums[secondIndex]);
}
reverse(nums.begin()+firstIndex+1,nums.end());
}
};
165. 比较版本号
力扣链接
给你两个版本号 version1 和 version2 ,请你比较它们。
版本号由一个或多个修订号组成,各修订号由一个 ‘.’ 连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,2.5.33 和 0.1 都是有效的版本号。
比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 忽略任何前导零后的整数值 。也就是说,修订号 1 和修订号 001 相等 。如果版本号没有指定某个下标处的修订号,则该修订号视为 0 。例如,版本 1.0 小于版本 1.1 ,因为它们下标为 0 的修订号相同,而下标为 1 的修订号分别为 0 和 1 ,0 < 1 。
返回规则如下:
如果 version1 > version2 返回 1,
如果 version1 < version2 返回 -1,
除此之外返回 0。
示例 1:
输入:version1 = “1.01”, version2 = “1.001”
输出:0
解释:忽略前导零,“01” 和 “001” 都表示相同的整数 “1”
示例 2:
输入:version1 = “1.0”, version2 = “1.0.0”
输出:0
解释:version1 没有指定下标为 2 的修订号,即视为 “0”
示例 3:
输入:version1 = “0.1”, version2 = “1.1”
输出:-1
解释:version1 中下标为 0 的修订号是 “0”,version2 中下标为 0 的修订号是 “1” 。0 < 1,所以 version1 < version2
提示:
1 <= version1.length, version2.length <= 500
version1 和 version2 仅包含数字和 ‘.’
version1 和 version2 都是 有效版本号
version1 和 version2 的所有修订号都可以存储在 32 位整数 中
解法1:双指针
class Solution {
public:
int compareVersion(string version1, string version2) {
int i = 0, j = 0;
int m = version1.size(), n = version2.size();
while(i < m || j < n){
long a = 0, b = 0;
while(i < m && version1[i] != '.') a = a*10 + version1[i++] - '0';
while(j < n && version2[j] != '.') b = b*10 + version2[j++] - '0';
if(a > b) return 1;
else if(a < b) return -1;
i++;
j++;
}
return 0;
}
};
75. 颜色分类
力扣链接
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
提示:
n == nums.length
1 <= n <= 300
nums[i] 为 0、1 或 2
进阶:
你可以不使用代码库中的排序函数来解决这道题吗?
你能想出一个仅使用常数空间的一趟扫描算法吗?
解法1:双指针+一次遍历
思路:
0,1,2 排序。一次遍历,如果是0,则移动到表头,如果是2,则移动到表尾,不用考虑1。0和2处理完,1还会有错吗?
代码:
class Solution {
public:
void sortColors(vector<int>& nums) {
//双指针 一次遍历
int p0 = 0, p2 = nums.size() - 1;
for(int i = 0;i<=p2;i++){
while(i <= p2 && nums[i] == 2){
swap(nums[i],nums[p2]);
p2--;
}
if(nums[i] == 0){
swap(nums[i],nums[p0]);
p0++;
}
}
}
};
解法2:双指针+一次遍历
class Solution {
public:
void sortColors(vector<int>& nums) {
//双指针 一次遍历
int p0 = 0, p1 = 0;
for(int i = 0;i<nums.size();i++){
if(nums[i] == 1){
swap(nums[i],nums[p1]);
p1++;
}
if(nums[i] == 0){
swap(nums[i],nums[p0]);
if(p0 < p1){//这个时候的nums[i]有可能是1
swap(nums[i],nums[p1]);
}
p0++;
p1++;
}
}
}
};
缩减搜索空间的思想
11. 盛最多水的容器
力扣链接
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
示例 1:
_第23张图片](http://img.e-com-net.com/image/info8/1ac031e7557148fd8aacc0fc824c5407.jpg)
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
示例 3:
输入:height = [4,3,2,1,4]
输出:16
示例 4:
输入:height = [1,2,1]
输出:2
提示:
n == height.length
2 <= n <= 105
0 <= height[i] <= 104
解法1:双指针
class Solution {
public:
int maxArea(vector<int>& height) {
//双指针
int left = 0, right = height.size()-1;
int result = (right-left)*min(height[left],height[right]);
while(left < right){
if (height[left] < height[right]) left++;
else right--;
result = max((right-left)*min(height[left],height[right]),result);
}
return result;
}
};
复杂度分析:
时间复杂度 O(N) : 双指针遍历一次底边宽度 N 。
空间复杂度 O(1) : 变量 i , j , res 使用常数额外空间。
240. 搜索二维矩阵 II
力扣链接
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:
_第28张图片](http://img.e-com-net.com/image/info8/ac50f9c9ed2944fdae6d2f21d351ab2f.jpg)
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
提示:
m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109
解法1:双指针+二叉搜索树
思路:
该做法则与 (题解)74. 搜索二维矩阵 的「解法二」完全一致。
我们可以将二维矩阵抽象成「以右上角为根的 BST」:
_第29张图片](http://img.e-com-net.com/image/info8/d4f023b4d5134954bf1d65413153f570.jpg)
那么我们可以从根(右上角)开始搜索,如果当前的节点不等于目标值,可以按照树的搜索顺序进行:
当前节点「大于」目标值,搜索当前节点的「左子树」,也就是当前矩阵位置的「左方格子」,即 c–
当前节点「小于」目标值,搜索当前节点的「右子树」,也就是当前矩阵位置的「下方格子」,即 r++
代码:
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
int row = 0, col = n -1;
while(row<m && col >=0){
if(matrix[row][col] < target) row++;
else if(matrix[row][col] > target) col--;
else return true;
}
return false;
}
};
复杂度分析:
时间复杂度:O(m + n)
空间复杂度:O(1)
167. 两数之和 II - 输入有序数组
力扣链接
给定一个已按照 非递减顺序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ,所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
提示:
2 <= numbers.length <= 3 * 104
-1000 <= numbers[i] <= 1000
numbers 按 非递减顺序 排列
-1000 <= target <= 100
解法1:双指针
代码:
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
vector<int> result;
int right = numbers.size() -1;
for(int i = 0;i<numbers.size();i++){
if(numbers[i] > target) return result;
while(numbers[right] + numbers[i] > target) right--;
if (numbers[right] + numbers[i] == target){
result.push_back(i+1);
result.push_back(right+1);
return result;
}
}
return result;
}
};
|||||||||||||||| 滑动窗口 ||||||||||||||||||
992. K 个不同整数的子数组
力扣链接
给定一个正整数数组 A,如果 A 的某个子数组中不同整数的个数恰好为 K,则称 A 的这个连续、不一定不同的子数组为好子数组。
(例如,[1,2,3,1,2] 中有 3 个不同的整数:1,2,以及 3。)
返回 A 中好子数组的数目。
示例 1:
输入:A = [1,2,1,2,3], K = 2
输出:7
解释:恰好由 2 个不同整数组成的子数组:[1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].
示例 2:
输入:A = [1,2,1,3,4], K = 3
输出:3
解释:恰好由 3 个不同整数组成的子数组:[1,2,1,3], [2,1,3], [1,3,4].
提示:
1 <= A.length <= 20000
1 <= A[i] <= A.length
1 <= K <= A.length
解法1:双指针(滑动窗口)
思路:
(1)
_第33张图片](http://img.e-com-net.com/image/info8/fd4cb32309404071ab9a09d336b2b766.jpg)
_第34张图片](http://img.e-com-net.com/image/info8/98f4b9f14ad645a3bb156ee7c0945590.jpg)
(2)实现函数 atMostWithKDistinct(A, K) ,表示**「最多存在 KK 个不同整数的子区间的个数」**。于是 atMostWithKDistinct(A, K) - atMostWithKDistinct(A, K - 1) 即为所求。
代码:
class Solution {
public:
int mostDistanct(vector<int>& nums, int k){
unordered_map<int,int> umap;
int left = 0, right = 0, result = 0;
while(right < nums.size()){// [left, right)
umap[nums[right]]++;
right++;
while(umap.size() > k){
umap[nums[left]]--;
if(umap[nums[left]] == 0) umap.erase(nums[left]);
left++;
}
result += right - left;
}
return result;
}
int subarraysWithKDistinct(vector<int>& nums, int k) {
return mostDistanct(nums, k) - mostDistanct(nums, k - 1);
}
};
为什么可以用新子数组的长度即 【right - left】来表示增加的子数组个数呢?
可以借鉴动态规划的思想,举个例子就好理解了:
当满足条件的子数组从 [A,B,C] 增加到 [A,B,C,D] 时,新子数组的长度为 4,同时增加的子数组为 [D], [C,D], [B,C,D], [A,B,C,D] 也为4。
复杂度分析:
时间复杂度:O(n),其中 n是数组长度。我们至多只需要遍历该数组2次(右指针和左指针各一次)。
空间复杂度:O(n),其中 n是数组长度。我们需要记录每一个数的出现次数,本题中数的大小不超过数组长度。
相似题目:904. 水果成篮
力扣链接
你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。
你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
你只有 两个 篮子,并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘,你必须从 每棵 树(包括开始采摘的树)上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次,你将会向右移动到下一棵树,并继续采摘。
一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。
给你一个整数数组 fruits ,返回你可以收集的水果的 最大 数目。
示例 1:
输入:fruits = [1,2,1]
输出:3
解释:可以采摘全部 3 棵树。
示例 2:
输入:fruits = [0,1,2,2]
输出:3
解释:可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘,则只能采摘 [0,1] 这两棵树。
示例 3:
输入:fruits = [1,2,3,2,2]
输出:4
解释:可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘,则只能采摘 [1,2] 这两棵树。
示例 4:
输入:fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出:5
解释:可以采摘 [1,2,1,1,2] 这五棵树。
提示:
1 <= fruits.length <= 105
0 <= fruits[i] < fruits.length
解法1:双指针(滑动窗口)
思路:
代码:
class Solution {
public:
int totalFruit(vector<int>& fruits) {
unordered_map<int,int> umap;
int left = 0, right = 0, result = 0;
while(right < fruits.size()){
umap[fruits[right]]++;
right++;
while(umap.size() > 2){
umap[fruits[left]]--;
if(umap[fruits[left]] == 0) umap.erase(fruits[left]);
left++;
}
result = max(result,right-left);
}
return result;
}
};
复杂度分析:
时间复杂度:O(N),其中 N 是 tree 的长度。
空间复杂度:O(N)。
相似题目:76. 最小覆盖子串
力扣链接
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
示例 2:
输入:s = “a”, t = “a”
输出:“a”
示例 3:
输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中,
因此没有符合条件的子字符串,返回空字符串。
提示:
1 <= s.length, t.length <= 105
s 和 t 由英文字母组成
进阶:你能设计一个在 o(n) 时间内解决此问题的算法吗?
解法1:滑动窗口
思路:
(滑动窗口) O(n)
这道题要求我们返回字符串 s中包含字符串 t 的全部字符的最小窗口,我们利用滑动窗口的思想解决这个问题。因此我们需要两个哈希表,hs哈希表维护的是s字符串中滑动窗口中各个字符出现多少次,ht哈希表维护的是t字符串各个字符出现多少次。如果hs哈希表中包含ht哈希表中的所有字符,并且对应的个数都不小于ht哈希表中各个字符的个数,那么说明当前的窗口是可行的,可行中的长度最短的滑动窗口就是答案。
_第35张图片](http://img.e-com-net.com/image/info8/f826867b2a2a45c3a569e7934e56abfc.jpg)
过程如下:
1、遍历t字符串,用ht哈希表记录t字符串各个字符出现的次数。
_第36张图片](http://img.e-com-net.com/image/info8/fd23e9da92044a44b11042448444e81f.jpg)
2、定义两个指针j和i,j指针用于收缩窗口,i指针用于延伸窗口,则区间[j,i]表示当前滑动窗口。首先让i和j指针都指向字符串s开头,然后枚举整个字符串s ,枚举过程中,不断增加i使滑动窗口增大,相当于向右扩展滑动窗口。
_第37张图片](http://img.e-com-net.com/image/info8/1c42047b917a4f9698d2643155211570.jpg)
3、每次向右扩展滑动窗口一步,将s[i]加入滑动窗口中,而新加入了s[i],相当于滑动窗口维护的字符数加一,即hs[s[i]]++。
_第38张图片](http://img.e-com-net.com/image/info8/27e3e8537feb4a03a7782de7eda1bce5.jpg)
4、对于新加入的字符s[i],如果hs[s[i]] <= ht[s[i]],说明当前新加入的字符s[i]是必需的,且还未到达字符串t所要求的数量。我们还需要事先定义一个cnt变量, cnt维护的是s字符串[j,i]区间中满足t字符串的元素的个数,记录相对应字符的总数。新加入的字符s[i]必需,则cnt++。
5、我们向右扩展滑动窗口的同时也不能忘记收缩滑动窗口。因此当hs[s[j]] > ht[s[j]时,说明hs哈希表中s[j]的数量多于ht哈希表中s[j]的数量,此时我们就需要向右收缩滑动窗口,j++并使hs[s[j]]–,即hs[s[j ++ ]] --。
6、当cnt == t.size时,说明此时滑动窗口包含符串 t 的全部字符。我们重复上述过程找到最小窗口即为答案。
_第39张图片](http://img.e-com-net.com/image/info8/c656be52503f4e929e49bf36ae5169ac.jpg)
时间复杂度分析: 两个指针都严格递增,最多移动 n 次,所以总时间复杂度是 O(n)。
代码:
class Solution {
public:
string minWindow(string s, string t) {
unordered_map<char,int> sMap,tMap;
for(auto& c:t) tMap[c]++;
string result;
int cnt = 0;
int left = 0, right = 0;
while(right < s.size()){//[left,right)
sMap[s[right]]++;
if(sMap[s[right]] <= tMap[s[right]]) cnt++;//必须加入的元素
right++;
while(sMap[s[left]] > tMap[s[left]]){
sMap[s[left]]--;
left++;
}
if(cnt == t.size()){
if(result.empty() || right-left<result.size()){
//result为空或遇到了更短的长度
result = s.substr(left,right-left);
}
}
}
return result;
}
};
3. 无重复字符的最长子串
力扣链接
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
示例 3:
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
示例 4:
输入: s = “”
输出: 0
提示:
0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成
解法1:滑动窗口+哈希
思路:
这道题主要用到思路是:滑动窗口
什么是滑动窗口?
其实就是一个队列,比如例题中的 abcabcbb,进入这个队列(窗口)为 abc 满足题目要求,当再进入 a,队列变成了 abca,这时候不满足要求。所以,我们要移动这个队列!
如何移动?
我们只要把队列的左边的元素移出就行了,直到满足题目要求!
一直维持这样的队列,找出队列出现最长的长度时候,求出解!
时间复杂度:O(n)
代码1:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<char,int> umap;
int left = 0, right = 0, result = 0;
while(right < s.size()){
if(umap[s[right]] == 0){//不是重复字符,右指针右移
umap[s[right]]++;
right++;
}else{//是重复字符,左指针右移
umap[s[left]]--;
left++;
}
result = max(result,right-left);
}
return result;
}
};
代码2:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
if (s.size() == 0) return 0;
unordered_set<char> uset;
int left = 0;
int count = 0;
for(int right = 0;right<s.size();right++){
while(uset.find(s[right])!=uset.end()) {
uset.erase(s[left]);
left++;
}
count = max(count,right-left+1);
uset.insert(s[right]);
}
return count;
}
};
424. 替换后的最长重复字符
力扣链接
给你一个仅由大写英文字母组成的字符串,你可以将任意位置上的字符替换成另外的字符,总共可最多替换 k 次。在执行上述操作后,找到包含重复字母的最长子串的长度。
注意:字符串长度 和 k 不会超过 104。
示例 1:
输入:s = “ABAB”, k = 2
输出:4
解释:用两个’A’替换为两个’B’,反之亦然。
示例 2:
输入:s = “AABABBA”, k = 1
输出:4
解释:
将中间的一个’A’替换为’B’,字符串变为 “AABBBBA”。
子串 “BBBB” 有最长重复字母, 答案为 4。
解法1:滑动窗口
思路:
我们可以枚举字符串中的每一个位置作为右端点,然后找到其最远的左端点的位置,满足该区间内除了出现次数最多的那一类字符之外,剩余的字符(即非最长重复字符)数量不超过 k个。
代码:
class Solution {
public:
int characterReplacement(string s, int k) {
unordered_map<char,int> umap;
int left = 0, right = 0, result = 0, maxCnt = 0;
while(right < s.size()){
umap[s[right]]++;
maxCnt = max(maxCnt,umap[s[right]]);
right++;
while(right - left > maxCnt + k){
umap[s[left]]--;
left++;
}
result = max(result,right - left);
}
return result;
}
};
相似题目:485. 最大连续 1 的个数
力扣链接
给定一个二进制数组, 计算其中最大连续 1 的个数。
示例:
输入:[1,1,0,1,1,1]
输出:3
解释:开头的两位和最后的三位都是连续 1 ,所以最大连续 1 的个数是 3.
提示:
输入的数组只包含 0 和 1 。
输入数组的长度是正整数,且不超过 10,000。
解法1:数组+一次遍历
思路:
为了得到数组中最大连续 1 的个数,需要遍历数组,并记录最大的连续 11的个数和当前的连续 1 的个数。如果当前元素是 1,则将当前的连续 1 的个数加 1,否则,使用之前的连续 1 的个数更新最大的连续 1 的个数,并将当前的连续 1 的个数清零。
遍历数组结束之后,需要再次使用当前的连续 1的个数更新最大的连续 1 的个数,因为数组的最后一个元素可能是 1,且最长连续 1 的子数组可能出现在数组的末尾,如果遍历数组结束之后不更新最大的连续 1 的个数,则会导致结果错误。
代码:
class Solution {
public:
int findMaxConsecutiveOnes(vector<int>& nums) {
int count = 0, result = 0;
for(int i = 0;i<nums.size();i++){
if(nums[i] == 1) count++;
else{
result = max(result,count);
count = 0;
}
}
result = max(result,count);
return result;
}
};
剑指 Offer 59 - I. 滑动窗口的最大值
力扣链接
给定一个数组 nums 和滑动窗口的大小 k,请找出所有滑动窗口里的最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
提示:
你可以假设 k 总是有效的,在输入数组不为空的情况下,1 ≤ k ≤ 输入数组的大小。
注意:本题与主站 239 题相同:https://leetcode-cn.com/problems/sliding-window-maximum/
解法1:滑动窗口+单调队列+双向队列
思路:
这是使用单调队列的经典题目。
(1)我们需要一个队列,这个队列呢,放进去窗口里的元素,然后随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值是什么。
这个队列应该长这个样子:
class MyQueue {
public:
void pop(int value) {
}
void push(int value) {
}
int front() {
return que.front();
}
};
每次窗口移动的时候,调用que.pop(滑动窗口中移除元素的数值),que.push(滑动窗口添加元素的数值),然后que.front()就返回我们要的最大值。
这么个队列香不香,要是有现成的这种数据结构是不是更香了!可惜了,没有! 我们需要自己实现这么个队列。
然后在分析一下,队列里的元素一定是要排序的,而且要**最大值放在出队口,**要不然怎么知道最大值呢。
但如果把窗口里的元素都放进队列里,窗口移动的时候,队列需要弹出元素。那么问题来了,已经排序之后的队列 怎么能把窗口要移除的元素(这个元素可不一定是最大值)弹出呢。
其实队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队里里的元素数值是由大到小的。
那么这个维护元素单调递减的队列就叫做单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来一个单调队列
不要以为实现的单调队列就是 对窗口里面的数进行排序,如果排序的话,那和优先级队列又有什么区别了呢。
(2)对于窗口里的元素{2, 3, 5, 1 ,4},单调队列里只维护{5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口经行滑动呢?
设计单调队列的时候,pop,和push操作要保持如下规则:
1.pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
2.push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
那么我们用什么数据结构来实现这个单调队列呢?使用deque最为合适,常用的queue在没有指定容器的情况下,deque就是默认底层容器。
class MyQueue { //单调队列(从大到小)
public:
deque<int> que; // 使用deque来实现单调队列
// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
// 同时pop之前判断队列当前是否为空。
void pop(int value) {
if (!que.empty() && value == que.front()) {
que.pop_front();
}
}
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
// 这样就保持了队列里的数值是单调从大到小的了。
void push(int value) {
while (!que.empty() && value > que.back()) {
que.pop_back();
}
que.push_back(value);
}
// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
int front() {
return que.front();
}
};
代码:
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
//单调队列
deque<int> dq;
for(int i = 0;i<k;i++){
while(!dq.empty() && nums[i] >= nums[dq.back()]){
dq.pop_back();
}
dq.push_back(i);
}
vector<int> res = {nums[dq.front()]};
for(int i = k;i<nums.size();i++){
while(!dq.empty() && nums[i] >= nums[dq.back()]){
dq.pop_back();
}
dq.push_back(i);
while(dq.front() <= i-k) dq.pop_front();
res.push_back(nums[dq.front()]);
}
return res;
}
};
复杂度分析:
时间复杂度,使用单调队列的时间复杂度是 O ( n ) O(n) O(n)。
有的同学可能想了,在队列中 push元素的过程中,还有pop操作呢,感觉不是纯粹的 O ( n ) O(n) O(n)。
其实,大家可以自己观察一下单调队列的实现,nums 中的每个元素最多也就被 push_back 和 pop_back 各一次,没有任何多余操作,所以整体的复杂度还是 O ( n ) O(n) O(n)。
空间复杂度因为我们定义一个辅助队列,所以是 O ( k ) O(k) O(k)
解法2:优先队列+滑动窗口
代码:
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
if(nums.size() == 0) return {};
//大根堆
priority_queue<pair<int,int>> pq;//num[i]--位置
for(int i = 0;i<k;i++){
pq.push({nums[i],i});
}
vector<int> result;
result.push_back(pq.top().first);
for(int i = k;i<nums.size();i++){
pq.push({nums[i],i});
while(pq.top().second <= i-k){
pq.pop();
}
result.push_back(pq.top().first);
}
return result;
}
};
相似题目:剑指 Offer 59 - II. 队列的最大值
力扣链接
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1
示例 1:
输入:
[“MaxQueue”,“push_back”,“push_back”,“max_value”,“pop_front”,“max_value”]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]
示例 2:
输入:
[“MaxQueue”,“pop_front”,“max_value”]
[[],[],[]]
输出: [null,-1,-1]
限制:
1 <= push_back,pop_front,max_value的总操作数 <= 10000
1 <= value <= 10^5
解法1:单调队列+滑动窗口
class MaxQueue {
public:
queue<int> q;
deque<int> dq;
MaxQueue() {
}
int max_value() {
if(dq.empty()) return -1;
return dq.front();
}
void push_back(int value) {
while(!dq.empty() && value > dq.back()){
dq.pop_back();
}
dq.push_back(value);
q.push(value);
}
int pop_front() {
if(q.empty()) return -1;
int result = q.front();
if(result == dq.front()){
dq.pop_front();
}
q.pop();
return result;
}
};
/**
* Your MaxQueue object will be instantiated and called as such:
* MaxQueue* obj = new MaxQueue();
* int param_1 = obj->max_value();
* obj->push_back(value);
* int param_3 = obj->pop_front();
*/
1052. 爱生气的书店老板
力扣链接
有一个书店老板,他的书店开了 n 分钟。每分钟都有一些顾客进入这家商店。给定一个长度为 n 的整数数组 customers ,其中 customers[i] 是在第 i 分钟开始时进入商店的顾客的编号,所有这些顾客在第 i 分钟结束后离开。
在某些时候,书店老板会生气。 如果书店老板在第 i 分钟生气,那么 grumpy[i] = 1,否则 grumpy[i] = 0。
当书店老板生气时,那一分钟的顾客就会不满意,若老板不生气则顾客是满意的。
书店老板知道一个秘密技巧,能抑制自己的情绪,可以让自己连续 minutes 分钟不生气,但却只能使用一次。
请你返回 这一天营业下来,最多有多少客户能够感到满意 。
示例 1:
输入:customers = [1,0,1,2,1,1,7,5], grumpy = [0,1,0,1,0,1,0,1], minutes = 3
输出:16
解释:书店老板在最后 3 分钟保持冷静。
感到满意的最大客户数量 = 1 + 1 + 1 + 1 + 7 + 5 = 16.
示例 2:
输入:customers = [1], grumpy = [0], minutes = 1
输出:1
提示:
n == customers.length == grumpy.length
1 <= minutes <= n <= 2 * 104
0 <= customers[i] <= 1000
grumpy[i] == 0 or 1
解法1:数组+滑动窗口
代码:
class Solution {
public:
int maxSatisfied(vector<int>& customers, vector<int>& grumpy, int minutes) {
int n = customers.size();
int sum = 0, maxN = 0;//不生气时的总数 生气区间内使用技巧的最大值
for(int i = 0;i<n;i++){
if(grumpy[i] == 0){
sum += customers[i];
customers[i] = 0;
}
}
int num = 0;
for(int i = 0, j = 0;i<n;i++){
num += customers[i];
if(i-j+1>minutes){
num -= customers[j];
j++;
}
maxN = max(maxN,num);
}
return sum + maxN;
}
};
209. 长度最小的子数组
力扣链接
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
进阶:
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。
解法1:滑动窗口
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
//滑动窗口
int result = INT_MAX;
int sum = 0;
for(int i = 0, j = 0;j<nums.size();j++){
sum += nums[j];
while(sum >= target){
result = min(j-i+1,result);
sum -= nums[i];
i++;
}
}
return result == INT_MAX ? 0:result;
}
};
相似题目:718. 最长重复子数组
力扣链接
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
示例 2:
输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出:5
提示:
1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 100
解法1:动态规划
确定dp数组(dp table)以及下标的含义
dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。 (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
int n1 = nums1.size(), n2 = nums2.size();
vector<vector<int>> dp(n1+1,vector<int>(n2+1,0));
int res = 0;
for(int i = 1;i<=n1;i++){
for(int j = 1;j<=n2;j++){
if(nums1[i-1]== nums2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
}
res = max(res, dp[i][j]);
}
}
return res;
}
};
567. 字符串的排列
力扣链接
给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true ;否则,返回 false 。
换句话说,s1 的排列之一是 s2 的 子串 。
示例 1:
输入:s1 = “ab” s2 = “eidbaooo”
输出:true
解释:s2 包含 s1 的排列之一 (“ba”).
示例 2:
输入:s1= “ab” s2 = “eidboaoo”
输出:false
提示:
1 <= s1.length, s2.length <= 104
s1 和 s2 仅包含小写字母
解法1:滑动窗口
class Solution {
public:
bool checkInclusion(string s1, string s2) {
//滑动窗口
unordered_map<char,int> s1Map, s2Map;
for(char c:s1) s1Map[c]++;
int slow = 0, fast = 0;
for(;fast<s2.size();fast++){
s2Map[s2[fast]]++;
while(s2Map[s2[fast]] > s1Map[s2[fast]]){
s2Map[s2[slow]]--;
slow++;
}
if(fast - slow + 1 == s1.size()) return true;
}
return false;
}
};
_第1张图片](http://img.e-com-net.com/image/info8/cc916214d1b54cdd831e2636a50f1709.jpg)
_第2张图片](http://img.e-com-net.com/image/info8/2346f7aac0a84d0096f8d5bd6ded1dad.jpg)
_第4张图片](http://img.e-com-net.com/image/info8/970c71acaccd4fba80c1d37e64f9099b.jpg)
_第5张图片](http://img.e-com-net.com/image/info8/f7da410b5d0c4d0d9041142998f771c6.jpg)
_第6张图片](http://img.e-com-net.com/image/info8/110bbd5549454fd382a73b57b035003c.jpg)
_第7张图片](http://img.e-com-net.com/image/info8/400f8cb72502416e800b98a78da3c5cc.jpg)
_第8张图片](http://img.e-com-net.com/image/info8/ba0ed3c7200948868d6b6c85ed175fff.jpg)
_第9张图片](http://img.e-com-net.com/image/info8/ba605cdf3fc0459f9f95653fe0dbd1c0.jpg)
_第10张图片](http://img.e-com-net.com/image/info8/7a7ac314549c4f79b3130f8b3d86f0a2.jpg)
_第12张图片](http://img.e-com-net.com/image/info8/937875025ab541be9d85e654e2c740c1.jpg)
_第14张图片](http://img.e-com-net.com/image/info8/8a2c95ff5f7d43d6a2eb7484dbbdab10.jpg)
_第15张图片](http://img.e-com-net.com/image/info8/5d41cb58466e42298204b9ec7983ab52.jpg)
_第16张图片](http://img.e-com-net.com/image/info8/c834ec55b1d74b4faa20cc05e537587b.jpg)
_第17张图片](http://img.e-com-net.com/image/info8/db9d144bf2dc4912a2c61cf49678538c.jpg)
_第18张图片](http://img.e-com-net.com/image/info8/f64d842f6aa04f3ab06c5eda5aaa48cc.jpg)
_第19张图片](http://img.e-com-net.com/image/info8/9592a4c0642d4849adc4c95f702cf4fe.jpg)
_第20张图片](http://img.e-com-net.com/image/info8/7b0ceec8f41d4547a5c3ef7f39c40ac7.jpg)
_第21张图片](http://img.e-com-net.com/image/info8/86eb4e5978c544eab0663ba17fe55a44.jpg)
_第22张图片](http://img.e-com-net.com/image/info8/3ea459ae3f344229ae14f220a68f2644.jpg)
_第24张图片](http://img.e-com-net.com/image/info8/58f02b70a33545bc9d52b8e1986ddae5.jpg)
_第25张图片](http://img.e-com-net.com/image/info8/a95d308b556a49be8894b2f9bb5207b3.jpg)
_第26张图片](http://img.e-com-net.com/image/info8/cff138dfd7624f118af371c42ba19755.jpg)
_第27张图片](http://img.e-com-net.com/image/info8/b9cc258af86347568024279b2be1c464.jpg)
_第30张图片](http://img.e-com-net.com/image/info8/2d1e405edb6a46138e9a9453960ec420.jpg)
_第31张图片](http://img.e-com-net.com/image/info8/c33ca34ac15c4db7894b824c5df10c25.jpg)
_第32张图片](http://img.e-com-net.com/image/info8/704292a1f5de441cb6c231f01551c54e.jpg)
_第40张图片](http://img.e-com-net.com/image/info8/9df04ac3b5fb4b6cbf6e21b9de0cf0a6.jpg)
_第41张图片](http://img.e-com-net.com/image/info8/e817fa17776747e08c6c97ff0af400c1.jpg)
_第42张图片](http://img.e-com-net.com/image/info8/c0c6ed7dab18434381a90d975c771a01.jpg)
_第43张图片](http://img.e-com-net.com/image/info8/7fed2d00c44b4e81b0145f82dd14ac37.jpg)
_第44张图片](http://img.e-com-net.com/image/info8/f2e6763e80ac458694be97913691fa2b.jpg)
_第45张图片](http://img.e-com-net.com/image/info8/8aa2dbf8bbd54e6a912c2794d497c19f.jpg)
_第46张图片](http://img.e-com-net.com/image/info8/49fc0bee7e004a14be4eb52d71141e25.jpg)
