数据结构与算法-线段树(segment-tree)
为什么要使用线段树
若要查询某个区间的情况时,使用普通数组查询和更新时间为O(n)
而线段树只需要O(logn)
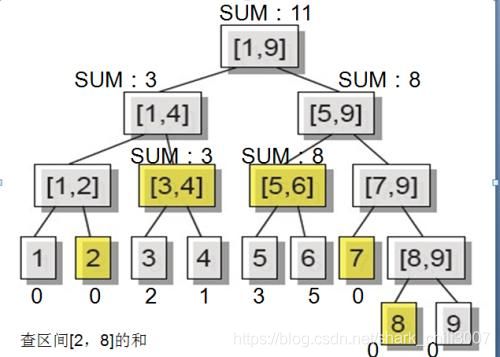
线段树图
线段树特点
- 线段树不是完全二叉树
- 线段树是平衡二叉树
线段树的研究与设计
前言
设计
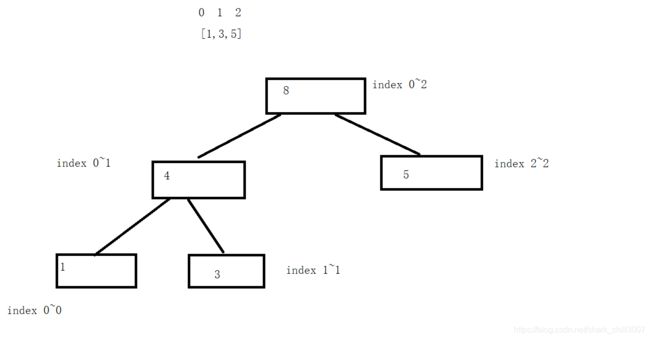
这里我们使用数组的实现,由于线段树区间是固定的,所以不涉及插入操作,我们可以按照如下如推到得出通用的线段树空间计算公式:
解:
线段树如上图所示,也是二叉树,所以每一层的节点树为2 ^(h-1)
所以每个线段树的最后一层节点数最多是2^(h-1)
由二叉树求节点数公式为:2^h -1
所以线段树从第一层到倒数第二层节点数为:
2^(h-1)-1 ≈最后一层节点数
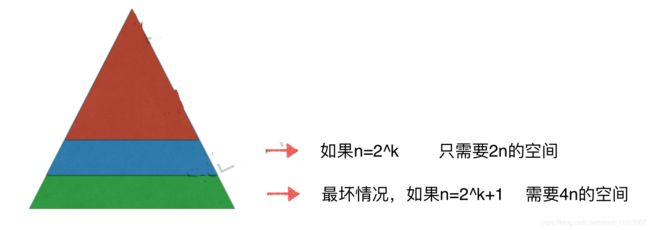
所以:
常规情况下,若有n个节点,线段树需要2n个空间,最多需要4n(即最后一层不够装,还要往下)
线段树的实现
基础实现
public class SegmentTree<E> {
private E[] data;
private E[] tree;
private Merger<E> merger;
public SegmentTree(E[] arr, Merger<E> merger) {
data = (E[]) new Object[arr.length];
this.merger = merger;
for (int i = 0; i < arr.length; i++) {
data[i] = arr[i];
}
tree = (E[]) new Object[4 * arr.length];
buildSegmentTree(0, 0, arr.length - 1);
}
public int getSize() {
return data.length;
}
public E get(int index) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("index outbound");
return data[index];
}
private int leftChildIndex(int parentIndex) {
return (parentIndex << 1) + 1;
}
private int rightChildIndex(int parentIndex) {
return (parentIndex << 1) + 2;
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("[ ");
for (int i = 0; i < tree.length; i++) {
if (tree[i] != null)
res.append(tree[i]);
else res.append("null");
if (i != tree.length - 1) ;
res.append(", ");
}
res.append("]");
return res.toString();
}
}
创建线段树
编码思路
使用递归的方式自底向上构建一个完整的线段树
实现代码
/**
* 构建一个表示区间 [l,r]区间的线段树
*
* @param treeIndex
* @param l
* @param r
*/
private void buildSegmentTree(int treeIndex, int l, int r) {
if (l == r) {
tree[treeIndex] = data[l];
return;
}
int leftChildIndex = leftChildIndex(treeIndex);
int rightChildIndex = rightChildIndex(treeIndex);
int middleIndex = l + (r - l) / 2;
buildSegmentTree(leftChildIndex, l, middleIndex);
buildSegmentTree(rightChildIndex, middleIndex + 1, r);
tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]);
}
线段树查询
实现思路
使用递归,计算过程会出现三种情况
- 精确定位到查询区间直接返回父索引的值
- 查询的左索引区间在右半边,向右半边递归
- 查询的右索引区间在左半边,向左半边递归
- 最麻烦的一种情况,区间在左右两边,分别递归查找
实现代码
/**
* 返回区间[queryL, queryR]的值
* @param queryL
* @param queryR
* @return
*/
public E query(int queryL, int queryR){
if(queryL < 0 || queryL >= data.length ||
queryR < 0 || queryR >= data.length || queryL > queryR)
throw new IllegalArgumentException("Index is illegal.");
return query(0, 0, data.length - 1, queryL, queryR);
}
/**
* 查询以treeIndex为根的线段树 [l,r] 区间中[queryL,queryR]的值
*
* @param treeIndex
* @param l
* @param r
* @param queryL
* @param queryR
* @return
*/
private E query(int treeIndex, int l, int r, int queryL, int queryR) {
if (l == queryL && r == queryR)
return tree[treeIndex];
int middleIndex = l + (r - l) / 2;
int leftChildIndex = leftChildIndex(treeIndex);
int rightChildIndex = rightChildIndex(treeIndex);
if (queryL >= middleIndex + 1) {
return query(rightChildIndex, middleIndex + 1, r, queryL, queryR);
}
if (queryR <= middleIndex)
return query(leftChildIndex,l,middleIndex,queryL,queryR );
E leftResult = query(leftChildIndex, l, middleIndex, queryL, middleIndex);
E rightResult = query(rightChildIndex, middleIndex+1, r, middleIndex+1, queryR);
return merger.merge(leftResult,rightResult);
}
线段树更新
实现思路
递归
实现代码
public void set(int index, E e){
if(index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal");
data[index] = e;
set(0, 0, data.length - 1, index, e);
}
/**
* 将索引为desIndex的节点值修改为value
* @param treeIndex
* @param l
* @param r
* @param desIndex
* @param value
*/
private void set(int treeIndex, int l, int r, int desIndex, E value) {
if (l == r) {
tree[treeIndex]=value;
return;
}
int leftChildIndex = leftChildIndex(treeIndex);
int rightChildIndex = rightChildIndex(treeIndex);
int middle=l+(r-l)/2;
if (l>=middle+1)
set(rightChildIndex,middle+1,r,desIndex,value);
if (r<=middle)
set(leftChildIndex,l,middle,desIndex,value);
tree[treeIndex]=merger.merge(tree[leftChildIndex],tree[rightChildIndex]);
}
leetcode中关于线段树的题目
303. 区域和检索 - 数组不可变
题目链接
303. 区域和检索 - 数组不可变
实现思路1
基于上述query代码加以改造
class NumArray {
private SegmentTree<Integer> segmentTree;
public NumArray(int[] nums) {
if(nums.length > 0){
Integer[] data = new Integer[nums.length];
for (int i = 0; i < nums.length; i++)
data[i] = nums[i];
segmentTree = new SegmentTree<>(data, (a, b) -> a + b);
}
}
public int sumRange(int i, int j) {
if(segmentTree == null)
throw new IllegalArgumentException("Segment Tree is null");
return segmentTree.query(i, j);
}
}
实现思路2
使用sum记录前n项和,如0记录0项和,1记录一个数字的和,2记录nums数组前两项和。计算区间只需传入指定传入指定区间即可。
package com.study.leetcode;
/**
* Created by Zsy on 2020/8/19.
*/
public class NumArray_303 {
private int[] sum;
public NumArray_303(int[] nums) {
sum = new int[nums.length + 1];
sum[0] = 0;
for (int i = 1; i < sum.length; i++) {
sum[i] = sum[i - 1] + nums[i - 1];
}
}
public int sumRange(int i, int j) {
return sum[j + 1] - sum[i];
}
}
307
题目链接
307. 区域和检索 - 数组可修改
实现代码
/**
* Created by Zsy on 2020/8/19.
*/
public class NumArray {
@Override
public String toString() {
return "NumArray_307{" +
"segmentTree=" + segmentTree +
'}';
}
public interface Merger<E> {
E merge(E a, E b);
}
private class SegmentTree<E> {
private E[] data;
private E[] tree;
private Merger<E> merger;
public SegmentTree(E[] arr, Merger<E> merger) {
data = (E[]) new Object[arr.length];
this.merger = merger;
for (int i = 0; i < arr.length; i++) {
data[i] = arr[i];
}
tree = (E[]) new Object[4 * arr.length];
buildSegmentTree(0, 0, arr.length - 1);
}
public int getSize() {
return data.length;
}
public E get(int index) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("index outbound");
return data[index];
}
private int leftChildIndex(int parentIndex) {
return (parentIndex << 1) + 1;
}
private int rightChildIndex(int parentIndex) {
return (parentIndex << 1) + 2;
}
/**
* 构建一个表示区间 [l,r]区间的线段树
*
* @param treeIndex
* @param l
* @param r
*/
private void buildSegmentTree(int treeIndex, int l, int r) {
if (l == r) {
tree[treeIndex] = data[l];
return;
}
int leftChildIndex = leftChildIndex(treeIndex);
int rightChildIndex = rightChildIndex(treeIndex);
int middleIndex = l + (r - l) / 2;
buildSegmentTree(leftChildIndex, l, middleIndex);
buildSegmentTree(rightChildIndex, middleIndex + 1, r);
tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]);
}
/**
* 返回区间[queryL, queryR]的值
*
* @param queryL
* @param queryR
* @return
*/
public E query(int queryL, int queryR) {
if (queryL < 0 || queryL >= data.length ||
queryR < 0 || queryR >= data.length || queryL > queryR)
throw new IllegalArgumentException("Index is illegal.");
return query(0, 0, data.length - 1, queryL, queryR);
}
/**
* 查询以treeIndex为根的线段树 [l,r] 区间中[queryL,queryR]的值
*
* @param treeIndex
* @param l
* @param r
* @param queryL
* @param queryR
* @return
*/
private E query(int treeIndex, int l, int r, int queryL, int queryR) {
if (l == queryL && r == queryR)
return tree[treeIndex];
int middleIndex = l + (r - l) / 2;
int leftChildIndex = leftChildIndex(treeIndex);
int rightChildIndex = rightChildIndex(treeIndex);
if (queryL >= middleIndex + 1) {
return query(rightChildIndex, middleIndex + 1, r, queryL, queryR);
}
if (queryR <= middleIndex)
return query(leftChildIndex, l, middleIndex, queryL, queryR);
E leftResult = query(leftChildIndex, l, middleIndex, queryL, middleIndex);
E rightResult = query(rightChildIndex, middleIndex + 1, r, middleIndex + 1, queryR);
return merger.merge(leftResult, rightResult);
}
public void set(int index, E e) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal");
data[index] = e;
set(0, 0, data.length - 1, index, e);
}
/**
* 将索引为desIndex的节点值修改为value
*
* @param treeIndex
* @param l
* @param r
* @param desIndex
* @param value
*/
private void set(int treeIndex, int l, int r, int desIndex, E value) {
if (l == r) {
tree[treeIndex] = value;
return;
}
int leftChildIndex = leftChildIndex(treeIndex);
int rightChildIndex = rightChildIndex(treeIndex);
int middle = l + (r - l) / 2;
if (desIndex >= middle + 1)
set(rightChildIndex, middle + 1, r, desIndex, value);
else
set(leftChildIndex, l, middle, desIndex, value);
tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]);
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("[ ");
for (int i = 0; i < tree.length; i++) {
if (tree[i] != null)
res.append(tree[i]);
else res.append("null");
if (i != tree.length - 1) ;
res.append(", ");
}
res.append("]");
return res.toString();
}
}
private SegmentTree<Integer> segmentTree;
public NumArray(int[] nums) {
if (nums.length != 0) {
Integer[] data = new Integer[nums.length];
for (int i = 0; i < nums.length; i++) {
data[i] = nums[i];
}
segmentTree = new SegmentTree<>(data, (a, b) -> a + b);
}
}
public void update(int i, int val) {
if (segmentTree == null)
throw new IllegalArgumentException("tree null");
segmentTree.set(i, val);
}
public int sumRange(int i, int j) {
return segmentTree.query(i, j);
}
}