python机器学习(四)线性代数回顾、多元线性回归、多项式回归、标准方程法求解、线性回归案例
回顾线性代数
矩阵
矩阵可以理解为二维数组的另一种表现形式。A矩阵为三行两列的矩阵,B矩阵为两行三列的矩阵,可以通过下标来获取矩阵的元素,下标默认都是从0开始的。 A i j : A_{ij}: Aij:表示第 i i i行,第 j j j列的元素。

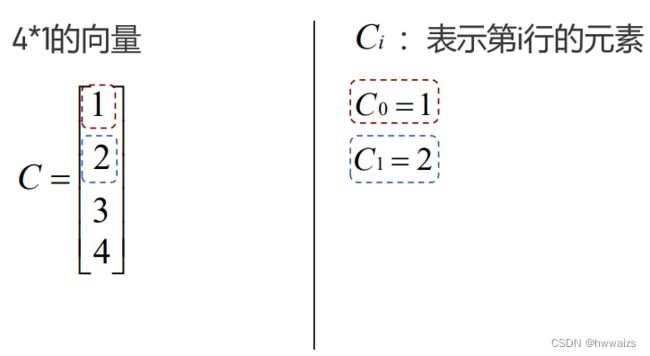
向量
矩阵与标量运算
标量与矩阵里的每一个元素进行运算,也可以想象成利用广播机制,把标量看成与矩阵同形状且每个元素都为标量的矩阵,对应位置进行运算。
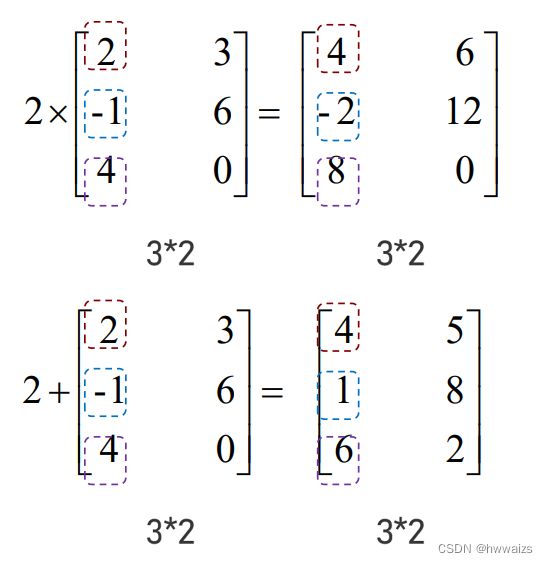
矩阵与标量之间的运算是将每个元素都与标量进行运算。
矩阵与向量运算
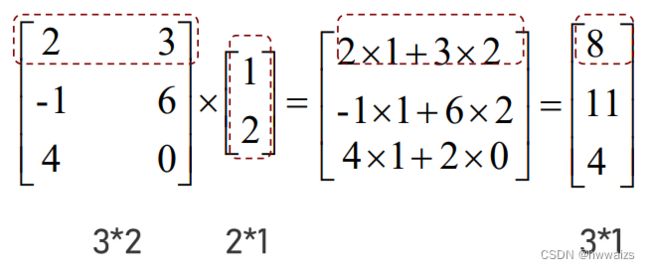
n n n行 m m m列的矩阵乘以 m m m行1列的向量,得到 n n n行1列的向量。
例题:
比如房子的大小影响房价的高低,大小作为特征数据。
某特征数据: [ 1 2 3 ] \begin{bmatrix} 1\\ 2\\3\end{bmatrix} 123 ,线性关系为: h ( x ) = 2 x + 1 h(x)=2x+1 h(x)=2x+1,如何使用线性代数的知识表示 h ( x ) h(x) h(x)与 x x x之间的关系?
构建特征矩阵,添加系数全为1的1列,然后构建参数向量,1对应 θ 0 θ_0 θ0,2对应 θ 1 θ_1 θ1。x为特征数据,样本数据有 m m m个,此时 m = 3 m=3 m=3,分别对应 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3,保证截距没有其他系数干扰

矩阵与矩阵运算
对应位置进行运算。矩阵与向量不能直接进行相加运算。

矩阵与矩阵之间按位运算,并且形状要保持一致,否则不可运算。
有 3 ∗ 2 3*2 3∗2的矩阵与 2 ∗ 3 2*3 2∗3的矩阵进行相乘运算,可以把后面的 2 ∗ 3 2*3 2∗3的矩阵拆成3个向量进行计算,得到的是 3 ∗ 3 3*3 3∗3的矩阵。

n n n行 m m m列的矩阵乘以 m m m行 n n n列的矩阵,得到 n n n行 n n n列的矩阵。
例题:
某特征数据: [ 1 2 3 ] \begin{bmatrix} 1\\ 2\\3\end{bmatrix} 123 ,线性关系为: h ( x ) = 2 x + 1 h(x)=2x+1 h(x)=2x+1, h ( x ) = 3 x + 2 h(x)=3x+2 h(x)=3x+2,如何使用线性代数的知识表示 h ( x ) h(x) h(x)与 x x x之间的关系?

有多个 h ( x ) h(x) h(x)表现形式,把第一个线方程式中的1对应 θ 0 θ_0 θ0,2对应 θ 1 θ_1 θ1,第二个方程式中的2对应 θ 0 ′ θ_0' θ0′,3对应 θ 1 ′ θ_1' θ1′,多个方程式依次往后摆放。
单位矩阵
在自然数中,1乘以任何数等于任何数乘以1,等于任何数本身。单位矩阵对角线元素为1,其他元素全部为0,行列相同,也为方阵。
I = [ 1 0 0 0 1 0 0 0 1 ] I=\begin{bmatrix} 1&0&0\\ 0&1&0\\0&0&1\end{bmatrix} I= 100010001 , A ∗ I = I ∗ A = A A*I=I*A=A A∗I=I∗A=A
m ∗ m m*m m∗m单位矩阵乘以 m ∗ n m*n m∗n的矩阵,都为 m ∗ n m*n m∗n的矩阵,矩阵与单位矩阵相乘满足交换律,其他矩阵的计算并不满足交换律。
转置矩阵
把矩阵的行与列进行交换。

A i j = A j i T A_{ij}=A_{ji}^T Aij=AjiT
逆矩阵
只有 m ∗ m m*m m∗m的方阵才有逆矩阵,行列式不为0,逆矩阵的特点: A ∗ A − 1 = A − 1 ∗ A = I A*A^{-1}=A^{-1}*A=I A∗A−1=A−1∗A=I,好比 3 ∗ 3 − 1 = 1 3*3^{-1}=1 3∗3−1=1

多元线性回归
之前预测房价是通过一个特征(房子的大小)来预测的,而现实中影响房价的因素并不是只有房子的大小,还有很多其他特征在影响着房价,如北京的公寓价格要高于小城市的别墅等。这时考虑的特征不再只有1个,而是多个。当有多个特征来训练模型的时候,变量就会从 x 1 x_1 x1变为 x 1 . . . x n x_1...x_n x1...xn。
下图中有多少条记录,也就是有多少个样本数据集,标签就是目标值(价格),特征为:bedrooms,bathrooms,sqft_living,sqft_lot,floots,得出线性关系为: h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h(x)=θ_0+θ_1x_1+θ_2x_2+...+θ_nx_n h(x)=θ0+θ1x1+θ2x2+...+θnxn。

在公式中可以看成 x 0 = 1 x_0=1 x0=1,构建特征向量 x x x,参数向量 θ θ θ。有 m m m个数据样本集,向量 x x x的长度为 n + 1 n+1 n+1。

多元线性回归,多元就代表有多个参数,多个特征量或多个变量来预测 h ( x ) h(x) h(x),最终目的是求得一系列的 θ θ θ,使得代价函数最小。
公式: h ( x ) = θ T ∗ X = θ 0 x 0 + θ 1 x 1 + . . . + θ n x n h(x)=θ^T*X=θ_0x_0+θ_1x_1+...+θ_nx_n h(x)=θT∗X=θ0x0+θ1x1+...+θnxn
参数: θ 0 , θ 1 , . . . , θ n θ_0,θ_1,...,θ_n θ0,θ1,...,θn
代价函数: J ( θ 0 , θ 1 , . . . θ n ) = 1 2 m ∑ i = 1 m ( h ( x i ) − y i ) 2 J(θ_0,θ_1,...θ_n)= \frac{1}{2m}\displaystyle{\sum_{i=1}^{m}(h(x^i)-y^i)^2} J(θ0,θ1,...θn)=2m1i=1∑m(h(xi)−yi)2
目标:求得 θ 0 , θ 1 , . . . , θ n θ_0,θ_1,...,θ_n θ0,θ1,...,θn,使得代价函数最小
梯度下降法:拟定一个迭代次数,不停的对 θ θ θ求偏导,来更改或者迭代 θ θ θ参数,直到代价函数最小。
对 θ 0 θ_0 θ0求偏导, θ 0 θ_0 θ0为截距,从 θ 1 θ_1 θ1开始,后面的才为对应 x 1 x_1 x1前面的系数。

对 θ 1 θ_1 θ1求偏导。

对 θ 2 θ_2 θ2求偏导。


梯度下降法实现多元线性回归
货运公司送货,想根据历史数据实现一套预测总运输时间的模型。
运输里程、运输次数都是特征,总运输时间是标签(目标值),通过运输里程、运输次数来预测总运输时间。
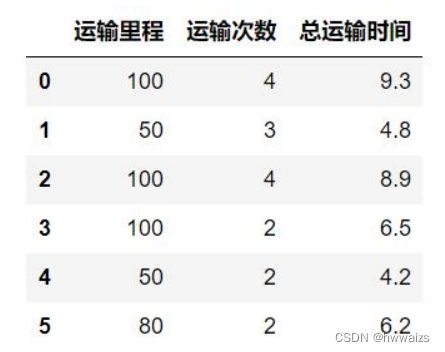


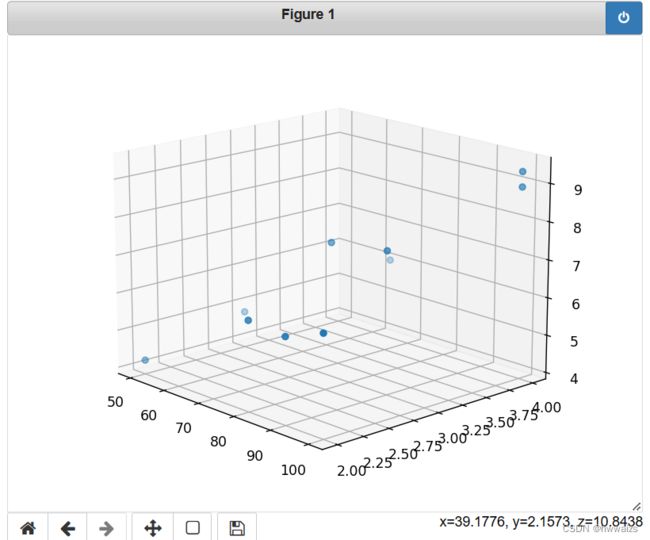


可以看到点分布在平面的上下,上下都有损失,总体来说在中间的位置,通过一个平面来拟合了两个特征的数据,可以得到预测的结果。
sklearn实现多元线性回归
代价函数最小的时候,求得的平面图。sklearn并不是梯度下降法封装的,用的是标准化方程。
多项式回归
假设房子的特征有两个:房子的宽度、长度,预测房价的方程: h ( x ) = θ 0 + θ 1 ∗ 宽 + θ 2 ∗ 长 h(x)=θ_0+θ_1*宽+θ_2*长 h(x)=θ0+θ1∗宽+θ2∗长,利用房子的面积公式可以把两个特征转化为一个,得到的公式为: h ( x ) = θ 0 + θ 1 ∗ 面积 h(x)=θ_0+θ_1*面积 h(x)=θ0+θ1∗面积。
有可视化的图形如下所示:
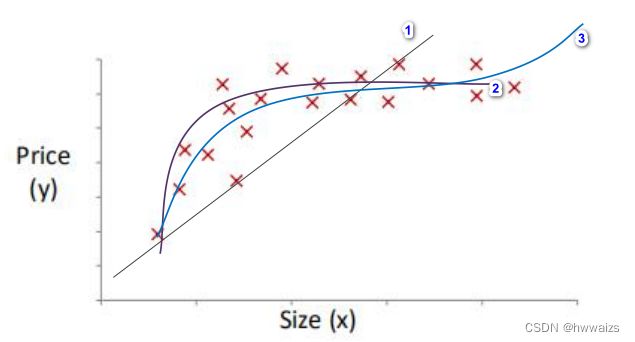
如果只有线性回归的话,拟合出一条向上的直线,所对应的方程: h ( x ) = θ 0 + θ 1 x h(x)=θ_0+θ_1x h(x)=θ0+θ1x。这条线对数据来说,并不是一条很好的拟合线,mse(损失)比较大。
如果用曲线进行拟合的话,得到的方程: h ( x ) = θ 0 + θ 1 x + θ 2 x 2 h(x)=θ_0+θ_1x+θ_2x^2 h(x)=θ0+θ1x+θ2x2,可以通过幂次来估计函数大致的走向,图形由幂次的高低决定,若曲线为抛物线,房价随着面积的增大而增大,到一定程度后,会随着房子面积的增大而减小,对于同一个地区并不会出现这种情况。
如果说要房价随着曲线由逐渐上升的趋势,就要引入高幂次,对应的方程: h ( x ) = θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 h(x)=θ_0+θ_1x+θ_2x^2+θ_3x^3 h(x)=θ0+θ1x+θ2x2+θ3x3。
涉及到了一元三次方程,可以通过替换的方法将高次幂变为低次幂。
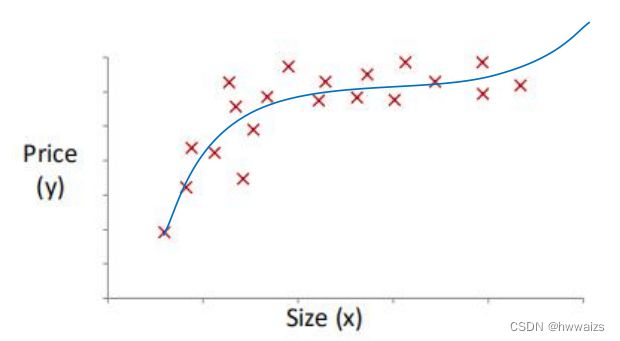
假设: x 1 = ( s i z e ) ; x 2 = ( s i z e ) 2 ; x 3 = ( s i z e ) 3 x_1=(size);x_2=(size)^2;x_3=(size)^3 x1=(size);x2=(size)2;x3=(size)3,转化为只有x一个特征,
h ( x ) = θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 = θ 0 + θ 1 ( s i z e ) + θ 2 ( s i z e ) 2 + θ 3 ( s i z e ) 3 = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 h(x)=θ_0+θ_1x+θ_2x^2+θ_3x^3=θ_0+θ_1(size)+θ_2(size)^2+θ_3(size)^3=θ_0+θ_1x_1+θ_2x_2+θ_3x_3 h(x)=θ0+θ1x+θ2x2+θ3x3=θ0+θ1(size)+θ2(size)2+θ3(size)3=θ0+θ1x1+θ2x2+θ3x3
将高幂次转化为多元线性回归的问题。
多项式回归案例
不同级别职位对应的薪水如下,建立级别薪资预测系统,通过传入新的level,来预测Salary。
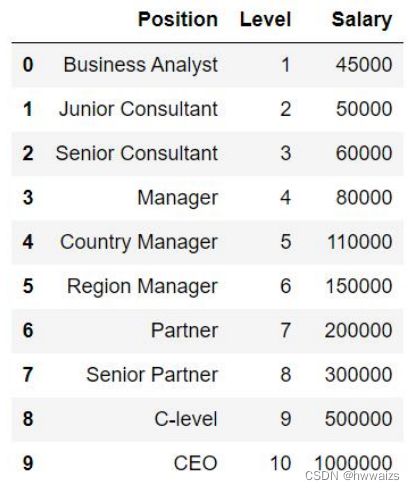
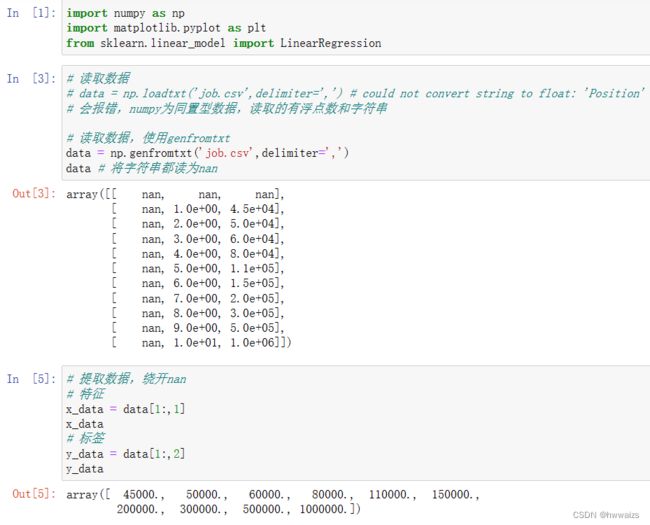

拟合的效果并不是很好,用多项式回归进行处理。


可以通过调整degree来改变拟合的程度。
标准方程法
梯度下降法是为了得到最小的代价函数 J ( θ ) J(θ) J(θ),求导 θ 0 , θ 1 , . . . , θ n θ_0,θ_1,...,θ_n θ0,θ1,...,θn,需要迭代很多次,才能收敛到全局的最小值。
标准方程法也可以求到全局的最小值,不再需要运用迭代算法,可以一次求得θ的最优值。 J ( θ ) = a θ 2 + b θ + c J(θ)=aθ^2+bθ+c J(θ)=aθ2+bθ+c,绘制的图形如下图所示:

选取合适的 θ θ θ找到方程的最小值,求最低点的 θ θ θ可以通过解方程、最低点的斜率是水平的为0,相当于在这个点求导,斜率为0,可以的得到, 2 a θ + b = 0 2aθ+b=0 2aθ+b=0, θ = − b 2 a θ=-\frac{b}{2a} θ=−2ab。
但是 θ θ θ通常为向量,所以代价函数为: J ( θ 0 , θ 1 , . . . , θ n ) = 1 2 m ∑ i = 1 m ( h ( x i ) − y i ) 2 J(θ_0,θ_1,...,θ_n)= \frac{1}{2m}{\displaystyle{\sum_{i=1}^{m}(h(x^i)-y^i)^2}} J(θ0,θ1,...,θn)=2m1i=1∑m(h(xi)−yi)2
如果需要用标准方程法去求解,就需要对每个 θ θ θ求偏导,并令结果为0。求解对应的 θ θ θ值。
标准方程法案例
之前用梯度下降法求解的时候,需要用两层for循环,造成代码的冗余。
J ( θ 0 , θ 1 , . . . , θ n ) = 1 2 m ∑ i = 1 m ( h ( x i ) − y i ) 2 J(θ_0,θ_1,...,θ_n)= \frac{1}{2m}{\displaystyle{\sum_{i=1}^{m}(h(x^i)-y^i)^2}} J(θ0,θ1,...,θn)=2m1i=1∑m(h(xi)−yi)2
该数据一共有4个训练样本,price为标签对应 y y y,特征有5个,为bedrooms,bathrooms,sqft_living,sqft_lot,floors,分布对应 x 1 − − x 5 x_1--x_5 x1−−x5,有多个特征数据,需要构建矩阵,添加上 x 0 x_0 x0,并使得其值全为1。

构成的矩阵为: X = [ 1 3 1.00 1185 5650 1.0 1 3 2.25 5270 7242 2.0 1 2 1.00 770 10000 1.0 1 4 3.00 1960 5000 1.0 ] X=\begin{bmatrix} 1&3&1.00&1185&5650&1.0\\ 1&3&2.25&5270&7242&2.0\\1&2&1.00&770&10000&1.0\\1&4&3.00&1960&5000&1.0\end{bmatrix} X= 111133241.002.251.003.00118552707701960565072421000050001.02.01.01.0
矩阵 X X X就是对应的特征矩阵。 y y y是真实值,构建的标签是向量, y = [ 221900 538000 180000 604000 ] y=\begin{bmatrix} 221900\\ 538000\\180000\\604000\end{bmatrix} y= 221900538000180000604000
θ = [ θ 0 θ 1 θ 2 θ 3 θ 4 θ 5 ] θ=\begin{bmatrix} θ_0\\ θ_1\\θ_2\\θ_3\\θ_4\\θ_5\end{bmatrix} θ= θ0θ1θ2θ3θ4θ5
利用 X , y , θ X,y,θ X,y,θ构建代价函数,先构建矩阵 X θ Xθ Xθ,其实也是 h ( x ) h(x) h(x)部分,误差值为真实值减去预测值, y − h ( x ) y-h(x) y−h(x),也即是 y − X θ y-Xθ y−Xθ。

求得的 e r r o r error error为单个的误差值,要得到误差的平方的求和,就转换为刚得到的误差向量乘以误差向量的转置。
如下图所示, e r r o r 0 = ( y − X θ ) error_0=(y-Xθ) error0=(y−Xθ), e r r o r 0 ∗ e r r o r 0 = ( y − X θ ) 2 error_0*error_0=(y-Xθ)^2 error0∗error0=(y−Xθ)2,误差向量与误差向量转置的乘积就为 ( y − X θ ) 2 (y-Xθ)^2 (y−Xθ)2。

求得最低值,也即是该点的斜率为0。求导过程如下,
逆矩阵乘以该矩阵 结果为单位矩阵。实现了标准方程法求 θ θ θ的方式。

标准方程法与梯度下降法的对比
标准方程法优点:求 θ θ θ值时,不需要选择学习率;不需要迭代,是两个向量之间直接做的运算替代了之前通过循环去控制每个样本数据的计算。缺点:需要计算逆矩阵,并不是所有的矩阵都有逆矩阵(方阵,行列不为0);当特征比较多的时候(n比较多),构建的是 ( n + 1 ) ∗ ( m + 1 ) (n+1)*(m+1) (n+1)∗(m+1)的矩阵,计算的时候,运算维度很高,所以特征变量非常多的时候,不太适合用标准方程法去求解。
梯度下降法优点:不需要计算逆矩阵,在特征量比较多的适合也适用。缺点:需要选择学习率;需要进行迭代。
数据量比较大(n的值是万以上级别)的适合用梯度下降法,特征向量比较小的时候用标准方程法。
numpy实现标准方程法求解
线性回归案例
有如下数据:“kc_house_data.csv”,我们需要对其进行模型的训练。
一元线性回归分析
查看数据的信息,样本21613条,21列,'id’房子的序号,'date’为数据采集的时间,对房价没有影响。'price’为标签,其余的均为特征。用一元线性回归的话,就取一个特征,如取住房面积"sqft_living"。

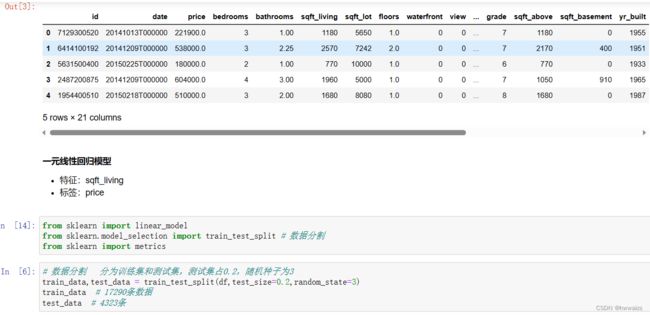


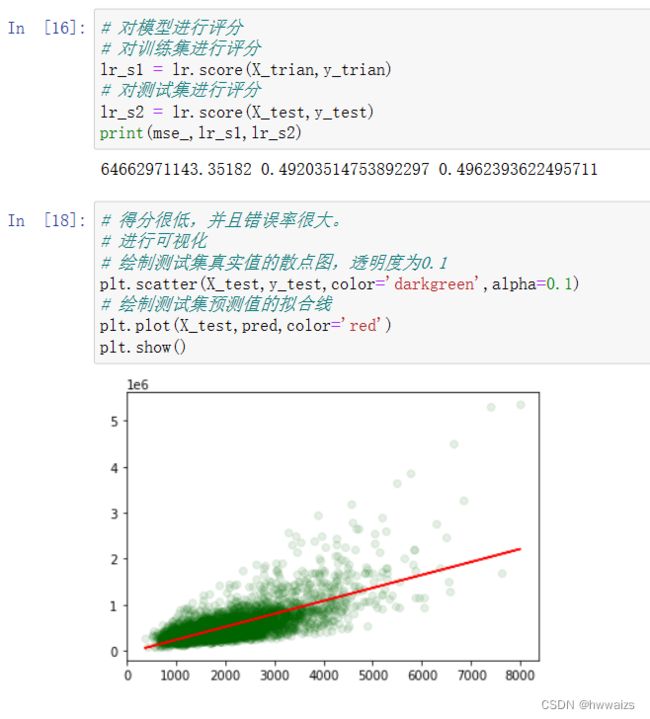
多元线性回归分析
特征有多个,标签只有1个"price",有多个特征在影响价格。

选出跟价格影响最大的一些特征去训练模型,可视化的形式显示出来。房间个数、楼层数、浴室个数跟房价的关系,房间个数不一定是连续的,绘制箱型图。

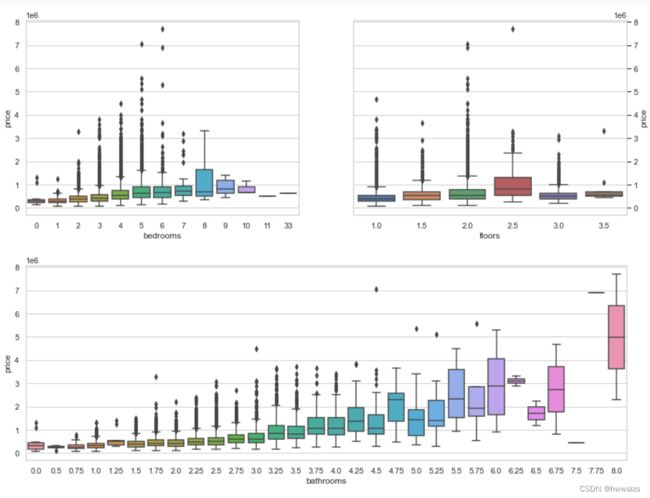
对得到的图形进行分析,当bedrooms 为11,33时,没有房价的分布,说明这两个是不需要的。房价在6以上的都可以去除掉,价格跟一些特征不是完全呈现线性关系,还需要考虑特征与特征之间的关系。


子图1跟子图2关系不大,子图3跟子图4存在关系,当房屋面积增大的时候,停车面积、房间个数、浴室个数都在增加,说明房屋面积跟停车面积、房间个数、浴室个数的相关性比较大;房屋面积跟楼层、房间个数没有多大的关系。用热力图绘制两两图形之间的关系。



当颜色非常淡的时候如-0.4,呈现负相关;当颜色非常绿的时候如0.6,呈现正相关,相关性比较紧密,自己与自己的相关性为1。住房面积"sqft_living"与price、bathrooms、grade、sqft_living15的关系比较紧密。如果只看正相关性强的,在特征选择上完全规避了一些不好的特征,模型训练出来就会过拟合。
选择特征的时候,注意:一是特征与标签之间的关系,一般要选择正相关的关系;二是要留一部分防止过拟合,三是剔除掉关系与关系之间特征性比较强的特征,如住房面积与15住房面积,不然会出现大量的计算。
特征与特征进行分析了后,进行多元线性回归模型的建立,特征不一样的时候,训练出来的结果也不一样。
多项式的处理

多项式训练出来的结果得分要强一些,预测出来的测试结果没有那么强,说明数据中有过拟合的现象。真实的结果没有训练出来的那么强。