算法图解注疏(待续)
目录
- 算法简介
-
- 二分查找
-
- 简单查找
- 更佳的查找方式
- 二分查找的几种模板
-
- 模板1
- 模板2
- 模板3
- 运行时间
- 大O表示法
-
- 大O表示法指出了最糟情况下的运行时间
- 一些常见的大O运行时间
- O(n!)旅行商问题
- 选择排序
-
- 内存的工作原理
- 数组和链表
- 选择排序
- 递归
-
- 基线条件和递归条件
- 栈
-
- 递归调用栈
- 快速排序
-
- 分而治之(divide and conquer,D&C)
- 快速排序
- 再谈大O表示法
算法简介
二分查找
二分查找是一种算法,其输入是一个有序的元素列表(必须有序的原因稍后解释)。如果要查找的元素包含在列表中,二分查找返回其位置;否则返回null
- 二分查找是一种在每次比较之后将查找空间一分为二的算法。
- 每次需要查找集合中的索引或元素时,都应该考虑二分查找。
- 如果集合是无序的,可以考虑先对其进行排序。
简单查找
下面的示例说明了二分查找的工作原理。我随便想一个1~100的数字,你的目标是以最少的次数猜到这个数字。你每次猜测后,我会说小了、大了或对了。
假设你从1开始依次往上猜,猜测过程会是这样:
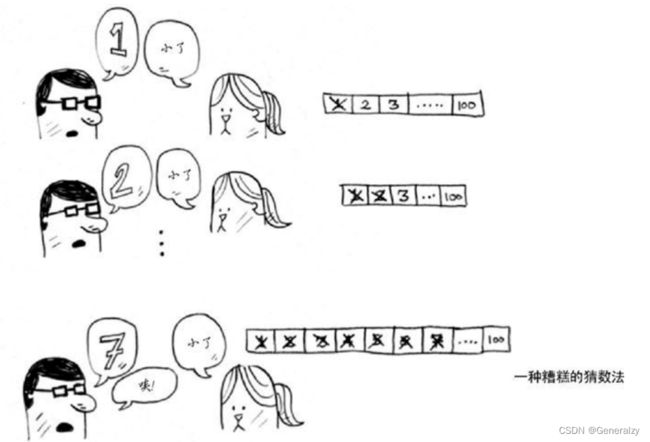
这是简单查找,更准确的说法是傻找。每次猜测都只能排除一个数字。如果我想的数字是99,你得猜99次才能猜到!
更佳的查找方式
下面是一种更佳的猜法。从50开始,
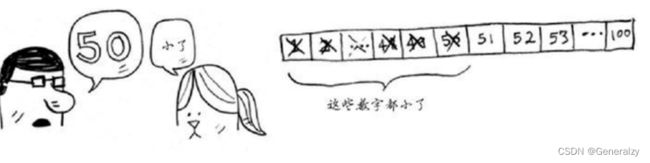
小了,但排除了一半的数字!至此,你知道1~50都小了。接下来,你猜75。
大了,那余下的数字又排除了一半!使用二分查找时,你猜测的是中间的数字,从而每次都将余下的数字排除一半。接下来,你猜63(50和75中间的数字)。
这就是二分查找!一般而言,对于包含n个元素的列表,用二分查找最多需要log2n步,而简单查找最多需要n步。
你可能不记得什么是对数了,但很可能记得什么是幂。log10100相当于问“将多少个10相乘的结果为100”。答案是两个:10 × 10 = 100。因此,log10100 = 2。对数运算是幂运算的逆运算。
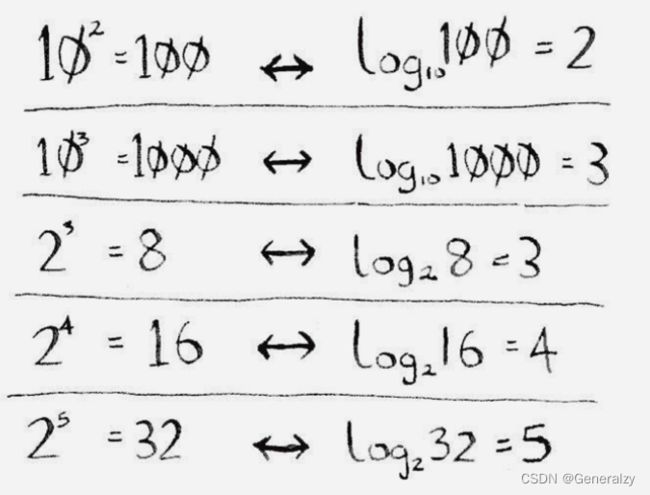
二分查找的几种模板
模板1
-
二分查找的最基础和最基本的形式。
-
查找条件可以在不与元素的两侧进行比较的情况下确定(或使用它周围的特定元素)。
-
不需要后处理,因为每一步中,你都在检查是否找到了元素。如果到达末尾,则知道未找到该元素。
-
模板特征:
初始条件:left = 0, right = length-1 终止: left > right 向左查找:right = mid-1 向右查找:left = mid+1
模板:
func search(nums []int, target int) int {
left :=0
right := len(nums)-1
for left<=right{
mid := (left+right)/2
if nums[mid]==target{
return mid
}else if nums[mid]>target{
right = mid-1
}else{
left = mid +1
}
}
return -1
}
以上的代码还可能会存在一个问题:溢出!
var left,right,mid uint8
left = 200;
right = 250;
//则left+right =450 > 255,此时已经溢出了
//0001 1100 0010 因为只能存储8位,实际1100 0010=194
mid = (left+right)/2; //此时实际mid=194/2
//此方法绝对不会溢出,最好写成这样
mid = left+(right-left)/2; //200+(250-200)/2 = 225
模板2
-
查找条件需要访问元素的直接右邻居。
-
使用元素的右邻居来确定是否满足条件,并决定是向左还是向右。
-
保证查找空间在每一步中至少有 2 个元素。
-
需要进行后处理。 当你剩下 1 个元素时,循环 / 递归结束。 需要评估剩余元素是否符合条件。
-
模板特征:
初始条件:left = 0, right = length 终止: left == right 向左查找:right = mid 向右查找:left = mid+1
模板:它用于查找需要访问数组中当前索引及其直接右邻居索引的元素或条件。
def binarySearch(nums, target):
if len(nums) == 0:
return -1
left, right = 0, len(nums)
while left < right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
elif nums[mid] < target:
left = mid + 1
else:
right = mid
# Post-processing:
# End Condition: left == right
if left != len(nums) and nums[left] == target:
return left
return -1
例题:寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
func findPeakElement(nums []int) int {
left:=0
right:=len(nums)-1
for left<right{
mid := left+(right-left)/2
if nums[mid]<nums[mid+1]{
left=mid+1
}else{
right=mid
}
}
return left
}
模板3
-
搜索条件需要访问元素的直接左右邻居。
-
使用元素的邻居来确定它是向右还是向左。
-
保证查找空间在每个步骤中至少有 3 个元素。
-
需要进行后处理。 当剩下 2 个元素时,循环 / 递归结束。 需要评估其余元素是否符合条件。
-
模板特征:
初始条件:left = 0, right = length-1 终止: left + 1 == right 向左查找:right = mid 向右查找:left = mid
模板:它用于搜索需要访问当前索引及其在数组中的直接左右邻居索引的元素或条件。
def binarySearch(nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
if len(nums) == 0:
return -1
left, right = 0, len(nums) - 1
while left + 1 < right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
elif nums[mid] < target:
left = mid
else:
right = mid
# Post-processing:
# End Condition: left + 1 == right
if nums[left] == target: return left
if nums[right] == target: return right
return -1
运行时间
一般而言,应选择效率最高的算法,以最大限度地减少运行时间或占用空间。
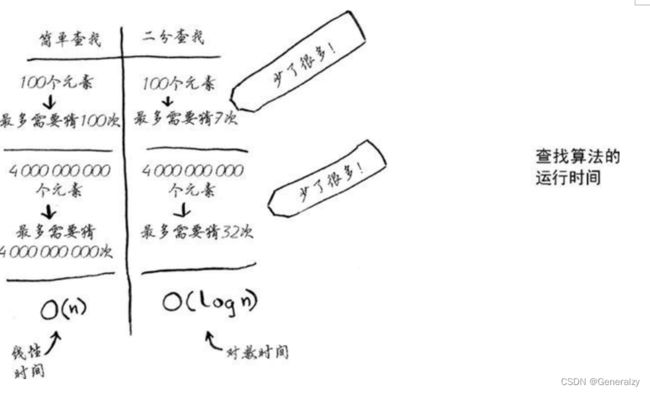
简单查找逐个地检查数字,如果列表包含100个数字,最多需要猜100次。如果列表包含40亿个数字,最多需要猜40亿次。换言之,最多需要猜测的次数与列表长度相同,这被称为线性时间(linear time)。
二分查找则不同。如果列表包含100个元素,最多要猜7次;如果列表包含40亿个数字,最多需猜32次。厉害吧?二分查找的运行时间为对数时间(或log时间)。
大O表示法
大O表示法指出了算法有多快。例如,假设列表包含n 个元素。简单查找需要检查每个元素,因此需要执行n 次操作。使用大O表示法,这个运行时间为O(n)。单位秒呢?没有——大O表示法指的并非以秒为单位的速度。大O表示法让你能够比较操作数,它指出了算法运行时间的增速。
为检查长度为n 的列表,二分查找需要执行log n 次操作。使用大O表示法,这个运行时间怎么表示呢?O(log n)。一般而言,大O表示法像下面这样。
大O表示法指出了最糟情况下的运行时间
假设你使用简单查找在电话簿中找人。你知道,简单查找的运行时间为O(n),这意味着在最糟情况下,必须查看电话簿中的每个条目。如果要查找的是Adit——电话簿中的第一个人,一次就能找到,无需查看每个条目。考虑到一次就找到了Adit,请问这种算法的运行时间是O(n)还是O(1)呢?
简单查找的运行时间总是为O(n)。查找Adit时,一次就找到了,这是最佳的情形,但大O表示法说的是最糟的情形。因此,你可以说,在最糟情况下,必须查看电话簿中的每个条目,对应的运行时间为O(n)。这是一个保证——你知道简单查找的运行时间不可能超过O(n)。
一些常见的大O运行时间
下面按从快到慢的顺序列出了经常会遇到的5种大O运行时间。
-
O(log n),也叫对数时间,这样的算法包括二分查找。
-
O(n),也叫线性时间,这样的算法包括简单查找。
-
O(n * log n),这样的算法包括快速排序——一种速度较快的排序算法。
-
O(n2),这样的算法包括选择排序——一种速度较慢的排序算法。
-
O(n!),这样的算法包括旅行商问题的解决方案——一种非常慢的算法。
假设你要绘制一个包含16格的网格,且有5种不同的算法可供选择,这些算法的运行时间如上所示。如果你选择第一种算法,绘制该网格所需的操作数将为4(log 16 = 4)。假设你每秒可执行10次操作,那么绘制该网格需要0.4秒。如果要绘制一个包含1024格的网格呢?这需要执行10(log 1024 = 10)次操作,换言之,绘制这样的网格需要1秒。这是使用第一种算法的情况。
第二种算法更慢,其运行时间为O(n)。即要绘制16个格子,需要执行16次操作;要绘制1024个格子,需要执行1024次操作。执行这些操作需要多少秒呢?
下面按从快到慢的顺序列出了使用这些算法绘制网格所需的时间:

实际上,并不能如此干净利索地将大O运行时间转换为操作数,但就目前而言,这种准确度足够了当前,我们获得的主要启示如下:
-
算法的速度指的并非时间,而是操作数的增速。
-
谈论算法的速度时,说的是随着输入的增加,其运行时间将以什么样的速度增加。
-
算法的运行时间用大O表示法表示。
-
O(log n)比O(n)快,当需要搜索的元素越多时,前者比后者快得越多。
O(n!)旅行商问题
这位旅行商(姑且称之为Opus吧)要前往这5个城市,同时要确保旅程最短。为此,可考虑前往这些城市的各种可能顺序。
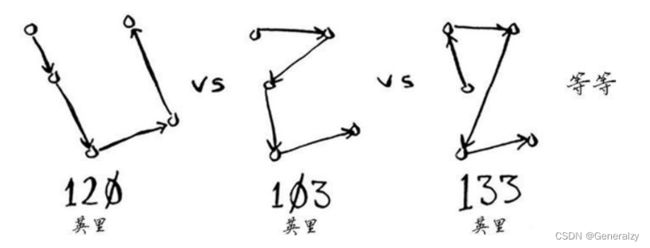
对于每种顺序,他都计算总旅程,再挑选出旅程最短的路线。5个城市有120种不同的排列方式。因此,在涉及5个城市时,解决这个问题需要执行120次操作。涉及6个城市时,需要执行720次操作(有720种不同的排列方式)。涉及7个城市时,需要执行5040次操作!
推而广之,涉及n个城市时,需要执行n!(n的阶乘)次操作才能计算出结果。因此运行时间为O(n!),即阶乘时间。除非涉及的城市数很少,否则需要执行非常多的操作。如果涉及的城市数超过100,根本就不能在合理的时间内计算出结果——等你计算出结果,太阳都没了。
这种算法很糟糕!Opus应使用别的算法,可他别无选择。这是计算机科学领域待解的问题之一。对于这个问题,目前还没有找到更快的算法,有些很聪明的人认为这个问题根本就没有更巧妙的算法。
选择排序
内存的工作原理
假设你去看演出,需要将东西寄存。寄存处有一个柜子,柜子有很多抽屉。每个抽屉可放一样东西,你有两样东西要寄存,因此要了两个抽屉。在你可以去看演出了!这大致就是计算机内存的工作原理。计算机就像是很多抽屉的集合体,每个抽屉都有地址。
需要将数据存储到内存时,你请求计算机提供存储空间,计算机给你一个存储地址。需要存储多项数据时,有两种基本方式——数组和链表。但它们并非都适用于所有的情形,因此知道它们的差别很重要。
数组和链表
有时候,需要在内存中存储一系列元素。假设你要编写一个管理待办事项的应用程序,为此需要将这些待办事项存储在内存中。鉴于数组更容易掌握,我们先将待办事项存储在数组中。使用数组意味着所有待办事项在内存中都是相连的(紧靠在一起的)。
现在假设你要添加第四个待办事项,但后面的那个抽屉放着别人的东西!
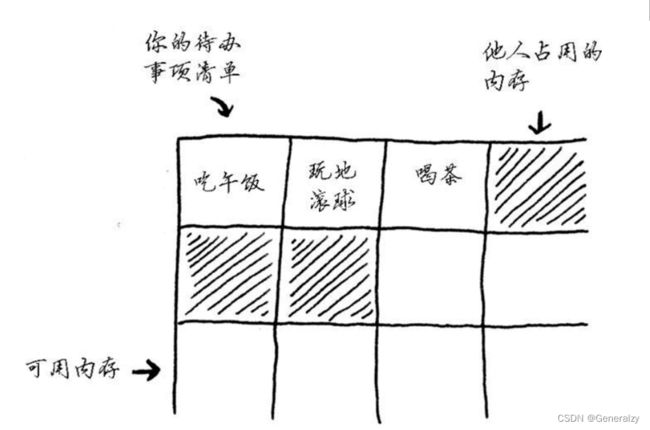
在这种情况下,你需要请求计算机重新分配一块可容纳4个待办事项的内存,再将所有待办事项都移到那里。
因此添加新元素的速度会很慢。一种解决之道是“预留座位”:即便当前只有3个待办事项,也请计算机提供10个位置,以防需要添加待办事项。这样,只要待办事项不超过10个,就无需转移。这是一个不错的权变措施,但你应该明白,它存在如下两个缺点。
-
你额外请求的位置可能根本用不上,这将浪费内存。你没有使用,别人也用不了。
-
待办事项超过10个后,你还得转移。
因此,这种权宜措施虽然不错,但绝非完美的解决方案。对于这种问题,可使用链表来解决。
————————————————————————————————————————————
链表中的元素可存储在内存的任何地方。
链表的每个元素都存储了下一个元素的地址,从而使一系列随机的内存地址串在一起。
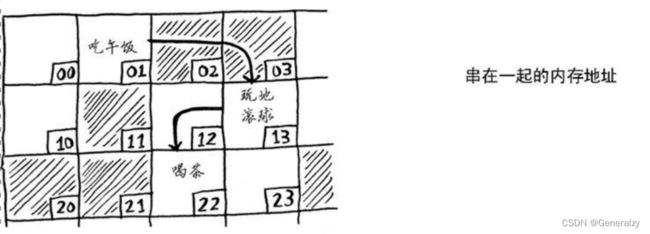
在需要读取链表的最后一个元素时,你不能直接读取,因为你不知道它所处的地址,必须先访问元素#1,从中获取元素#2的地址,再访问元素#2并从中获取元素#3的地址,以此类推,直到访问最后一个元素。需要同时读取所有元素时,链表的效率很高:你读取第一个元素,根据其中的地址再读取第二个元素,以此类推。但如果你需要跳跃,链表的效率真的很低。
数组与此不同:你知道其中每个元素的地址。例如,假设有一个数组,它包含五个元素,起始地址为00,那么元素#5的地址是多少呢?
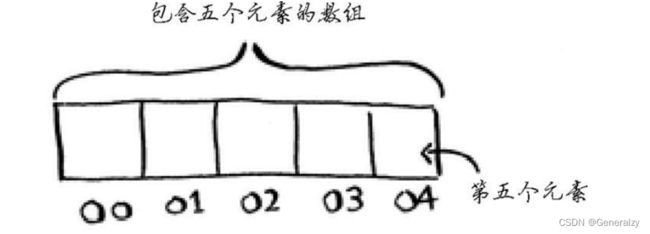
只需执行简单的数学运算就知道:04。需要随机地读取元素时,数组的效率很高,因为可迅速找到数组的任何元素。在链表中,元素并非靠在一起的,你无法迅速计算出第五个元素的内存地址,而必须先访问第一个元素以获取第二个元素的地址,再访问第二个元素以获取第三个元素的地址,以此类推,直到访问第五个元素。
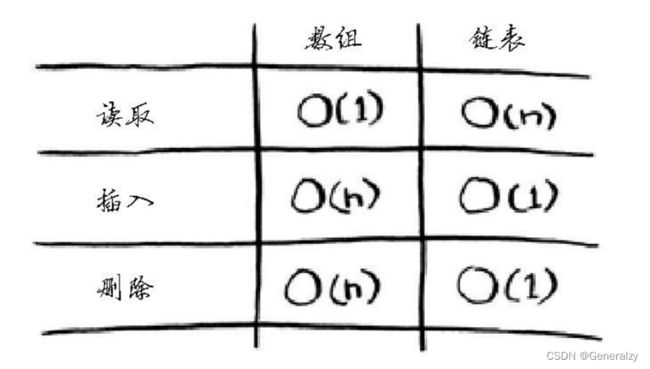
下面列出了常见的数组和链表操作的运行时间。
数组和链表哪个用得更多呢?显然要看情况。但数组用得很多,因为它支持随机访问。有两种访问方式:随机访问和顺序访问。顺序访问意味着从第一个元素开始逐个地读取元素。链表只能顺序访问:要读取链表的第十个元素,得先读取前九个元素,并沿链接找到第十个元素。随机访问意味着可直接跳到第十个元素。
选择排序
假设你的计算机存储了很多乐曲。对于每个乐队,你都记录了其作品被播放的次数。

你要将这个列表按播放次数从多到少的顺序排列,从而将你喜欢的乐队排序。该如何做呢?
一种办法是遍历这个列表,找出作品播放次数最多的乐队,并将该乐队添加到一个新列表中。
要找出播放次数最多的乐队,必须检查列表中的每个元素。这需要的时间为O(n)。因此对于这种时间为O(n)的操作,你需要执行n次。
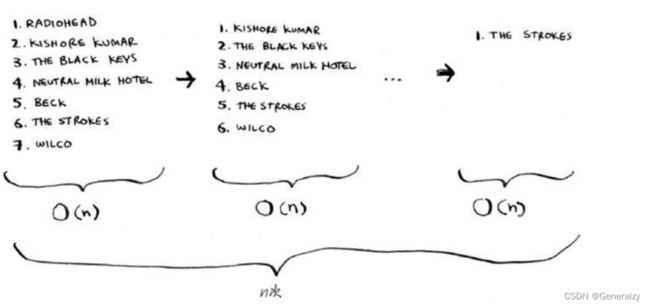
需要的总时间为 O(n × n),即O(n2)。
选择排序是一种灵巧的算法,但其速度不是很快。快速排序是一种更快的排序算法,其运行时间为O(n log n)。
func selectorSort(nums []int) {
length := len(nums)
for index := 0; index < length-1; index++ {
for ptr := index + 1; ptr < length; ptr++ {
if nums[ptr] < nums[index] {
nums[ptr], nums[index] = nums[index], nums[ptr]
}
}
}
}
递归
假设你在祖母的阁楼中翻箱倒柜,发现了一个上锁的神秘手提箱。祖母告诉你,钥匙很可能在下面这个盒子里。
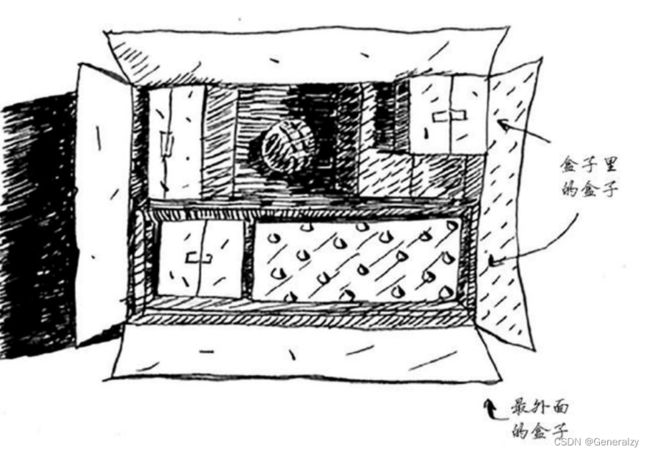
这个盒子里有盒子,而盒子里的盒子又有盒子。钥匙就在某个盒子中。为找到钥匙,你将使用什么算法?
下面是一种方法。
(2) 从盒子堆取出一个盒子,在里面找。
(3) 如果找到的是盒子,就将其加入盒子堆中,以便以后再查找。
(4) 如果找到钥匙,则大功告成!
(5) 回到第二步。
(2) 如果是盒子,就回到第一步。
(3) 如果是钥匙,就大功告成!
第一种方法使用的是while循环:只要盒子堆不空,就从中取一个盒子,并在其中仔细查找。伪代码如下:
第二种方法使用递归——函数调用自己,这种方法的伪代码如下。
def look_for_key(box):
for item in box:
if item.is_a_box():
look_for_key(item) ←------递归!
elif item.is_a_key():
print "found the key!"
这两种方法的作用相同,第二种方法更清晰。递归只是让解决方案更清晰,并没有性能上的优势。实际上,在有些情况下,使用循环的性能更好。
基线条件和递归条件
由于递归函数调用自己,因此编写这样的函数时很容易出错,进而导致无限循环。
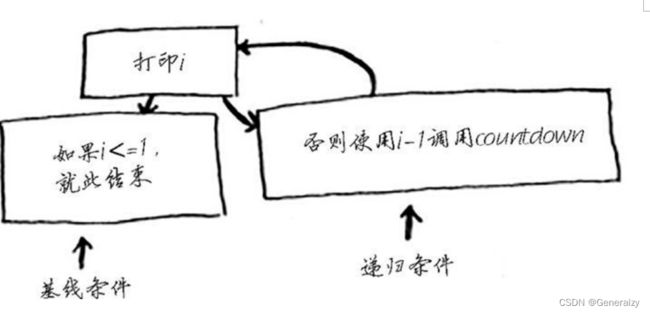
编写递归函数时,必须告诉它何时停止递归。正因为如此,每个递归函数都有两部分:基线条件(base case)和递归条件(recursive case)。递归条件指的是函数调用自己,而基线条件则指的是函数不再调用自己,从而避免形成无限循环。
栈
调用栈不仅对编程来说很重要,使用递归时也必须理解这个概念。
假设你去野外烧烤,并为此创建了一个待办事项清单——一叠便条。
一叠便条要简单得多:插入的待办事项放在清单的最前面;读取待办事项时,你只读取最上面的那个,并将其删除。因此这个待办事项清单只有两种操作:压入(插入)和弹出(删除并读取)。
计算机在内部使用被称为调用栈的栈。我们来看看计算机是如何使用调用栈的。下面是一个简单的函数。这个函数问候用户,再调用另外两个函数。这两个函数的代码如下。
def greet(name):
print "hello, " + name + "!"
greet2(name)
print "getting ready to say bye..."
bye()
def greet2(name):
print "how are you, " + name + "?"
def bye():
print "ok bye!"
假设你调用greet(“maggie”),计算机将首先为该函数调用分配一块内存。变量name被设置为maggie,这需要存储到内存中。

每当你调用函数时,计算机都像这样将函数调用涉及的所有变量的值存储到内存中。接下来,你打印hello, maggie!,再调用greet2(“maggie”)。同样,计算机也为这个函数调用分配一块内存。
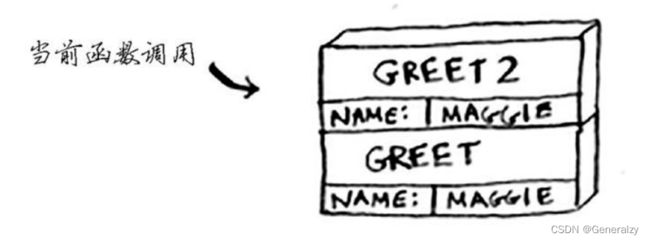
计算机使用一个栈来表示这些内存块,其中第二个内存块位于第一个内存块上面。你打印how are you, maggie?,然后从函数调用返回。此时,栈顶的内存块被弹出。
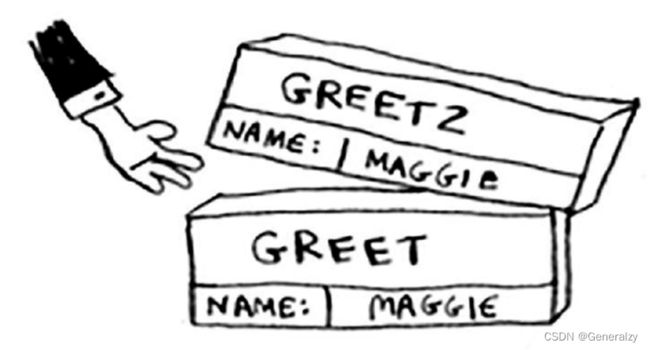
现在,栈顶的内存块是函数greet的,这意味着你返回到了函数greet。当你调用函数greet2时,函数greet只执行了一部分。这是一个重要概念:调用另一个函数时,当前函数暂停并处于未完成状态。该函数的所有变量的值都还在内存中。执行完函数greet2后,你回到函数greet,并从离开的地方开始接着往下执行:首先打印getting ready to say bye.,再调用函数bye。

在栈顶添加了函数bye的内存块。然后,你打印ok bye!,并从这个函数返回。

现在你又回到了函数greet。由于没有别的事情要做,你就从函数greet返回。这个栈用于存储多个函数的变量,被称为调用栈。
递归调用栈
递归函数也使用调用栈!来看看递归函数factorial的调用栈。factorial(5)写作5!,其定义如下:5! = 5 * 4 * 3 * 2 * 1。同理,factorial(3)为3 * 2 * 1。下面是计算阶乘的递归函数。
def fact(x):
if x == 1:
return 1 else:
return x * fact(x-1)
下面来详细分析调用fact(3)时调用栈是如何变化的。
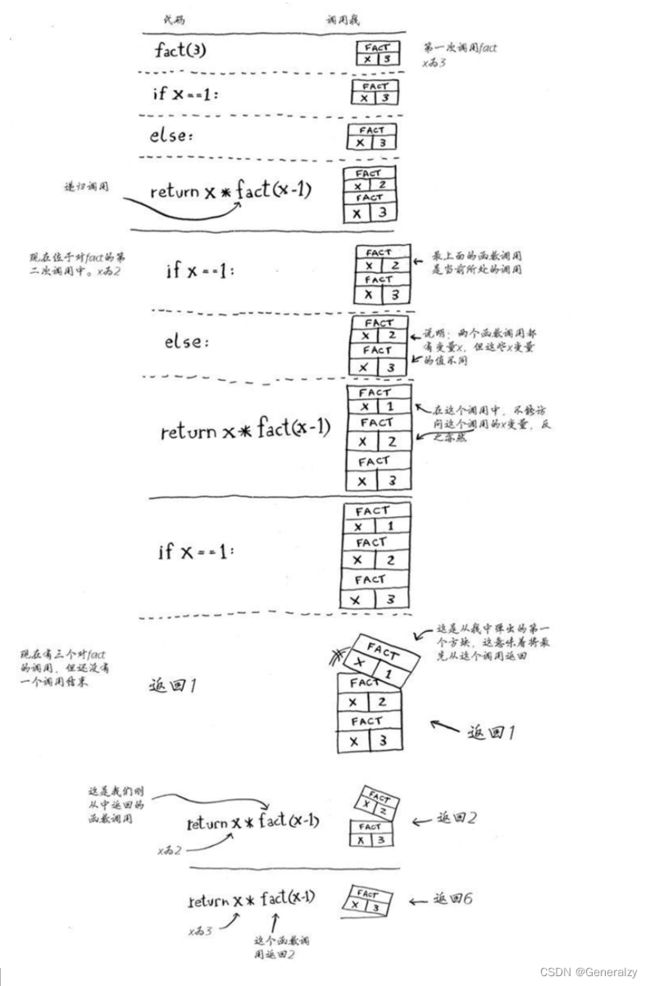
注意,每个fact调用都有自己的x变量。在一个函数调用中不能访问另一个的x变量。
-
每个递归函数都有两个条件:基线条件和递归条件。
-
栈有两种操作:压入和弹出。
-
所有函数调用都进入调用栈。
-
调用栈可能很长,这将占用大量的内存。
快速排序
分而治之(divide and conquer,D&C)
D&C并不那么容易掌握,将通过示例来介绍。首先,介绍一个直观的示例;
假设你是农场主,有一小块土地。你要将这块地均匀地分成方块,且分出的方块要尽可能大。显然,下面的分法都不符合要求。
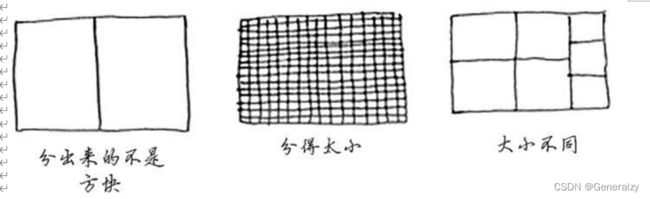
如何将一块地均匀地分成方块,并确保分出的方块是最大的呢?使用D&C策略!D&C算法是递归的。使用D&C解决问题的过程包括两个步骤。
(1) 找出基线条件,这种条件必须尽可能简单。
(2) 不断将问题分解(或者说缩小规模),直到符合基线条件。
下面就来使用D&C找出前述问题的解决方案。可你能使用的最大方块有多大呢?
首先,找出基线条件。最容易处理的情况是,一条边的长度是另一条边的整数倍。
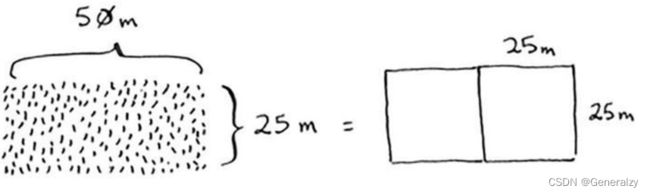
如果一边长25 m,另一边长50 m,那么可使用的最大方块为 25 m×25 m。换言之,可以将这块地分成两个这样的方块。
现在需要找出递归条件,这正是D&C的用武之地。根据D&C的定义,每次递归调用都必须缩小问题的规模。如何缩小前述问题的规模呢?我们首先找出这块地可容纳的最大方块。
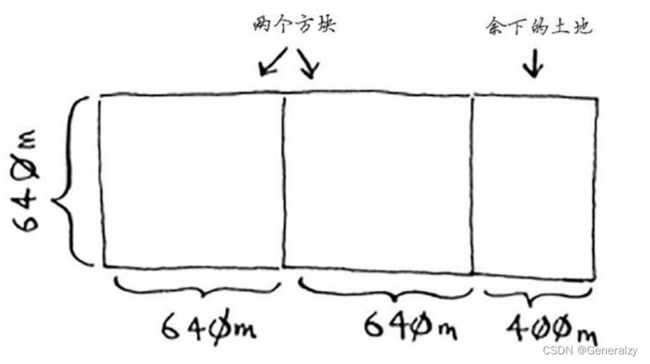
你可以从这块地中划出两个640 m×640 m的方块,同时余下一小块地。现在是顿悟时刻:何不对余下的那一小块地使用相同的算法呢?
最初要划分的土地尺寸为1680 m×640 m,而现在要划分的土地更小,为640 m×400 m。适用于这小块地的最大方块,也是适用于整块地的最大方块。换言之,你将均匀划分1680 m×640 m土地的问题,简化成了均匀划分640 m×400 m土地的问题!对于640 m × 400 m的土地,可从中划出的最大方块为400 m × 400 m。
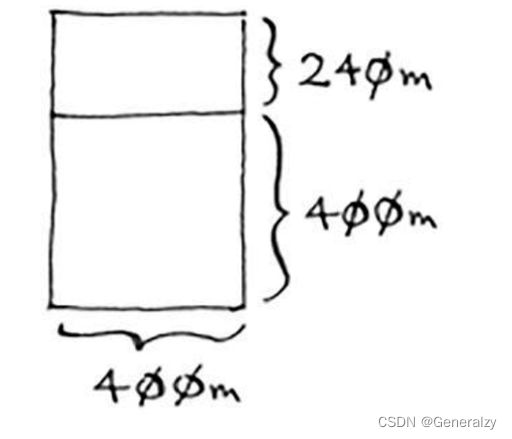
这将余下一块更小的土地,其尺寸为400 m × 240 m。你可从这块土地中划出最大的方块,余下一块更小的土地,其尺寸为240 m × 160 m。接下来,从这块土地中划出最大的方块,余下一块更小的土地。余下的这块土地满足基线条件,因为160是80的整数倍。将这块土地分成两个方块后,将不会余下任何土地!
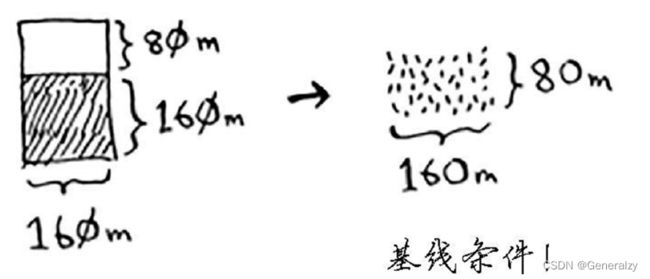
因此,对于最初的那片土地,适用的最大方块为80 m× 80 m。
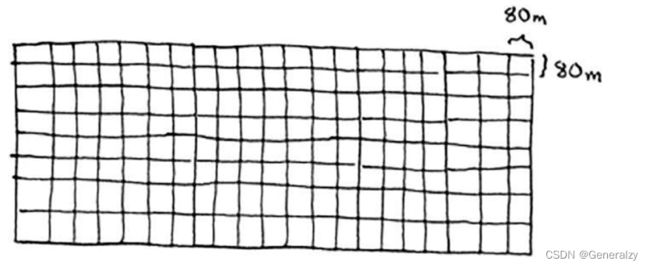
这里重申一下D&C的工作原理:
(1) 找出简单的基线条件;
(2) 确定如何缩小问题的规模,使其符合基线条件。
D&C并非可用于解决问题的算法,而是一种解决问题的思路。
再来看一个例子。给定一个数字数组。你需要将这些数字相加,并返回结果。使用循环很容易完成这种任务。但如何使用递归函数来完成这种任务呢?
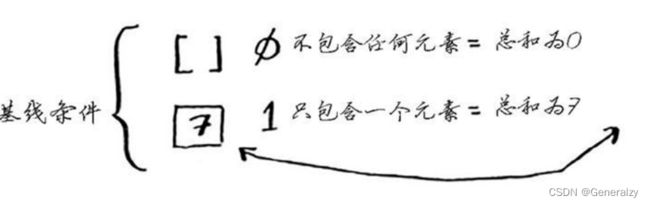
第一步:找出基线条件。最简单的数组什么样呢?请想想这个问题,再接着往下读。如果数组不包含任何元素或只包含一个元素,计算总和将非常容易。
第二步:每次递归调用都必须离空数组更近一步。如何缩小问题的规模呢?下面是一种办法。

函数sum的工作原理类似于下面这样。
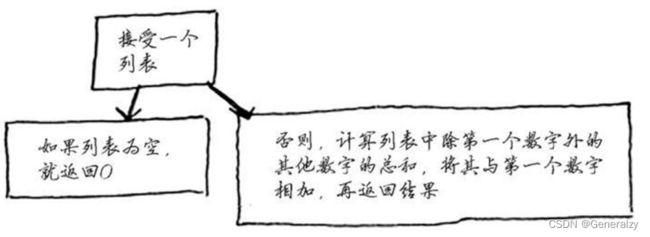
这个函数的运行过程如下。

快速排序
快速排序是一种常用的排序算法,比选择排序快得多。例如,C语言标准库中的函数qsort实现的就是快速排序。快速排序也使用了D&C。
下面来使用快速排序对数组进行排序。对排序算法来说,最简单的数组什么样呢?还记得前一节的“提示”吗?就是根本不需要排序的数组。

因此,基线条件为数组为空或只包含一个元素。在这种情况下,只需原样返回数组——根本就不用排序。
def quicksort(array):
if len(array) < 2:
return array
我们来看看更长的数组。对包含两个元素的数组进行排序也很容易,检查第二个元素是否比第一个元素小,小就交换位置。

包含三个元素的数组呢?要使用D&C,因此需要将数组分解,直到满足基线条件。下面介绍快速排序的工作原理。首先,从数组中选择一个元素,这个元素被称为基准值(pivot)。
稍后再介绍如何选择合适的基准值。我们暂时将数组的第一个元素用作基准值。接下来,找出比基准值小的元素以及比基准值大的元素。
- 一个由所有小于基准值的数字组成的子数组;基准值;
- 一个由所有大于基准值的数组组成的子数组。
这里只是进行了分区,得到的两个子数组是无序的。但如果这两个数组是有序的,对整个数组进行排序将非常容易。
如何对子数组进行排序呢?对于包含两个元素的数组(左边的子数组)以及空数组(右边的子数组),快速排序知道如何将它们排序,因此只要对这两个子数组进行快速排序,再合并结果,就能得到一个有序数
quicksort([15, 10]) + [33] + quicksort([])
刚才你大致见识了归纳证明!归纳证明是一种证明算法行之有效的方式,它分两步:基线条件和归纳条件。是不是有点似曾相识的感觉?例如,假设我要证明我能爬到梯子的最上面。归纳条件是这样的:如果我站在一个横档上,就能将脚放到上面一个横档上。换言之,如果我站在第二个横档上,就能爬到第三个横档。这就是归纳条件。而基线条件是这样的,即我已经站在第一个横档上。因此,通过每次爬一个横档,我就能爬到梯子最顶端。
对于快速排序,可使用类似的推理。在基线条件中,我证明这种算法对空数组或包含一个元素的数组管用。在归纳条件中,我证明如果快速排序对包含一个元素的数组管用,对包含两个元素的数组也将管用;如果它对包含两个元素的数组管用,对包含三个元素的数组也将管用,以此类推。因此,我可以说,快速排序对任何长度的数组都管用。这里不再深入讨论归纳证明,但它很有趣,并与D&C协同发挥作用。
下面是快速排序的代码。
def quicksort(array):
if len(array) < 2:
return array ←------基线条件:为空或只包含一个元素的数组是“有序”的else:
pivot = array[0] ←------递归条件
less = [i for i in array[1:] if i <= pivot] ←------由所有小于等于基准值的
greater = [i for i in array[1:] if i > pivot] ←------由所有大于基准值的
return quicksort(less) + [pivot] + quicksort(greater)
print quicksort([10, 5, 2, 3])
这段代码是一个递归实现的快速排序算法。它使用了 Python 语言来实现快速排序,并且采用了一种相对简洁的递归写法。虽然在代码形式上与传统的快速排序实现有所不同,但本质上仍然是一个快速排序算法,具有相同的时间复杂度。
让我们来详细解释这段代码的逻辑:
-
首先,定义了一个
quicksort函数,该函数接受一个列表array作为输入。 -
在
quicksort函数中,首先检查列表array的长度,如果长度小于 2,即为空或只包含一个元素,那么该列表已经是有序的,直接返回该列表。 -
如果列表长度大于等于 2,则进行递归排序:
a. 首先,选择列表中的第一个元素
pivot作为基准值(也可以是其他选择,但这里选择的是第一个元素)。b. 创建两个新列表
less和greater,用来存放比基准值小于等于和大于的元素。c. 使用列表解析生成
less和greater列表:less中包含所有小于等于基准值的元素,而greater中包含所有大于基准值的元素。d. 对
less和greater两个列表分别递归调用quicksort函数,对它们进行排序。e. 最后,将
less列表、基准值pivot和greater列表拼接在一起,形成最终的有序列表,并返回。 -
在
print语句中,调用quicksort函数并传入[10, 5, 2, 3]作为输入,然后打印排序后的结果。
这段代码使用了递归来不断划分子列表并排序,直到达到基线条件(列表长度小于 2),从而完成整个快速排序过程。虽然在传统的快速排序实现中,可能会使用原地排序和分区技巧,但这个实现依然是一个有效的快速排序算法。
再给出第二种快排方式:
def partition(li, left, right):
"""
归位操作
:param li: 列表
:param left: 左边下标
:param right: 右边下标
:return:
"""
tmp = li[left]
while left < right:
while left < right and li[right] >= tmp: # 在右边找比tmp小的
right -= 1
li[left] = li[right] # 把右边的值写到左边
print(li, 'right')
while left < right and li[left] <= tmp: # 在左边找比tmp大的
left += 1
li[right] = li[left] # 把左边的值写到右边
print(li, 'left')
li[left] = tmp # 把tmp归位
return left
def quick_sort(li, left, right):
"""
快排
:param li: 列表
:param left: 左边下标
:param right: 右边下标
:return:
"""
if left < right:
mid = partition(li, left, right)
quick_sort(li, left, mid - 1)
quick_sort(li, mid + 1, right)
这段代码是另一种快速排序实现方式,与之前的递归实现方式相比,它采用了一种基于指针的原地排序方法。这种实现方式通常称为“Hoare Partition”的快速排序。
主要区别在于如何进行分区(Partition)操作:
-
Hoare Partition:
-
分区函数
partition(li, left, right)用于将列表li的子区间[left, right]进行分区操作,将小于等于基准值tmp的元素移到左边,大于基准值的元素移到右边,并返回基准值的索引位置。 -
在
partition函数中,使用两个指针left和right分别从区间的左右两端开始遍历,不断找到需要交换的元素,然后进行交换,直到两个指针相遇。 -
该方法在进行分区操作时,可能会产生两侧的子区间不平衡,即某一侧可能比较短,可能导致快速排序的效率下降。为了解决这个问题,
partition函数返回的基准值索引位置不是固定的中间位置,而是根据实际情况得出的。
-
-
递归快速排序:
-
快速排序函数
quick_sort(li, left, right)采用递归方式进行快速排序。 -
在
quick_sort函数中,先调用partition函数将列表分为两个子区间,然后对两个子区间分别递归调用quick_sort函数进行排序。
-
不同之处在于实现细节和分区方法,而核心思想都是快速排序。partition 函数负责将列表进行分区,quick_sort 函数负责递归调用实现排序过程。这种 Hoare Partition 的快速排序在实际中也是常用且高效的排序算法。
再谈大O表示法
快速排序的独特之处在于,其速度取决于选择的基准值。在讨论快速排
序的运行时间前,我们再来看看最常见的大O运行时间。
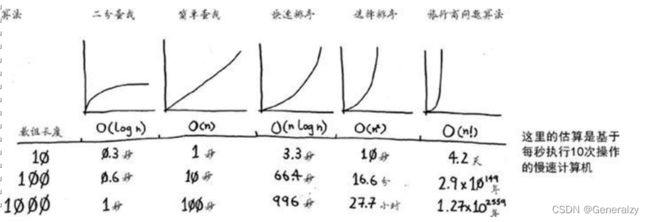
上述图表中的时间是基于每秒执行10次操作计算得到的。这些数据并不准确,这里提供它们只是想让你对这些运行时间的差别有大致认识。实际上,计算机每秒执行的操作远不止10次。
平均情况和最糟情况
快速排序的性能高度依赖于你选择的基准值。假设你总是将第一个元素用作基准值,且要处理的数组是有序的。由于快速排序算法不检查输入数组是否有序,因此它依然尝试对其进行排序。
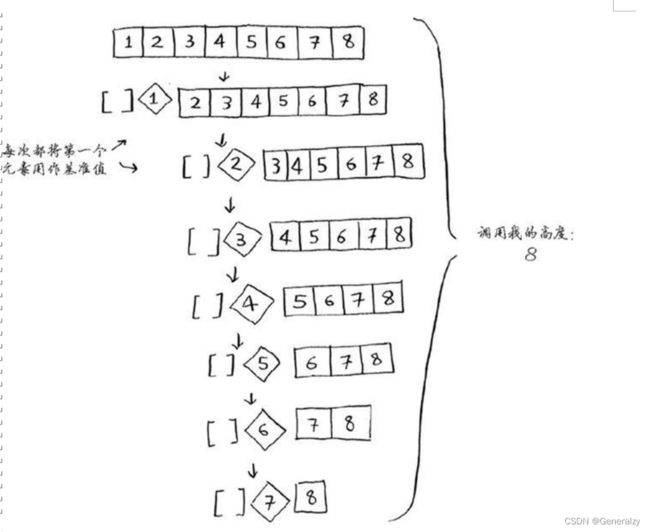
注意,数组并没有被分成两半,相反,其中一个子数组始终为空,这导致调用栈非常长。现在假设你总是将中间的元素用作基准值,在这种情况下,调用栈如下。
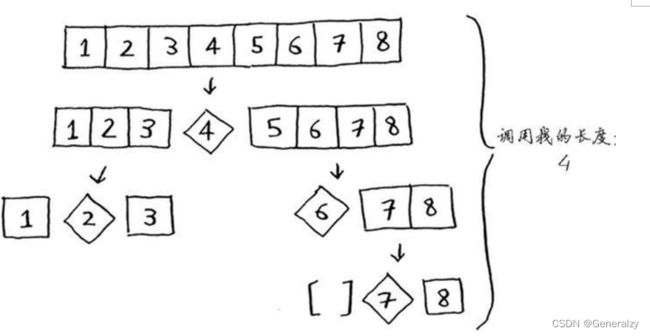
调用栈短得多!因为你每次都将数组分成两半,所以不需要那么多递归调用。你很快就到达了基线条件,因此调用栈短得多。
第一个示例展示的是最糟情况,而第二个示例展示的是最佳情况。在最糟情况下,栈长为O(n),而在最佳情况下,栈长为O(log n)。
现在来看看栈的第一层。你将一个元素用作基准值,并将其他的元素划分到两个子数组中。这涉及数组中的全部8个元素,因此该操作的时间为O(n)。在调用栈的第一层,涉及全部8个元素,但实际上,在调用栈的每层都涉及O(n)个元素。
即便以不同的方式划分数组,每次也将涉及O(n)个元素。因此,完成每层所需的时间都为O(n)。
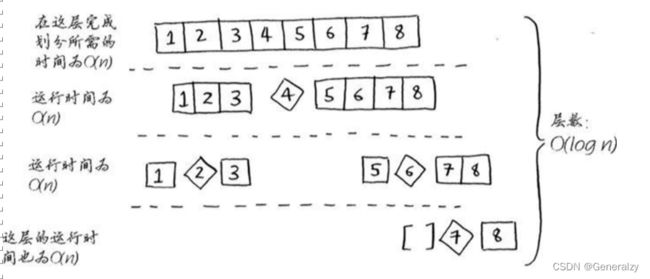
在这个示例中,层数为O(log n)(用技术术语说,调用栈的高度为O(log n)),而每层需要的时间为O(n)。因此整个算法需要的时间为O(n) * O(log n) = O(n log n)。这就是最佳情况。
在最糟情况下,有O(n)层,因此该算法的运行时间为O(n) * O(n) = O(n2)。
最佳情况也是平均情况。只要你每次都随机地选择一个数组元素作为基准值,快速排序的平均运行时间就将
为O(n log n)。快速排序是最快的排序算法之一,也是D&C典范。