【C++】AVL树的实现及测试
文章目录
- AVL树节点的定义
- AVL树的定义
- AVL树的插入
- 插入后更新平衡因子
- AVL树的右单旋
- AVL树的左单旋
- 先左单旋再右单旋
- 先右单旋再左单旋
- 检查是否满足AVL树
- 总代码
AVL树
AVL树也叫平衡二叉搜索树,通过旋转解决了搜索二叉树的不确定性,让整颗树趋近于一颗满二叉树。
1.左右都是一颗AVL树
2.平衡因子的绝对值不会超过1
上图的蓝字表示平衡因子,平衡因子=右子树的高度-左子树的高度
AVL树节点的定义
template
struct AVLTreeNode
{
ALVTreeNode* _left;
AVLTreeNode* _right;
AVLTreeNode* _parent;//父亲节点
pair _kv;// key / value
//构造函数
AVLTreeNode(const pair& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{}
int _bf;//平衡因子
};
AVL树的定义
template
class AVLTree
{
typedef AVLTreeNode Node;
public:
private:
Node* _root=nullptr;
};
AVL树的插入
AVL树的插入和二叉搜索树一样,小的在左边,大的在右边,只是当平衡因子绝对值大于1的时候需要对树进行旋转。
bool Insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.second)
{
//当前值小于要插入的值,往右边走
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.second)
{
//当前值大于要插入的值,往左边走
parent = cur;
cur = cur->_left;
}
else
{
//有相同的值了,退出插入
return false;
}
}
//当cur走到了nullptr,就是找到了要插入的点了
cur = new Node(kv);
//判断插入在左边还是右边
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;//确定父子关系
}
插入后更新平衡因子
平衡因子,如果在左边插入节点,那么它的父节点的平衡因子要-1,反之+1
case1:
parent节点的平衡因子为0,说明整棵树的高度并没有发生改变,只是补齐了原本缺节点的位置,所以遇到parent->_bf=0的时候,就不需要在修改平衡因子了
case2:
parent节点的平衡因子的绝对值为-1,就说明往上走可能存在abs(parent->_bf)=2的,所以要往上一直找。
parent=parent->_parent;
cur=cur->_parent;如果
abs(parent->_bf)=2就需要对其进行旋转来调整树的结构了。
while (parent)
{
//更新平衡因子
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 0)
{
//没有新增高度
break;
}
else if(abs(parent->_bf)==1)
{
//平衡因子为1,往上面继续找
parent = parent->_parent;
cur = cur->_parent;
}
else if (abs(parent->_bf) == 2)
{
//需要旋转了
}
}
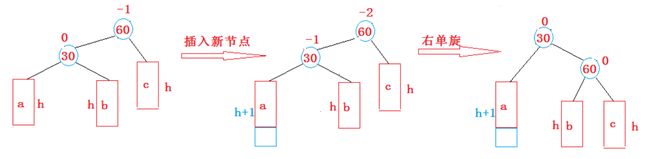
AVL树的右单旋
新节点插入较高左子树的左侧—左左:右单旋
例如上面的抽象图,当平衡树失衡的时候就需要调节平衡了,过程如上图所示。
具体图如下:
这里的操作就是将
subL作为一个根节点,将subLR作为parent的左节点(如果subLR存在的话),parent作为subL的右子节点。左旋的条件是
parent->_bf==-2&&cur->_bf==-1旋转之后
parent的平衡因子为0,subL的平衡因子也是0。
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
Node* pparent = parent->_parent;
//防止空指针
if (subLR)
{
subLR->_parent = parent;
}
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
//如果parent就是根节点
_root = subL;
subL->_parent = nullptr;
}
else
{
//如果parent只是一颗子树的根节点,就还需要连接好parent
//判断是左还是右节点
if (pparent->_left == parent)
{
pparent->_left = subL;
}
else
{
pparent->_right = subL;
}
subL->_parent = pparent;
}
subL->_bf = parent->_bf = 0;
}
AVL树的左单旋
新节点插入较高右子树的右侧—右右:左单旋
方法和右单旋类似。
当**
parent->_bf==2&&cur->_bf==1**的时候触发左单旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* pparent = parent->_parent;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = subR;
}
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = subR;
}
else
{
pparent->_right = subR;;
}
subR->_parent = pparent;
}
subR->_bf = parent->_bf = 0;
}
可以发现,如果满足左/右单旋的条件都是在同一条直线上,那如果路径不是在同一条直线上呢?
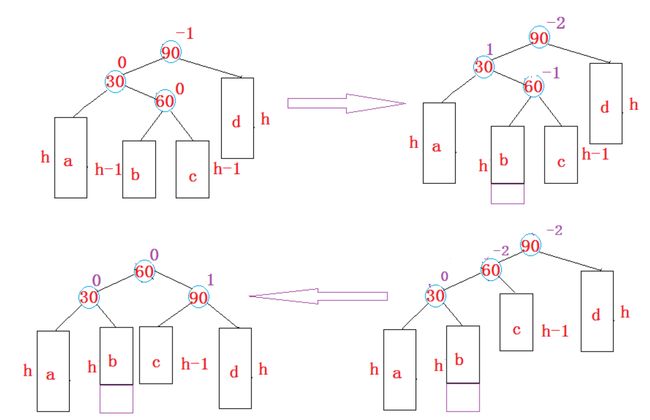
先左单旋再右单旋
新节点插入较高左子树的右侧—左右:先左单旋再右单旋
如果将节点插入到c当中,平衡因子就会发生改变,所以这里的平衡因子需要分情况讨论。
这里通过
subLR的平衡因子来确定是在左边插入还是在右边插入。两种情况下
subLR都是0。
下图是最简单的双旋:
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
subRL->_bf = 0;
if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
}
else
{
assert(false);
}
}
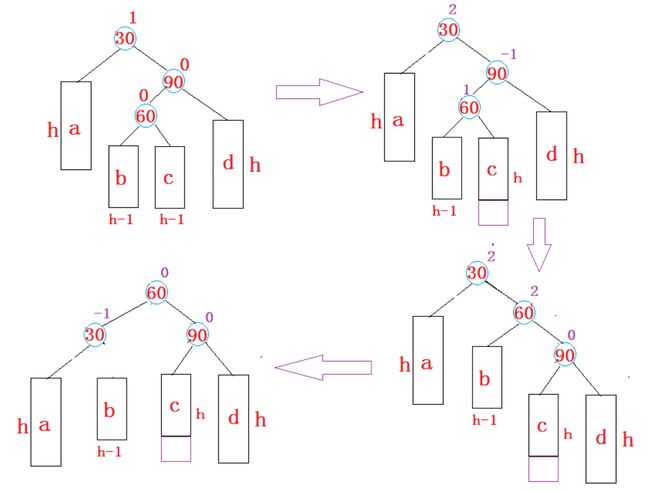
先右单旋再左单旋
新节点插入较高右子树的左侧—右左:先右单旋再左单旋
C增加节点之后高度和d一样都是h,将其全部旋转到右边去,然后再通过左旋把30压下去,将60作为根节点。
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL-> _right;
int bf = subLR->_bf;//提前存好,旋转后会subLR会发生改变
RotateL(parent->_left);
RotateR(parent);
subLR->_bf = 0;
if (bf == 1)
{
//在右边插入
parent->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
}
else if (bf == 0)
{
//已经平衡了
parent->_bf = 0;
subL->_bf = 0;
}
else
{
//插入存在问题
assert(false);
}
}
检查是否满足AVL树
通过计算左右子树的高度来确定是否满足AVL树,因为平衡因子是自己设置的,如果还通过平衡因子来确定的话会不太准。
bool _IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}
int leftHT = Height(root->_left);
int rightHT = Height(root->_right);
int diff = rightHT - leftHT;
if (diff != root->_bf)
{
cout << root->_kv.first << "平衡因子异常" << endl;
return false;
}
return abs(diff) < 2
&& _IsBalance(root->_left)//递归左子树
&& _IsBalance(root->_right);//递归右子树
}
int Height(Node* root)
{
if (root == nullptr)
return 0;
int left = Height(root->_left);
int right = Height(root->_right);
return max(left, right) + 1;
}
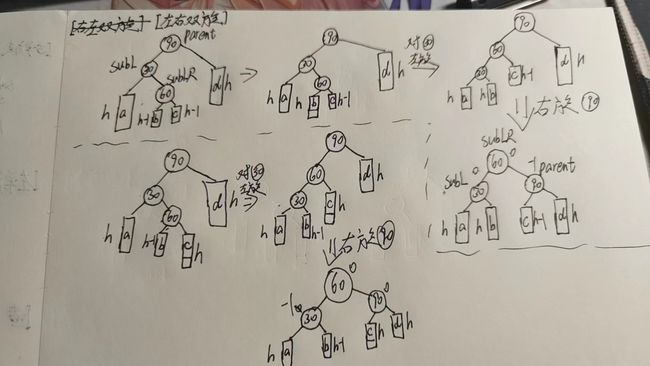
手写旋转过程:
总代码
#pragma once
#include
#include
using namespace std;
template
struct AVLTreeNode
{
AVLTreeNode* _left;
AVLTreeNode* _right;
AVLTreeNode* _parent;//父亲节点
pair _kv;// key / value
//构造函数
AVLTreeNode(const pair& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{}
int _bf;//平衡因子
};
template
class AVLTree
{
typedef AVLTreeNode Node;
public:
bool Insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.second)
{
//当前值小于要插入的值,往右边走
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.second)
{
//当前值大于要插入的值,往左边走
parent = cur;
cur = cur->_left;
}
else
{
//有相同的值了,退出插入
return false;
}
}
//当cur走到了nullptr,就是找到了要插入的点了
cur = new Node(kv);
//判断插入在左边还是右边
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;//确定父子关系
//控制平衡因子
while (parent)
{
if (cur == parent->_right)
{
parent->_bf++;
}
else
{
parent->_bf--;
}
if (parent->_bf == 0)
{
break;
}
else if (abs(parent->_bf) == 1)
{
parent = parent->_parent;
cur = cur->_parent;
}
else if (abs(parent->_bf) == 2)
{
// 说明parent所在子树已经不平衡了,需要旋转处理
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
else if ((parent->_bf == -2 && cur->_bf == -1))
{
RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
else
{
assert(false);
}
}
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalance()
{
return _IsBalance(_root);
}
private:
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
subRL->_bf = 0;
if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
}
else
{
assert(false);
}
}
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL-> _right;
int bf = subLR->_bf;//提前存好,旋转后会subLR会发生改变
RotateL(parent->_left);
RotateR(parent);
subLR->_bf = 0;
if (bf == 1)
{
//在右边插入
parent->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
}
else if (bf == 0)
{
//已经平衡了
parent->_bf = 0;
subL->_bf = 0;
}
else
{
//插入存在问题
assert(false);
}
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* pparent = parent->_parent;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = subR;
}
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = subR;
}
else
{
pparent->_right = subR;;
}
subR->_parent = pparent;
}
subR->_bf = parent->_bf = 0;
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
Node* pparent = parent->_parent;
//防止空指针
if (subLR)
{
subLR->_parent = parent;
}
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
//如果parent就是根节点
_root = subL;
subL->_parent = nullptr;
}
else
{
//如果parent只是一颗子树的根节点,就还需要连接好parent
//判断是左还是右节点
if (pparent->_left == parent)
{
pparent->_left = subL;
}
else
{
pparent->_right = subL;
}
subL->_parent = pparent;
}
subL->_bf = parent->_bf = 0;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
bool _IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}
int leftHT = Height(root->_left);
int rightHT = Height(root->_right);
int diff = rightHT - leftHT;
if (diff != root->_bf)
{
cout << root->_kv.first << "平衡因子异常" << endl;
return false;
}
return abs(diff) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
int Height(Node* root)
{
if (root == nullptr)
return 0;
int left = Height(root->_left);
int right = Height(root->_right);
return max(left, right) + 1;
}
private:
Node* _root=nullptr;
};
void TestAVLTree1()
{
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 }; // 测试双旋平衡因子调节
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
AVLTree t1;
for (auto e : a)
{
t1.Insert(make_pair(e, e));
}
t1.InOrder();
cout << "IsBalance:" << t1.IsBalance() << endl;
}
可以看到是满足AVL树的。