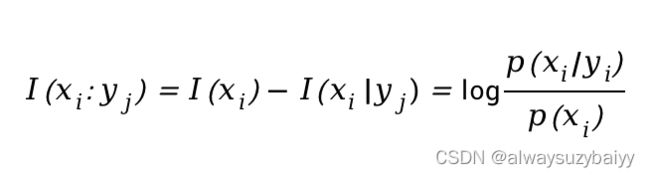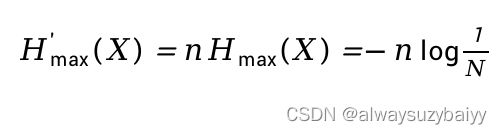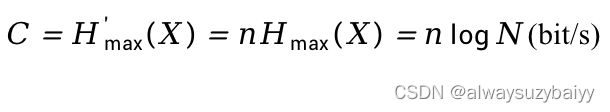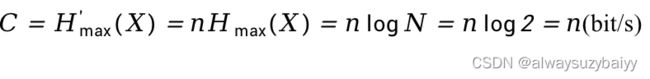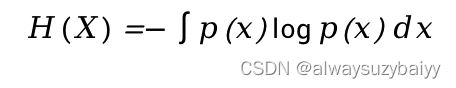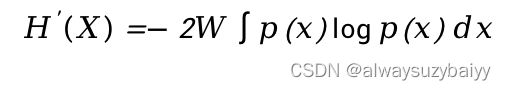信息与通信工程学科面试准备——信息论与编码｜保研推免面试题
目录
第一章 绪论
1 信息的概念
1.1 香农对信息的定义
1.2 信息与消息之间的关系？
2 信息的性质
3 信息的分类
4 信息论与编码研究的主要内容
(1)狭义信息论
(2)一般信息论
(3)广义信息论
5 信息论与编码的发展和应用
6 通信系统模型构成
(1)信源
(2)编码器
信源编码/器和信道编码/器的区别
通信系统的性质（有效性、可靠性）
(3)信道
(4)译码器
(5)信宿
第二章 基本信息论
1 信息量与自信息量、互信息量
(1)信息量定义
(2)自信息量
(3)互信息量
2 自信息量的单位与所用对数的底的关系
(1)以2为底
(2)以e为底
(3)以10为底
3 熵的定义
离散信源的熵
熵函数的性质
4 关于冗余度的定义
(1)相对熵
(2)冗余度
(3)信息变差
5 信道容量
离散信道的信道容量（离散无噪信道的信道容量）
6 共熵、条件熵与信源熵之间的关系
7 熵速率
连续信源的熵速率
8 平均互信息与信源熵，条件熵之间的关系
**选择题**
9 概率分布和不肯定程度间的关系
10 哈特莱对度量信源不肯定度公式
第二章练习题
一、填空题
二、选择题
三、计算题
第一章 绪论
本章首先引出信息的概念、性质以及信息的分类，然后介绍了信息论与编码研究的主要内容，最后简要介绍了信息论与编码的发展和应用。
1 信息的概念
1.1 香农对信息的定义
信息是对事物运动状态或存在方式的不确定性的描述。
1.2 信息与消息之间的关系？
消息与信息之间是包含和被包含的关系，消息包含着信息。消息之所以会含有信息是因为它的不确定性，一个不具有不确定性的消息不含有任何的信息。
2 信息的性质
(1)信息具有可度量性。虽然信息很抽象，但现在已有合理的度量方法。
(2)信息具有普遍性。信息在宇宙中普遍存在。
(3)信息具有可创造性。与能量的不能创造相比较，信息可以创造。
(4)信息具有无限性。在整个宇宙空间中，信息是无限的，即使在有限的空间中信息也是无限的。
(5)信息具有可传递性。信息可以从一方（信源）传送到另一方（信宿），也可以从一方传到多方。
(6)信息具有相对性。对于同一个事物，不同的观察者所获得的信息量可能不同。
(7)信息具有可加工性。信息可以被压缩（信源编码），被赋予抗干扰能力（信道编码）， 还可以被加密，而信息的内容不发生变化。
(8)信息具有转化性。从潜在的意义上讲，信息是可以转化的，它在一定条件下可以 转化为物质、能量和时间等。
(9)信息具有有序性。信息可用来消除系统的不定性，增加系统的有序性。
(10)信息具有共享性。同一信息可以被无限的人所获得，信息是可以共享的交流不会使交流者失去原有的信息，而且可以获得新的消息。
3 信息的分类
(1)按层次分类：信息可以分为语法信息、语义信息和语用信息。
(2)按信息的地位分类：信息可以分为客观信息和主观信息。
(3)按信息的作用分类：信息可以分为有用信息、无用信息和干扰信息。
(4)按信息的传递方向分类：信息可以分为前馈信息和后馈信息。
(5)按信息的逻辑意义分类：信息可以分为真实信息、虚假信息和不定信息。
(6)按信息的来源分类：信息可以分成语音信息、图像信息、文字信息、数据信息和计算信息等。
(8)按信息的应用部门分类：信息可以分成工业信息、农业信息、军事信息、政治信息、科技信息、文化信息、经验信息和市场信息等。
(9)按携带信息的信号性质分类：信息可以分成连续信息、离散信息和半连续信息等。
4 信息论与编码研究的主要内容
信息论研究的3个方面分别是：狭义信息论、一般信息论、广义信息论。
(1)狭义信息论
狭义信息论。又称为经典信息论，主要研究信息的度量、信道容量以及信源编码和信道编码等问题。这部分内容的理论基础是香农信息论，也称基本信息论。
(2)一般信息论
一般信息论。又称为工程信息论，主要研究信息的传输和处理问题。在一般论中也研究通信的基本理论，包括信号均噪声理论、信号过滤与检测、调制制度，编码等问题，所以，一般信息论也可以称为通信理论。
(3)广义信息论
广义信息论是一门综合、交叉的新兴学科，不仅包含上述两个方面的内容，而且包含所有与信息有关的自然科学和社会科学领域，如模式识别、计算机翻译、心理学、遗传学、生物学、经济学等，它也是新发展起来的光学信息论、量子信息论和生物信息论等的信息科学理论。
5 信息论与编码的发展和应用
6 通信系统模型构成
(1)信源
信源是产生消息和消息序列的源，它可以是人、生物、机器或其他的事物。信源是事物各种运动状态或存在的集合，例如，“各种气象状态”、“人的大脑思维活动”等。 信源的输出是消息，消息是具体的；但信源输出的消息是随机的、不确定的，有一定的规律性，因此，可以用随机变量或随机矢量等数学模型来表示信源。
(2)编码器
编码器可以分为信源编码器和信道编码器：
编码器是把消息变换成信号（如电信号、光信号、声信号等）的措施，编码器输出的是适合信道传输的信号。
信源编码/器和信道编码/器的区别
编码器可以分为两种：信源编码器和信道编码器。
信源编码是对信源输出的消息进行适当的变换和处理，压缩信源的冗余度来提高信息传输的效率，这是为了提高通信系统的有效性，信源编码又可以分为无失真信源编码和限失真信源编码。
信道编码是为了提高信息传输的可靠性而有目的地对信源编码器输出的代码组添加一些监督码元，使其具有纠错和检错的能力。
通信系统的性质（有效性、可靠性）
例如，老师讲课时需要把知识进行加工和提炼，以提高信息传输的有效性。为了让学生听得明白，有时又需要适当地重复，只是为了提高信息传输的可靠性。
在实际的通信系统中，可靠性和有效性常常是相互矛盾的，提高有效性必须去掉信源符号的冗余部分，但是这会导致可靠性的下降。而提高可靠性就需要增加监督码元，这又降低了有效性。有时为了兼顾有效性，就不一定要求绝对准确地在接收端再现原来的消息，而是可以允许一定的误差或失真，也就是说允许近似地再现原来的信息。
(3)信道
信道是指通信系统把载荷消息的信号从发送端送到接收端的媒介或通道。在狭义的通信系统中，实际的信道有明线、电缆、波导、光纤以及无线电波传播空间等，这些都属于电磁波能量的信道，对于广义的通信系统来说，信道还可以是其他的传输媒介。
信道除了传送信号外，还有存储信号的作用，如磁带、光盘或书写通信方式等。信息的传输不可避免地会引入噪声和干扰，为了分析方便，把系统所有其他部分的干扰和噪声都等效地折合成信道干扰，看成是一个噪声源产生的，并叠加于所传输的信号上，这样，信道输出的是已经叠加了干扰的信号。
(4)译码器
译码是编码的反变换，它是把信道输出的已编码的信号变成信宿能够理解的消息。译码器一般也可以分为信源译码器和信道译码器，它需要尽可能准确地再现信源输出的消息。在保密通信系统中，还应包括解密译码。
(5)信宿
信宿是消息传递的对象，即接收消息的人、机器或其他事物，信源和信宿可以处于不同的地点和不同的时刻。
第二章 基本信息论
本章介绍了信息量的概念，信息量包括自信息量和互信息量。熵是信息论中非常重要的概念，它分为信源熵、共熵和条件熵，熟悉它们之问的关系以及性质是非常必要的，同时又介绍了离散信源的冗余度。信道是信息传输的重要组成部分，它分为有噪信道、无噪信道、离散信道和连续信道，本章介绍了离散和连续无噪信道的熵速率和信道容量，同时又介绍了离散有噪信道的疑义度、散布度、接收熵速率和信道容量以及连续有噪信道的接收熵速率和信道容量，在这里得出了香农公式。
1 信息量与自信息量、互信息量
(1)信息量定义
信息量(I)=不肯定程度的减小量
也就是说，收信者收到一个消息后，所获得的信息量等于收到消息前后不肯定程度的减小量。
(2)自信息量
自信息量是一个事件(消息)本身所包含的信息量，它是由事件的不肯定程度决定的。不肯定程度与事件发生的概率有关，概率越小，不肯定度越大，那么它获得的信息量也就越大，所以，如果发生事件
的概率为
，它的自信息量司以定义为
(3)互信息量
用的后验概率与先验概率的比值来表示
关于的信息量，也就是互信息量，用表示
表示，公式为：
互信息量实际上就是已知事件后，所消除的关于事件的不肯定性，它等于事件本身的不肯定性
减去已知事件
后对仍然存在的不肯定性
。
2 自信息量的单位与所用对数的底的关系
(1)以2为底
通常取对数的底为2，信息量的单位为比特(bit，binary unit)。比特是信息论中最常用的信息量的单位，当取对数的底为2时，2常常省略，即用
表示
。
注意：计算机术语中bit是位的单位(bit, binary digit)，与信息量的单位不同。
(2)以e为底
若取自然对数（以e为底），自信息量的单位为奈特(nat，natural unit)。理论推导或用于连续信源时用以e为底的对数比较方便。
(3)以10为底
工程上用以10为底较方便。若以10为对数底，则信息量的单位为哈特莱帜(Hartley)。这是用来纪念哈特莱首先提出用对数来度量信息的。
3 熵的定义
信源具有不肯定性，所以把信源用随机变量X来表示。这样随机变量X的每一个可能取值的自信息量的统计平均值为随机变量X的平均自信息量，也就是随机变量自信息量的数学期望为平均自信息量，用H(X)来表示，表达式为
![H(X)=E[I(x_{i})]=-\sum_{i=1}^{N}p(x_{i})logp(x_{i})](http://img.e-com-net.com/image/info8/f95d19db5d744fff9bad675e33fbb1de.png){kind=small}
中的N为X的所有可能取值的个数。
离散信源的熵
实际上，平均自信息量又称为信息熵或信源熵，简称为熵，所以熵也用H(X)来表示。离散信源熵的表达式与平均自信息量是相同的，即离散信源熵H(X)的表达式为：
若概率空间的状态数为N，等概时的概率为P=1/N，这是的离散信源熵为
熵的单位由自信息量的单位决定，即取决于对数选取的底数，一般选取用以2为底的。一般情况下，信源熵并不等于收信者平均获得的信息量，只有在无噪的情况下，收信者才能正确无误地接收到信源所发出的消息，全部消除了H(X)大小的平均不肯定性，所以获得的平均自信息量就等于H(X)。而一般情况下，因为干扰和噪声的存在，收信者不能全部消除信源的平均不肯定性，获得的信息量将小于信源熵。
熵函数的性质
(1)熵函数H(X)具有非负性；
(2)熵函数H(X)是P(X)的连续函数；
(3)状态数为N，等概时，熵函数H(X)为N的单调增函数。
4 关于冗余度的定义
(1)相对熵
信源的实际熵H(X)与其最大可能熵Hmax(X)的比值定义为相对熵，用
表示：
(2)冗余度
定义(1)与相对熵的差为冗余度，用E表示：
(3)信息变差
信息变差又称为内熵，信源最大可能熵与实际熵之差定义为信息变差，用
表示：
相对熵，冗余度和信息变差都可以表示信源的冗余度情况。
5 信道容量
信道容量就是指信道对信源的一切可能的概率分布而言能够传送的最大熵速率，用C表示，其单位为bit/s。
离散信道的信道容量（离散无噪信道的信道容量）
在离散信道中，消息来源于离散信源，离散信源如果有N符号，符号间无相关性且等概分布时，则其输出熵最大，表达式为：
如果离散信道每秒最多传送n个信源符号，则最大熵速率为：
由信道容量的定义就可以得出信道容量C为：
那么当N=2，即只有两个符号（如“0”和“1”）的二元离散信源时，则信道容量为
这说明，二元信道的信道容量就等于每秒传送的符号数n。
6 共熵、条件熵与信源熵之间的关系
**选择题**H(X)，H(Y)为信源熵，H(Y|X)为条件熵，所以共熵、条件熵与信源熵之间的关系为:
H(XY)=H(X)+H(Y|X)
H(XY)=H(Y)+H(Y|X)
7 熵速率
信源在单位时间内输出的熵称为信源的熵速率，又称信息速率或传信率，用表示。根据信源的分类，熵速率也可以分为离散信源的熵速率和连续信源的熵速率。
连续信源的熵速率
连续信源的熵就是连续信源平均每个样值的熵，它完全由信源概率分布密度
来描述。由前面的分析可知连续信源的熵可表示：
**选择题**如果信源输出信号的带宽有限，最大为W，则根据采样定理，为了采样后不丢失任何信息，其采样率至少应为2W/s，因此连续信源的熵速率H‘(X)为
**选择题**如果信道每秒传输的消息数为n/s，则收信者接收到的熵速率R为
8 平均互信息与信源熵，条件熵之间的关系
**选择题**
I(X;Y)=H(X)-H(X|Y)
I(X;Y)=H(Y)-H(Y|X)
I(X;Y)=H(X)+H(Y)-H(XY)
9 概率分布和不肯定程度间的关系
信源概率空间的概率分布与不肯定程度之间的关系：一个信源可以用概率空间描述，它的不肯定程度可以用这个概率空间的可能状态及概率来描述。事件发生的概率越大，不肯定性就越小；而事件发生的概率越小，不肯定性就越大；对于发生概率等于1的必然事件，则不存在不肯定性。
10 哈特莱对度量信源不肯定度公式
哈莱特(R. V. L. Hartley)首先定义了度量信源不肯定度的公式，他指出：应该用信源概率空间的概率的倒数的对数来度量不肯定程度，也就是不肯定度与概率的倒数的对数成比例，即
通常令K=1，则
第二章练习题
一、填空题
1. 某事件x发生的概率为p(x)＝l，则此事件 不存在 （存在或不存在）不肯定性。
2. 信息量的单位与所用对数的底有关，当取以2为底时，单位为 bit ；取自然对数e时，单位为 nat ；取以10为底时，单位为Hartley。
3. 一离散信源输出二进制符号，在 信源等概率分布的 条件下，每个二进制符号携带1bit信息量，在 不等概率分布的 条件下，每个二进制符号携带额信息量小于1bit。
4. 二元信源由0和1两个符号构成，信源符号等概率分布，且符号之间无相关性，如果发送12个符号，这12个符号所含朗信息量为12bit 。
5. 离散二元符号序列中的各个符号概率为
，则自信息量
。
6. 一输出为A、B、C和D的四个符号的信源，等概输出时，信源熵为 2bit 。
7. 若信源熵为
，信源熵的最大值为
，那么冗余度E可表示为，内熵可表示为
。
8. 以二元离散信源为例，它由0和1两个符号构成，此信源传输时经过离散信道，信道每秒最多传送5个信源符号，则信道容量为5bit 。
二、选择题
见标记**选择题**