Android OpenGL ES2.0从放弃到入门(四)—— 绘制圆柱体和球体
上一篇文章,我们绘制了部分几何图形和立方体,今天我们来绘制点带弧面的立体图形
圆柱体
圆柱体咋一看有点费劲,我们不妨拆解来看。一个圆柱体可以分为两个圆形底面和一个弧面的侧面。在前面我们已经画过圆形了,我们这里就考虑弧面去如何实现就行了。类比圆形的实现原理,我们也可以把侧面圆筒一样的弧面,分解成棱柱,分解的越细、棱柱的面越多看起来就和圆筒是一样的了。而每个棱柱的面都是个矩形,我们再把矩形拆解成两个三角形,这样就可以了。来看看代码怎么实现的。
ArrayList<Float> pos = new ArrayList<>();
float angDegSpan = 360f / n;
for (float i = 0; i < 360 + angDegSpan; i += angDegSpan) {
pos.add((float) (radius * Math.sin(i * Math.PI / 180f)));
pos.add((float) (radius * Math.cos(i * Math.PI / 180f)));
pos.add(height);
pos.add((float) (radius * Math.sin(i * Math.PI / 180f)));
pos.add((float) (radius * Math.cos(i * Math.PI / 180f)));
pos.add(0.0f);
}
float[] d = new float[pos.size()];
for (int i = 0; i < d.length; i++) {
d[i] = pos.get(i);
}
上面我们就得到圆筒侧面的相关坐标了,还剩上下两个底面,之前我们在写圆的时候,把Z数值写成了height,这里就派上用场了。
private Circle ovalBottom, ovalTop;
...
ovalBottom = new Circle();
ovalTop = new Circle(height);
为了能让圆柱看起来更立体点,我们让底部圆筒的部分颜色稍微改一改,这部分在顶点着色器中实现
uniform mat4 vMatrix;
varying vec4 vColor;
attribute vec4 vPosition;
void main(){
gl_Position=vMatrix*vPosition;
if(vPosition.z!=0.0){
vColor=vec4(0.0,0.0,0.0,1.0);
}else{
vColor=vec4(0.9,0.9,0.9,1.0);
}
}
可以看到,当z==0的时候,设置了一个接近于黑色的颜色。来看一下效果

球体
如果说圆柱还能拆解拆解,这个可咋整,关于球体也可以拆分,下面来介绍下球体的拆分的两种方法——正多面体法和经纬度法
-
正多面体法:
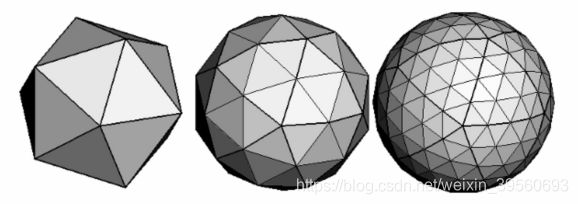
这种思想还是和画圆类似,如果多面体足够的多,那看起来不就是球了吗。看似很容易理解,但是转换成代码可就犯难了,XYZ坐标可怎么计算?学渣的我表示这个真够呛。 -
经纬度法:把点拆解成经纬度坐标,再连接成各个面,最后去拼成一个球。

我们生活的地球就是一个球体,在地球上去定位一个地点用的就是经纬度,这种方法去计算点坐标就容易多了,最起码有法可循。
球面点坐标
可就算是球面坐标怎么计算我也不清楚,这时候问了问度娘球坐标系。我们先来了解下球的坐标系:

在数学里,球坐标系(英语:Spherical coordinate system)是一种利用球坐标 表示一个点 p 在三维空间的位置的三维正交坐标系。原点到 P 点的距离 r ,原点到点 P 的连线与正z轴之间的天顶角θ 以及原点到点 P 的连线,在 xy平面的投影线,与正 x轴之间的方位角φ 。
需要注意的是,球坐标系与我们OpenGL的坐标系是不一样的,在写代码的时候需要注意。知道了坐标系,来看一下点坐标如何去计算:
x=Rsinθcosφ
y=Rsinθsinφ
z=Rcosθ
理解了以上基本知识,我们通过代码来创建我的球面坐标:
private float[] createBallPos() {
//球以(0,0,0)为中心,以R为半径,则球上任意一点的坐标为
// 其中,a为圆心到点的线段与xz平面的夹角,b为圆心到点的线段在xz平面的投影与z轴的夹角
ArrayList<Float> data = new ArrayList<>();
float r1, r2;
float h1, h2;
float sin, cos;
// 遍历纬度
for (float i = -90; i < 90 + step; i += step) {
//Math.sin(x) x 的正玄值。返回值在 -1.0 到 1.0 之间;X 都是指的“弧度”而非“角度”,弧度的计算公式为: 2*PI/360*角度
//计算当前点与圆心连线,与Y轴夹角θ的正余弦值(此坐标系为openGL坐标系)
/**
* 以下坐标系为openGl坐标系
* 此处计算当前纬度与Z轴夹角的正余弦值,由于根据公式,应该计算与Y轴的正余弦,但因为互余夹角sin与cos相等,所以按此计算没有问题
* 后续的X的坐标就变成了x=R*cos*cos,所有关于θ的角的sin值都变换为cos计算
*/
r1 = (float) Math.cos(i * Math.PI / 180.0);
r2 = (float) Math.cos((i + step) * Math.PI / 180.0);
h1 = (float) Math.sin(i * Math.PI / 180.0);
h2 = (float) Math.sin((i + step) * Math.PI / 180.0);
// 固定纬度, 360 度旋转遍历一条纬线
float step2 = step * 2;
for (float j = 0.0f; j < 360.0f + step; j += step2) {
// 计算当前点在XZ平面投影,与Z轴的夹角φ的正余弦值(此坐标系为openGL坐标系)
cos = (float) Math.cos(j * Math.PI / 180.0);
sin = (float) Math.sin(j * Math.PI / 180.0);
data.add(r2 * cos);
data.add(h2);
data.add(r2 * sin);
data.add(r1 * cos);
data.add(h1);
data.add(r1 * sin);
}
}
float[] f = new float[data.size()];
for (int i = 0; i < f.length; i++) {
f[i] = data.get(i);
}
return f;
}
眼尖的童鞋可能发现了,之前不是说 x=Rsinθcosφ吗,怎么转成代码变成 x=Rcosθcosφ了。这方面代码上有备注,在两个角互为余角的时候,sin与cos的数值是一样的。除了需要注意两种坐标系的不同外,上述循环的常量90和360,为角度。
同样为了让我们的球体看起来也能立体,我们也写个专属球体的顶点着色器:
uniform mat4 vMatrix;
varying vec4 vColor;
attribute vec4 vPosition;
void main(){
gl_Position=vMatrix*vPosition;
float color;
if(vPosition.z>0.0){
color=vPosition.z;
}else{
color=-vPosition.z;
}
vColor=vec4(color,color,color,1.0);
}
以上就是圆柱体和球体的绘制。这里要感谢下湖广午王的微博,本文的资料和思路,有很多都是来自大神的博客,再次表示感谢。
我们到现在为止,画的都是些规则的几何图形,但是现实中的物体肯定不能都是规则的,花草树木怎么去绘制,在下一篇微博,我们就要去绘制下现实中的物体——Android OpenGL ES2.0从放弃到入门(五)——绘制3D模型(obj+mtl)
源码地址
关于OpenGL代码全部在一个项目中,托管在Github上——OpenGL4Android
