拓扑排序

1.前言

​ 在正式讲拓扑排序之前，我们来引入一下，以便各位更好理解。

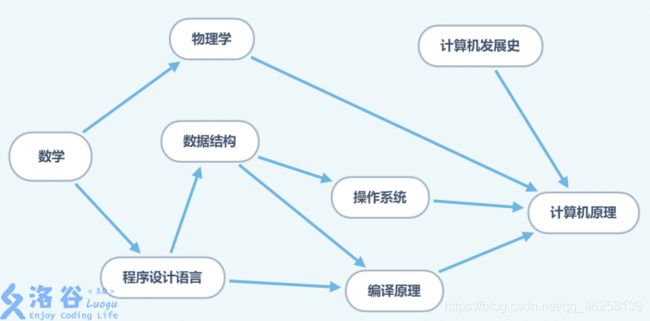
​ 首先，你想学习计算机的原理怎么办？（白手起家）肯定有很多前置知识啊！流程图就像下面：

​很明显，此时你需要按一定顺序（这个顺序叫 “拓扑序列”）学习才能彻底了解计算机原理。那么这个顺序怎么求呢？拓扑排序帮你忙！

​前置知识：图的基本概念以及建图编程能力

2.基本思路 & 实现

​首先，对于点的关系，大致分为 $2$ 种关系：

1. 先后关系，如上图的 “数学” 与 “物理学” 的关系。
2. 并列关系（应该叫做“没有关系”），如上图的 ”物理学“ 和 “计算机发展史” 的关系。

不难发现，因为有了并列关系，拓扑序列不一定是$唯一$的。

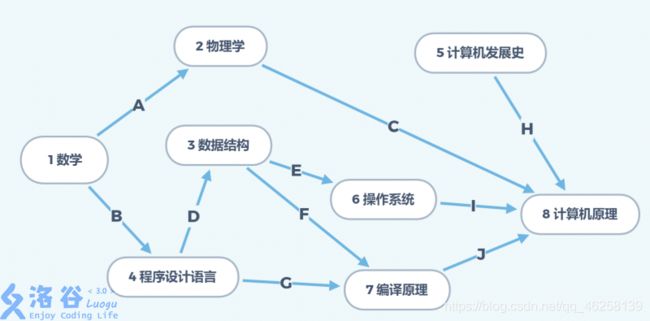
​ 如上图，可以得到很多个拓扑序列，这里只举一个例子，其他的相信大家都会看。

$\mathsf{上}\mathsf{图}\mathsf{的}\mathsf{一}\mathsf{个}\mathsf{拓}\mathsf{扑}\mathsf{序}\mathsf{列}：12345678$

​ 那么大家不难发现，拓扑排序的时候，大家总会找入度为 $0$ 的点，因为这是你不用学习的点，可以直接解锁。

​找到了之后， 你就可以把这个点放到序列里，从图中，删除该顶点，以及相关联的边，
那么随之就有新的点的入度为 $0$ ，然后重复上述直到图空。

​ 以上就是拓扑排序的基本思路！我们可以简述为：

1. 从图中，选择一个入度为 $0$ 的点，并输出该顶点；
2. 从图中，删除该顶点，以及相关联的边；
3. 重复上述步骤，直到输出所有点。

（原来如此简单！ ）

下面带大家模拟一遍拓扑排序的过程（大家觉得烦可以跳过）。

3. 模拟思路

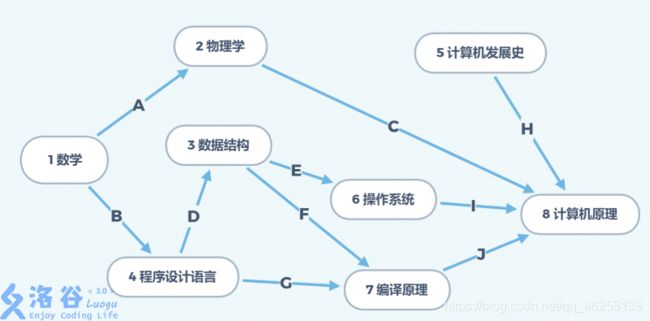
​ 首先，可以轻易发现，只有点 $1$ 是入度为 $0$，因此， 把它输出，删除点 $1$ 和边 $A$ 、 $B$ 。如下图：

​ 糟了，有 $4$个点的入度为 $0$ 怎么办？

​ 不着急，由于拓扑序列不止一个的原因，怎样都行，我就按照从小到大来。

​ 但是为了加快进度，我们直接删掉 $4$ 个点，并从小到大入拓扑序列，同时删除 $H$ 、 $C$ 、 $E$、 $F$ 、 $D$ 、 $G$ 六条边！

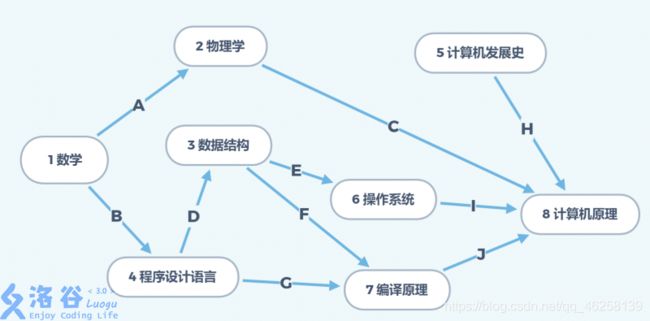
现在就很明了啦，把点 $6$ 、 $7$ 和相关的边删掉，入队，再把点 $8$ 删掉就完工！

最终拓扑序列：$12345678$

​ 关键来了，怎么用代码实现呢？（其实也不考码力(>_<)）

4. 代码实现

​ 拓扑排序一般有三种实现方法（建图是必不可少的）：

1. 算法设置一个队列（方便使用优先队列，字典序从小到大输出）,将所有入度为 $0$ 的顶点入队。找入度为 $0$ 的顶点,只要依次出队即可。删除边的操作转化为将该点关联的所有点的入度减 $1$ 。此算法有点像 $BFS$（我喜欢用这个）
2. 类似于 $DFS$ 用一个栈来存排序后的顺序，从一个顶点开始访问，依次访问它的邻接顶点，回溯的时候将当前结点压入栈。此时入度为 $0$ 的顶点（因为你已经访问过所有邻接顶点）一定是最后压入栈的。
3. 直接用 $DFS$ 搜索各个节点，码量小，时间复杂度只在常数上比上面慢。因此这里不再赘述这种方法。

现在很明显，由于要改变点的入度，因此我们需要一个数组保存入度（核心），并执行相应操作。

对于有向无环（DAG）图，输出拓扑序列（保证只有一种）的程序。程序如下（用邻接表和方法 $1$）：

#include
using namespace std;
const int maxn=1e5+99;

inline int read() 
{
	int x = 0, f = 1;
	char c = getchar();
	while(c > '9' || c < '0') {if(c == '-') f = -1;c = getchar();}
	while(c >= '0'&&c <= '9') {x = x * 10 + c - '0';c = getchar();}
	return x * f;
}

int n,m,t,tot,cnt;
int head[maxn],ind[maxn];
int ans[maxn];
//indeg[i]是第i个点的入度；ans[]是答案队列

struct Edge
{
	int to,next;
}e[maxn];

void add(int a,int b)
{
	e[++tot].to=b;
	e[tot].next=head[a];
	head[a]=tot;
}

void init()
{
	ans.clear();
	tot=0;
	cnt=0;
	memset(head,0,sizeof(head));
	memset(ind,0,sizeof(ind));
}

void topo()
{
	queue<int> q;
	for(int i=1;i<=n;i++)
		if(!ind[i])q.push(i);//将所有入度为0的点入队
	while(!q.empty())//开始搜索
	{
		int tmp=q.front();
		q.pop();
		ans[++cnt]=tmp;//入度为0的点记得放到答案队列里
		for(int i=head[tmp];i;i=e[i].next)//删边的操作转化为入度减1
		{
			if(--ind[e[i].to]==0)q.push(e[i].to);//如果这个点变成入度为0，入队列
		}
	}
}
int main()
{
	t=read();
	while(t--)
	{
		init();
		n=read();m=read();
		for(int i=1,a,b;i<=m;i++)
		{
			a=read();b=read();
			add(a,b);
			ind[b]++;//建图，同时统计入度
		}
		topo();
		for(int i=1;i<=cnt;i++)cout<<ans[i]<<" ";
	}
}

​ 此程序时间复杂度显而易见，邻接表时间复杂度 $O(n+e)$。

​ 用栈实现的拓扑排序也是一样的道理。

​ 看到这，应该会有人好奇，为什么不需要 $bool$ 的 $visit$ 数组来标记是否走过这点呢？（你以为是SPFA呢 ）

答案是：不用标记。因为：（转自@ $lyz0$ 讨论帖的一句话）

在某个结点被弹出队列时，队列中的结点一定不是它的前驱结点，那个结点就一定不会再次入队。

​

因此，既然节点不会二次入队，所以就不需要 $visit$ 数组~！同时，也因为拓扑排序保证每个节点、每条边只被访问过一次，因此时间复杂度是线性的，为 $O(n+e)$，而不是 $O(ne)$（前提是你用的邻接表）。

毕竟一般情况下，邻接表还是比邻接矩阵高效。

但是你以为放出了程序就结束了吗？当然不是！！！继续观察下面这幅图：

​ 你可以很明显的发现，拓扑排序的对象只能是个有向无环图（简称DAG）！如果有闭环，那么你将没有入度为 $0$ 的点产生，拓扑排序就异常终止……同时，只要这是个有向无环图，那么它至少有一个拓扑序列。

​ 所以，判断这个图是否有闭环就显得很重要！该如何判断呢……（会的可以跳过）

第一种最简单的方法：用拓扑本身

​ 前面说到拓扑排序保证每个节点、每条边只被访问过一次，因此我们只要看一下答案数组存储个数有没有节点数那么多，就可以判断是否有环。有环的话，那么节点就无法入队列，答案数组就会缺。程序如下（代码只多了一个 $if$ 而已）：

#include
using namespace std;
const int maxn=1e5+99;

inline int read() 
{
	int x = 0, f = 1;
	char c = getchar();
	while(c > '9' || c < '0') {if(c == '-') f = -1;c = getchar();}
	while(c >= '0'&&c <= '9') {x = x * 10 + c - '0';c = getchar();}
	return x * f;
}

int n,m,t,tot,cnt;
int head[maxn],ind[maxn];
int ans[maxn];
//indeg[i]是第i个点的入度；ans[]是答案队列

struct Edge
{
	int to,next;
}e[maxn];

void add(int a,int b)
{
	e[++tot].to=b;
	e[tot].next=head[a];
	head[a]=tot;
}

void init()
{
	ans.clear();
	tot=0;
	cnt=0;
	memset(head,0,sizeof(head));
	memset(ind,0,sizeof(ind));
}

void topo()
{
	queue<int> q;
	for(int i=1;i<=n;i++)
		if(!ind[i])q.push(i);//将所有入度为0的点入队
	while(!q.empty())//开始搜索
	{
		int tmp=q.front();
		q.pop();
		ans[++cnt]=tmp;//判断环的核心，看答案数组是否有n个
		for(int i=head[tmp];i;i=e[i].next)
		{
			if(--ind[e[i].to]==0)q.push(e[i].to);
		}
	}
}
int main()
{
	t=read();
	while(t--)
	{
		init();
		n=read();m=read();
		for(int i=1,a,b;i<=m;i++)
		{
			a=read();b=read();
			add(a,b);
			ind[b]++;//建图，同时统计入度
		}
		topo();
		if(cnt<n)//判断是否有环，答案队列不足即有环
		{
			cout<<"NO";
		}
		for(int i=1;i<=cnt;i++)cout<<ans[i]<<" ";
	}
}

第二种，用 $DFS$

​ 用一个 $int$ 类型的 $visit$ 数组，标记节点，其中 $-1$表示回到自己，产生了环，直接 $return$ 。否则就继续 $DFS$ 跑一遍这个图，跑完了就没有环。时间复杂度 $O(n^2)$。个人建议还是用上面那种比较好，那么这个只是提一提，因为这个比较通俗易懂。

#include
#include
#include
using namespace std;

const int MAXN=10005;
int n,m;
bool a[MAXN][MAXN];//邻接矩阵建图
bool flag;//判断是否有环，有环就true
int visit[MAXN];//标记节点，注意是int类型，等会儿会说到

void input(void)
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int x,y;
        cin>>x>>y;
        a[x][y]=true;//建图
    }
} 

void dfs(const int& k)
{
    visit[k]=-1;//特殊标记
    for(int i=1;i<=n;i++)
    {
        if(visit[i]==0 && a[k][i]==true)//当前访问这个点并且有边
        {
            dfs(i);//继续访问
            visit[i]=1;//标记为1。注意：这里要放在dfs的后面，因为才不会被-1赋值的时候覆盖
        }   
        if(visit[i]==-1 && a[k][i]==true)//如果回到了自己本身（这就是-1的用处），证明有环
        {
            cout<<"有环！"<<endl;
            flag=true;//标记输出的
            return;//有环可以直接跳出
        }
    }   
   //重点还是要区分1和-1的赋值
}

int main()
{
    input();
    dfs(1);//从起点开始，视情况而变
    if(!flag)//flag的用处，标记输出
     cout<<"无环！"<<endl;
    return 0;
}

​ 其他判断闭环的方法，大家可以自行百度更优做法。（听说并查集可以）

5. 洛谷里的例题

​ 值得一提的是，拓扑排序通常都不单独出，而是配合其他算法综合考察。拓扑排序很多时候是个辅助 AKAK图论题的好帮手。给出下面几道例题大家刷刷吧。

• P4017 最大食物链计数：一道比较简单的题目，适合新手练。
• P1038 神经网络：拓扑排序比较经典题目（我们学校OJ也有）。
• P1983 车站分级： $NOIp$ 压轴题，拓扑排序+递推，值得一刷，练练思维。
• P1137 旅行计划：拓扑排序+ $DP$ 。这里只讲讲这道题目如何运用拓扑（可以进$blog$里看题解）。
• P3243 [HNOI2015菜肴制作]：正解恍然大悟，一点就通，值得一刷。

六、题解【P1137 旅行计划】

​ 这道题目大家一看就能发现，只能往东边走，并且有个入度为 $0$ 的起点，因此这是一个有向无环图，可以进行拓扑排序，求出拓扑序列。

​ 那么我们要拓扑序列怎么做呢？由于拓扑序列中，前面的点总是后面的点的前驱，因此可以进行 $dp$。

​ 而 $dp$ 式子也很明显，这个城市的路线只能由前面的城市过来（这也像拓扑），因此跟自己与前面城市路线 $+1max$ 一下，答案就出来了。

​ 当然，为了效率与内存，最好使用邻接表（建图就不说了）。

​ 具体看注释，参考程序如下：

#include
#include
#include
#include
using namespace std;

const int MAXN=100005;
int n,m,cnt;
int indeg[MAXN],f[MAXN],a[MAXN];
//三个数组分别表示：入度、dp数组、拓扑序列
struct node
{
    int to,next;
}edge[MAXN<<2];
int head[MAXN],sum;

void add(const int& x,const int& y)
{
    edge[++sum].next=head[x];
    edge[sum].to=y;
    head[x]=sum;
}

void input(void)
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
        indeg[y]++;//统计入度
    }
}

void topo_sort(void)//按上面教程说得来就行了
{
    queue <int> q;
    for(int i=1;i<=n;i++)
     if(!indeg[i])//初始化队列
      q.push(i);
    while(!q.empty())
    {
        const int tmp=q.front();
        q.pop();
        a[++cnt]=tmp;//把队列里的入度为0的点存进拓扑序列
        for(int i=head[tmp];i!=0;i=edge[i].next)//遍历一遍图
        {
            const int now=edge[i].to;
            indeg[now]--;
            if(!indeg[now])
             q.push(now);
        }
    }
}

void dp(void)
{
    for(int i=1;i<=n;i++)
     f[i]=1;//每个城市到本身都至少有1条路线
    for(int i=1;i<=n;i++)//每个城市都遍历一遍
    {
        const int tmp=a[i];//注意遍历的是拓扑序列里的城市，此时保证tmp是now的前驱
        for(int j=head[tmp];j!=0;j=edge[j].next)//遍历图
        {
            const int now=edge[j].to;
            f[now]=max(f[now],f[tmp]+1);//把有关联的城市都max一下
        }
    }   
}

void output(void)
{
    for(int i=1;i<=n;i++)
     printf("%d\n",f[i]);
}

int main()
{
    input();
    topo_sort();
    dp();
    output();
    return 0;
}