快速排序算法—图文详解，一篇就够了！

基本思想：

采用“分治”的思想，对于一组数据，选择一个基准元素（base），通常选择第一个或最后一个元素，通过第一轮扫描，比base小的元素都在base左边，比base大的元素都在base右边，再有同样的方法递归排序这两部分，直到序列中所有数据均有序为止。

图文详解 :

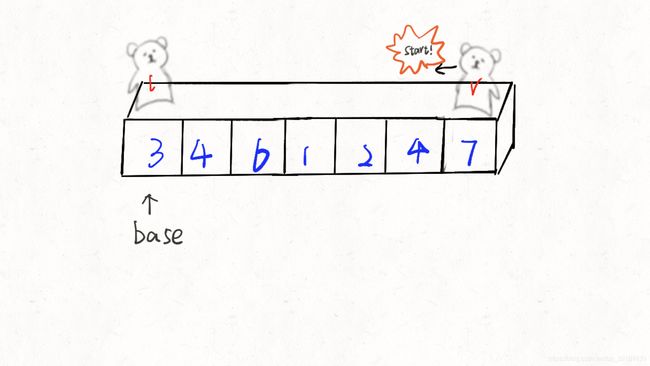
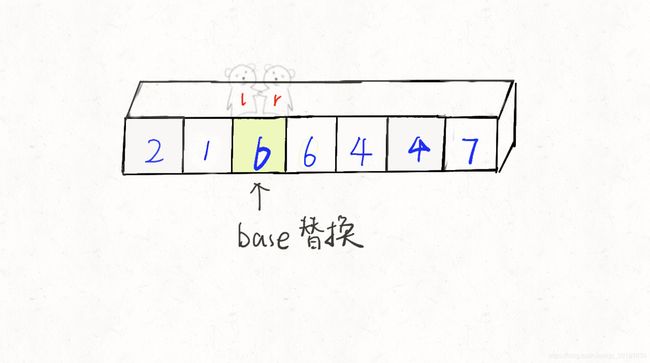
以 [3,4,6,1,2,4,7] 为例，以第一个元素3为base，定义左右两个指针（小熊l，小熊r），分别从两端开始扫描。从右向左找比3小的数，替换l所在位置的元素。再从左往右找比3大的数，然后替换r所在位置的元素。重复此过程直至两个小熊重合（两个指针指向同一元素），base替换此元素，此时第一轮结束。再递归排序base左右两部分的元素。

刚开始的时候让l 指向序列的最左边，指向数字3。让r 指向序列的最右边，指向数字 7。

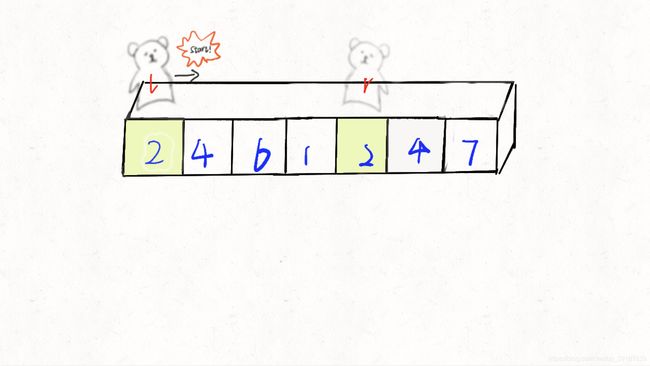
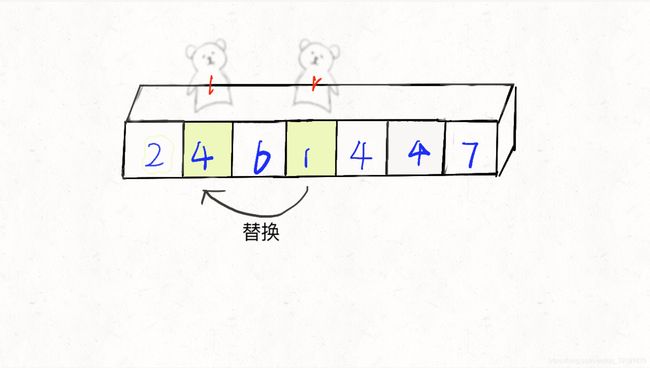
首先r出动，一步步向左移，直到找到比base小的数停下来，替换此时l所在位置的元素

替换后的序列为 [2,4,6,1,2,4,7]

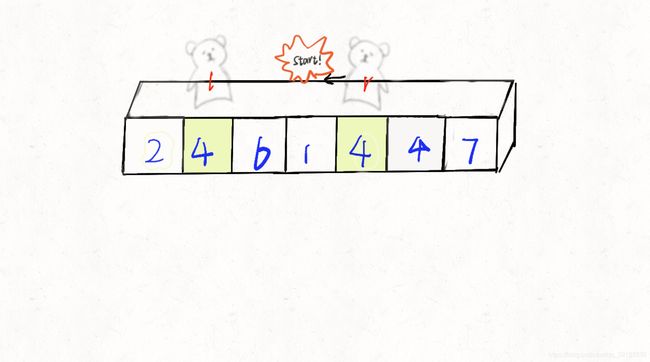
l出动，向右移直到找到比base大的数停下来，替换此时r所在位置的元素

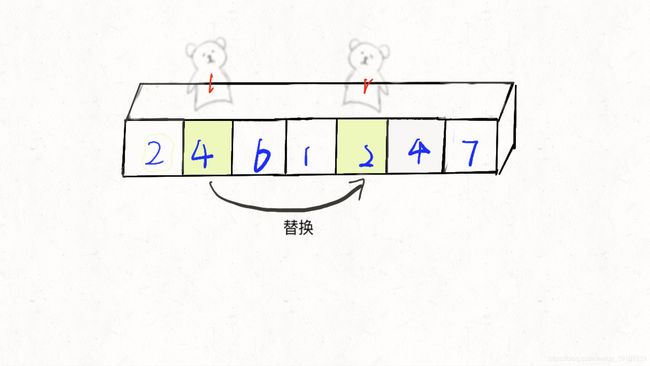
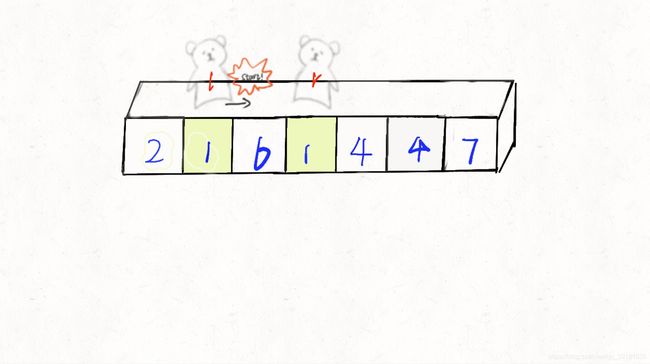
替换后的序列为 [2,4,6,1,4,4,7]，r再次出动，重复上述步骤

比base小，替换l所在位置的元素

替换后的序列为[2,1,6,1,4,4,7]，l再次出动

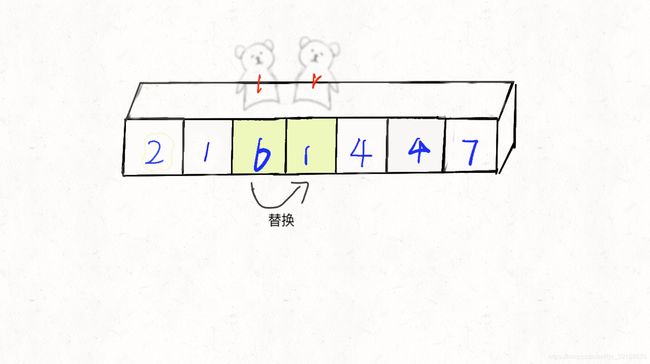
比base大，替换r所在位置的元素

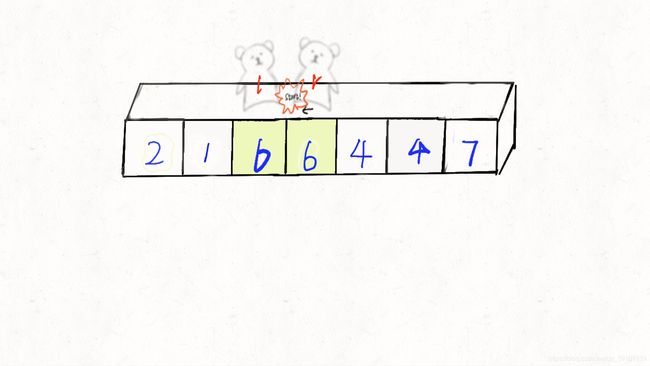
替换后的序列为[2,1,6,6,4,4,7]，r再次出动

此时l、r指向同一元素

base替换此元素

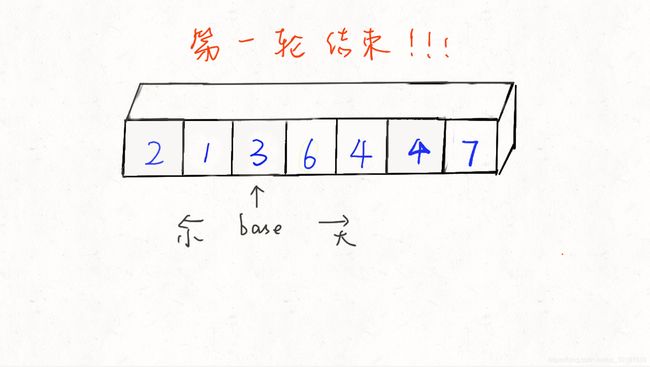
第一轮扫描完成，序列为 [2,1,3,6,4,4,7]，此时base(3)左边的元素都比它小，右边的元素都比它大，再对这两部分进行上述操作。

代码实现 :

public static void quickSort(int nums[], int start, int end) {
    //数组有多个元素进行排序
    if (start < end) {
        int base = nums[start];//以要进行排序数组第0个元素为base
        int left = start;//左指针
        int right = end;//右指针
        while (left < right) {
            //从右向左找，比base大，right--
            while (left< right && nums[right] >= base) {
                right--;
            }
            //比base小，替换left所在位置的数字
            nums[left] = nums[right];
            //从左向右找，比base小，left++
            while (left < right && nums[left] <= base){
                left++;
            }
            //比base大，替换right所在位置的数字
            nums[right] = nums[left];
        }
        nums[left] = base;//此时left=right，用base替换这个位置的数字
        //排列比base小的数字的数组
        quickSort(nums, start, left - 1);
        //排列比base大的数字的数组
        quickSort(nums, left + 1, end);
    }
}

采用分治的思想，先找到 每次分割的点 pos ，再排序。

/*
    left:数组左边界
    right：数组右边界
    */
    public void quickSort(int[] arr, int left, int right){
        if(left < right){
            int pos = partition(arr, left, right);
            helper(arr, left, pos - 1);
            helper(arr, pos + 1, right);
        }
    }
    public int partition(int[] arr, int left, int right){
        int base = arr[left];
        while(left < right){
            while(left < right && arr[right] >= base){
                right--;
            }
            arr[left] = arr[right];
            while(left < right && arr[left] <= base){
                left++;
            }
            arr[right] = arr[left];       
        }
        arr[left] = base;
        return left;
    }
}