LeetCode DAY41(198. House Robber&213. House Robber II&337. House Robber III)
Journey of LeetCode|DAY 41
- Preface
- 1. House Robber
-
- Analysis and Solution
-
- Dynamic Programming
- 2. House Robber II
-
- Analysis and Solution
-
- Dynamic Programming
- 3. House Robber III
-
- Analysis and Solution
-
- Dynamic Programming
Preface
This is a new day to continue my Dynamic Programming journey.
Learn something new and keep reviewing what I learnt before.
1. House Robber
LeetCode Link: 198. House Robber
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
Example 2:
Input: nums = [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.
Constraints:
1 <= nums.length <= 100
0 <= nums[i] <= 400
Analysis and Solution
Dynamic Programming
LeetCode C++ as followings Dynamic Programming
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.size() == 0) return 0;//remove case 0.0
if (nums.size() == 1) return nums[0];//remove case 0.1
vector<int> dp(nums.size());//build a vector
dp[0] = nums[0];//initialization
dp[1] = max(nums[0], nums[1]);//get the maxValue to attain the maxProfit
for (int i = 2; i < nums.size(); i++) {//traverse from front to end
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);//get the maxProfit
}
return dp[nums.size() - 1];
}
};
2. House Robber II
LeetCode Link: 213. House Robber II
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: nums = [2,3,2]
Output: 3
Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
Example 2:
Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
Example 3:
Input: nums = [1,2,3]
Output: 3
Constraints:
1 <= nums.length <= 100
0 <= nums[i] <= 1000
Analysis and Solution
Dynamic Programming
LeetCode C++ as followings Dynamic Programming
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.size() == 0) return 0;//remove case 0.0
if (nums.size() == 1) return nums[0];//remove case 0.1
int result1 = robRange(nums, 0, nums.size() - 2); // case 2: consider first element and without last element
int result2 = robRange(nums, 1, nums.size() - 1); // case3: consider last element without first element
return max(result1, result2);//get the maxValue to attain maxProfit
}
// main logic of rob
int robRange(vector<int>& nums, int start, int end) {
if (end == start) return nums[start];//remove the case 0.3 with only one element
vector<int> dp(nums.size());//build vector
dp[start] = nums[start];//initialization
dp[start + 1] = max(nums[start], nums[start + 1]);//initialization with maxValue
for (int i = start + 2; i <= end; i++) {//traverse from front to end
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);//get the maxProfit
}
return dp[end];
}
};
3. House Robber III
LeetCode Link: 337. House Robber III
The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.
Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.
Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police.
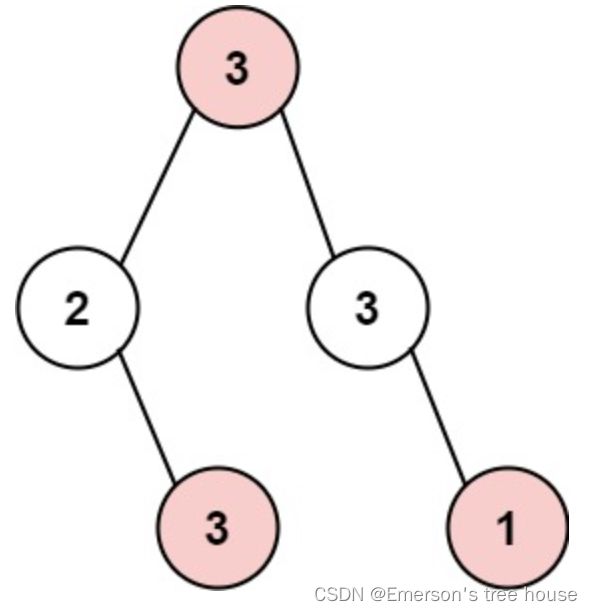
Input: root = [3,2,3,null,3,null,1]
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
Example 2:
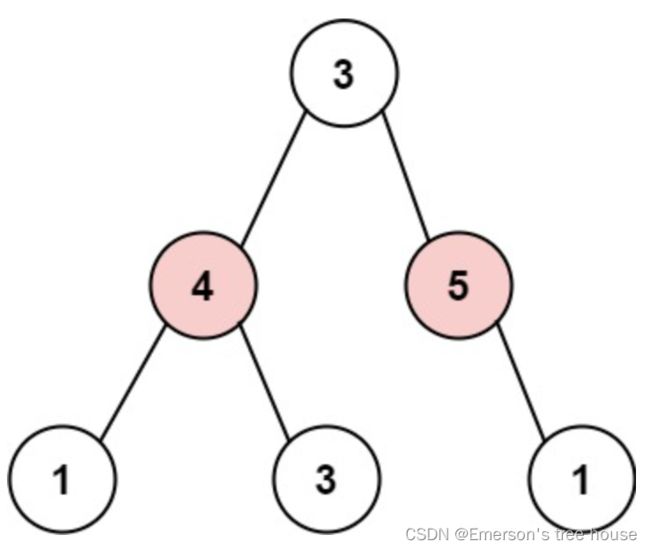
Input: root = [3,4,5,1,3,null,1]
Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.
Constraints:
The number of nodes in the tree is in the range [1, 10^4].
0 <= Node.val <= 10^4
Analysis and Solution
Dynamic Programming
LeetCode C++ as followings Dynamic Programming
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int rob(TreeNode* root) {
vector<int> result = robTree(root);//recursion
return max(result[0], result[1]);//result[0]:profit of no rob this node; result[1]: profit of robbing this node
}
vector<int> robTree(TreeNode* cur) {//build a array
if (cur == NULL) return vector<int>{0, 0};//remove case 0
vector<int> left = robTree(cur->left);//traverse left tree
vector<int> right = robTree(cur->right);//traverse right tree
// rob current node, stop robbing left and right node
int val1 = cur->val + left[0] + right[0];
// no rob current node, get the maxProfit to rob the left and right node
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};
}
};