论文阅读《2022WWW:Rethinking Graph Convolutional Networks in Knowledge Graph Completion》
论文链接
论文工作简介
KCN在建模图结构方面很有效。基于GCN的KGC模型通常使用编码器-解码器框架,GCNs和KGE模型分别充当编码器和解码器。
许多基于GCN的KGC模型虽然引入了额外的计算复杂度,但未能超越最先进的KGE模型?
作者发现GCNs中的图结构并没有对KGC的性能有显著提升,相反实体表示的转换为性能带来提升。本文提出的LTE-KGE模型带来与KGE模型相似的性能提升同时避免了GCN聚合中繁重计算负载。
尽管GCN引入了额外的计算复杂性,但基于GCN的模型并没有表现出比最先进的KGC模型更大的优势。(1)GCNs真的能带来性能增益吗?(2)在KGC中,GCNs的哪个因素至关重要?
GCNs真的能带来性能增益吗?
答案是肯定的。对于KGC任务, GCNs确实比KGE模型带来了性能增益。、
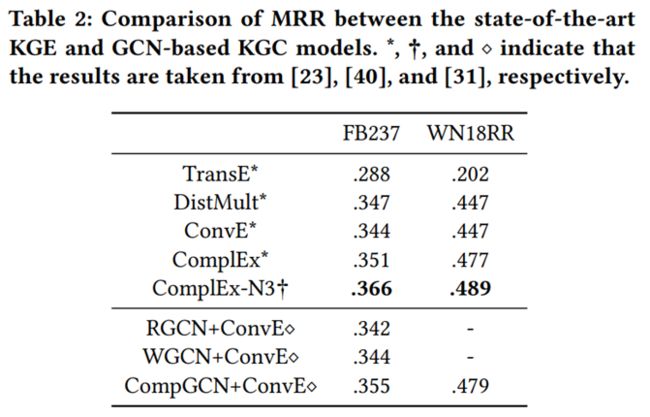
在大多数情况下,GCNs,尤其是最先进的CompGCN,显著提高了KGE模型的性能。在 FB237上,WGCN + TransE 在原始和复制情况下的表现都比 TransE差。在WN18RR上的 WGCN + DistMult/ConvE 也可以观察到类似的现象。这说明并不是所有的GCN都能提高所有KGE模型的性能。
GCNs的图结构建模在KGC中是否至关重要的探索较少,GCNs的哪个因素在KGC中至关重要尚不清楚。因此,本文进行了广泛的实验,以测试图结构、邻居信息、自环信息和关系的线性变换的影响。
GCNs的哪个因子在KGC中至关重要?-图结构
1 图结构
众所周知,GCNs在建模图结构方面是有效的。因此,如果我们打破图结构,基于GCN的KGC模型的性能预计将显著下降。
我们使用随机的邻接张量进行实验, 以探索图结构的影响。具体来说,在构建用于消息传递的邻接张量时,给定一个有效的三元组,我们将尾部实体替换为知识图谱中的一个随机实体。
注意,只在消息传递中使用随机邻接张量,而训练/验证/测试三元组保持不变。
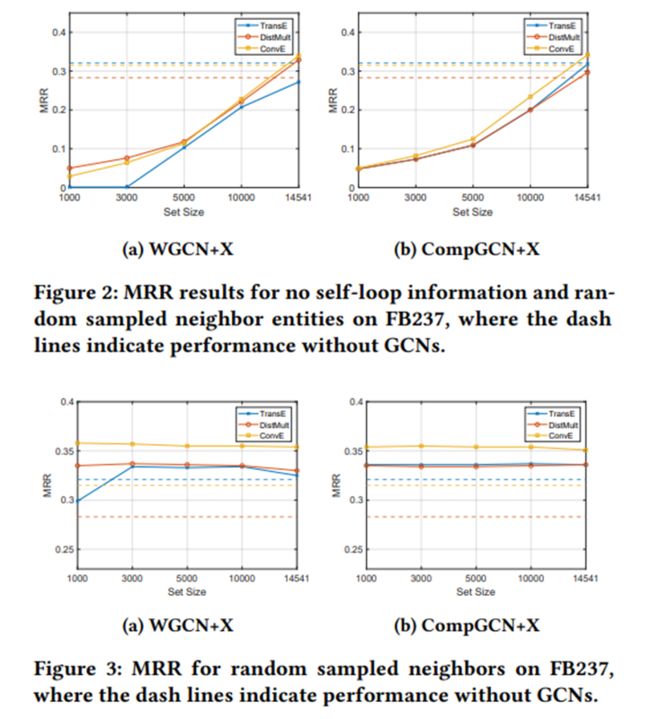
令人惊讶的是,随机破坏邻接张量,即图结构,并不影响基于GCN的KGC模型在两个数据集上的整体性能。具有随机邻接张量的模型获得了与其正常邻接张量对应的比较性能。对于WGCN+TransE,随机图结构甚至提高了FB237上 的性能。
结果表明,虽然GCN编码器可以提高KGE模型的性能,但GCNs中的图结构建模对性能提升并不至关重要。
GCNs的哪个因子在KGC中至关重要?-邻居信息
2 邻居信息
为了进一步探索GCNs中的图结构建模与性能提升之间的关系,我们进行了聚合过程中不使用邻居信息的实验。也就是说,GCNs中使用的图在节点(实体)之间没有边(关系),实体的新表示仅基于实体之前的表示生成。
表4显示,在两个数据集上,不使用邻居信息(X+WNI)的模型表现与原始模型相当。这表明,性能增益并非来自邻域聚合。
GCNs的哪个因子在KGC中至关重要?-自环信息
3 自环信息
为了确定性能增益是否需要自环信息,我们进行了无自环信息的实验。也就是说,一个实体的表征仅基于其邻域实体和关系的表征而生成。
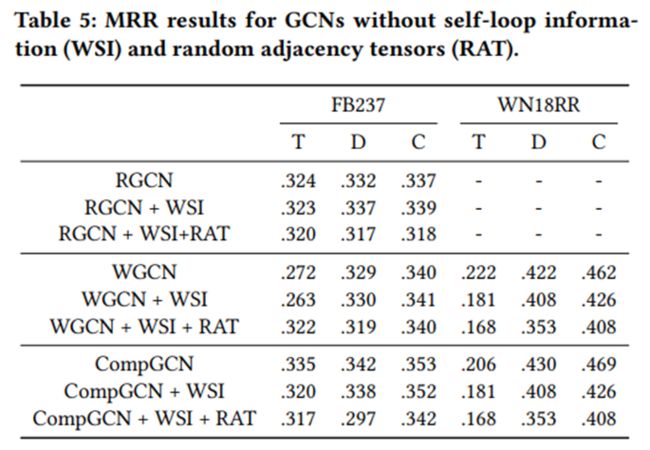
表5显示了不含自环信息(X+WSI)的结果。 令人惊讶的是,省略自环信息对大多数模型的性能也没有显著影响。
在大多数情况下,仅聚合邻居信息就可以实现与完全基于GCN的KGC模型的比较结果。进一步, 我们随机打破邻接张量,同时省略自环信息。由于这样只使用邻居信息,预计随机邻接张量会显著降低性能。
如图5 (X+WSI+RAT)所示,大多数解码器的性能只受到轻微影响。就是说,只聚合随机生成的邻居信息能实现与完全基于GCN的KGC模型的比较结果。
GCNs的哪个因子在KGC中至关重要?-思考
到目前为止,我们已经知道以下操作对基于GCN的KGC模型在FB237上的性能没有显著影响:
1)仅使用自环信息; 2)仅使用邻域信息; 3)只使用随机生成的邻居信息。
这三种情况有一个共同的性质:它们能够以高置信度区分具有不同语义的实体。
具体来说,如果我们只使用自环信息,每个实体的表示都是独立的,因此可以区分。
如果我们只使用邻居信息,两个实体只有拥有相似的邻居表示,才会具有相似的表示,这与KGC的假设是一致的:具有相似邻居的实体具有相似的语义。因此,我们可以区分具有不同语义的实体。
当从所有实体中随机抽样邻居实体时,我们以较高的可能性为不同的实体分配不同的邻居,从而我们可以通过聚合的实体表示来区分不同的实体。
GCNs的哪个因子在KGC中至关重要?-关系的线性变换
与RGCN和WGCN不同,CompGCN对关系嵌入应用线性变换。我们进行消融实验来探索变换的效果。
表6显示,除去关系的线性变换,除了在WN18RR上的CompGCN+TransE外,对性能没有显著影响。注意,TransE对超参数很敏感,我们并没有通过网格搜索找到最佳的超参数。CompGCN+TransE的性能可能会被低估。
因此,我们可以得出结论,关系的线性转换对于基于GCN的KGC模型并不重要。
基于GCN的KGC模型的嵌入更新过程有三个主要部分
1)基于图结构的聚合 2)实体转换 3)关系转换
我们已经展示了基于图结构的聚合和关系转换对基于GCN的KGC模型并不重要。因此,聚合实体表示的转换对性能改进至关重要。
一个简单而有效的框架 LTE-KGE
基于上面的观察,作者提出了一个简单但有效的KGC框架,即LTE-KGE,它使用线性转换的实体表示来实现与基于GCN的KGC模型的相似性能。
本文的目标不是提出一种新的最先进的KGC模型。而是想证明更简单的模型可以实现与最先进的基于GCN的模型相似的性能,现有复杂的GCN对于KGC来说可能是不必要的。
Wh和Wt是具有可训练权重的线性变换。
gh和gt,它们可以是来自函数集{identity函数,非线性激活函数,批量归一化,dropout}的函数组合。这些操作对应于基于GCN的模型中可能的非线性变换。
注意:
a)线性变换Wh和Wt可以根据实验结果共享相同的参数;
b) gh和gt根据实验结果可以是不同函数的组合;
c)由于每个实体都有自己的表示,LTE-KGE可以区分具有不同语义的实体;
d)当wh,wt 是单位矩阵,gh,gt是单位函数时,LTE-KGE模型恢复为KGE模型。
实验结果
作者对DistMult、TransE和ConvE进行了实验。具体来说,Wh和Wt是相同的,而gh和gt是DistMult/ConvE的批量归一化和dropout的组合,以及TransE的恒等函数。
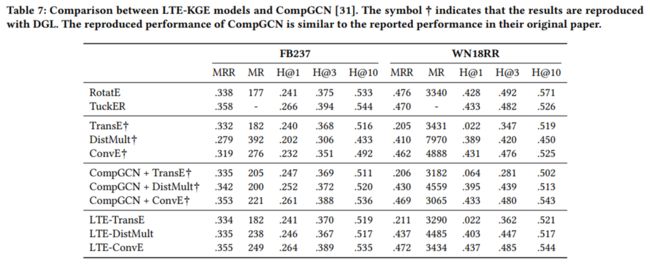
总体而言,LTE-KGE显著提升了 DistMult和ConvE的性能。
虽然LTE-KGE没有显式地对GCNs 这样的局部图结构进行建模,但它的性能与基于gcn的KGC 模型相当,有时甚至表现得更好。
作者还使用RotatE和 TuckER作为基线。结果表明,基于GCN的模型并没有始终表现出比这些KGE模型更大的优势。
如前所述,作者提出LTE-KGE来挑战GCN,不是实现最先进的性能。由于流行的基于GCN的模型不使用RotatE/TuckER作为解码器,因此我们也没有在它们之上构建LTE-KGE。