动态规划设计
文章目录
- 动态规划设计
- 一、什么是最长递增子序列?
-
- [300. 最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/)
- 注意子序列和子串的区别:
- 二、动态规划解法
-
- 2.1什么是数学归纳法?
- 2.2最长递增子序列中数学归纳的实际应用
-
- 如何找到动态规划的状态转移关系?
- 2.3 在leetCode上通过的代码
- 三、二分查找解法
-
- 怎么用到二分查找解法?
- 四、最长递增子序列的变种(拓展到二维)
-
- [354. 俄罗斯套娃信封问题](https://leetcode.cn/problems/russian-doll-envelopes/)
-
- 如何解决在二维数组上找最长递增子序列呢?
- 补充知识:Arrary.sort用 Comparator比较器定制排序方式
- 在leetCode上通过的代码:
动态规划设计
通过动态规划解题套路,我们知道了动态规划的套路:
- 找到了问题的状态
- 明确dp数组/函数的含义
- 定义了base case
但是在掌握了这些之后,我们仍然不知道如何确定选择也就是找不到状态转移的关系,依然写不出动态规划解法(动态规划的难点就在于寻找正确的状态转移方程)
针对这个问题,我们可以借助经典的最长递增子序列问题来学习设计动态规划的通用技巧:数学归纳思想
一、什么是最长递增子序列?
300. 最长递增子序列
最长递增子序列(Longest Increasing Subsequence,简写 LIS)是非常经典的一个算法问题
比较容易想到的是动态规划解法,时间复杂度为O(N^2)
比较难想到的是利用二分查找,时间复杂度是 O(NlogN)
比如说输入
nums=[10,9,2,5,3,7,101,18],其中最长的递增子序列是[2,3,7,101],所以算法的输出应该是 4。
注意子序列和子串的区别:
子串一定是连续的,而子序列不一定是连续的
二、动态规划解法
动态规划的核心设计思想是数学归纳法
2.1什么是数学归纳法?
比如我们想证明一个数学结论,纳闷我们就会先假设这个结论在k
如果能够证明出来 那么就说明这个结论对于k等于任何数都成立
类似的,我们设计动态规划算法,需要一个dp数组。
我们可以假设dp[0...i-1] 都已经被算出来了,然后问自己:怎么通过这些结果算出 dp[i]?
2.2最长递增子序列中数学归纳的实际应用
在此之前,我们首先要定义清楚dp数组的含义,即dp[i]的值到底代表什么?
dp[i]表示以nums[i]这个数结尾的最长递增子序列的长度。为什么这样定义?
这就是解决子序列问题的一个套路
其实在动态规划问题中,dp数组的定义方法也就几种
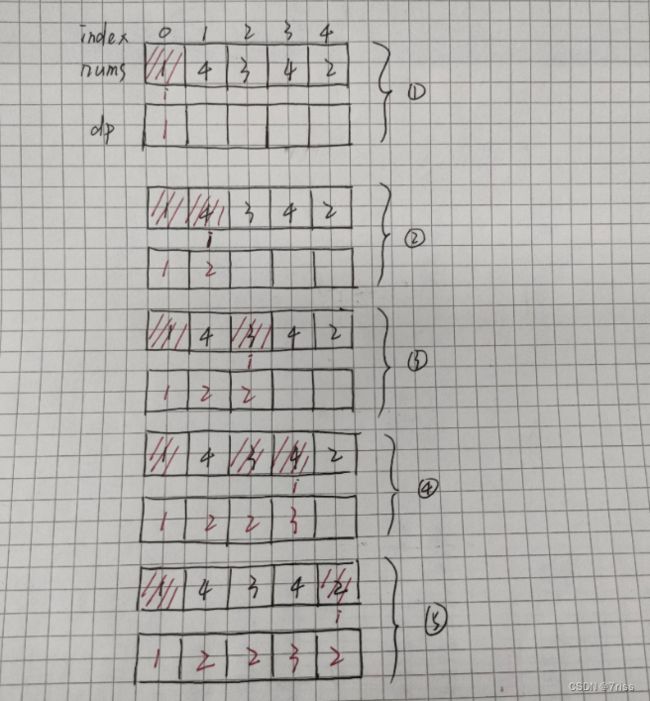
算法演进的过程:
-
根据这个定义,我们就可以推出base case
dp[i]初始值为1,因为以nums[i]结尾的最长递增子序列起码要包含它们自己
-
根据这个定义,我们的而最终结果(子序列的最大长度)应该是dp数组中的最大值
int res = 0; for (int i = 0; i < dp.length; i++) { res = Math.max(res, dp[i]); } return res; -
那现在我们要如何设计算法逻辑进行状态转移才能正确运行呢?也就是说我们如何使用数学归纳的思想
假设我们已经知道了dp[0…4]的所有结果,我们如何通过这些已知结果推出dp[5]呢?
根据刚才我们对dp数组的定义,现在想求dp[5]的值,也就是想求以nums[5]为结尾的最长递增子序列
nums[5]=3既然是递增子序列,
我们只要找到前面那些结尾比3小的子序列,
然后把3接到这些子序列末尾就可以形成一个新的递增子序列而且这个新的子序列长度加1
-
那现在nums[5]前面有哪些元素小于nums[5]?
我们可以用for循环比较一波就能把这些元素找出来
-
以这些元素为结尾的最长递增子序列的长度是多少?
回顾我们对dp数组的定义,它记录的正是以每个元素为末尾的最长递增子序列的长度。
以我们举得例子来说,
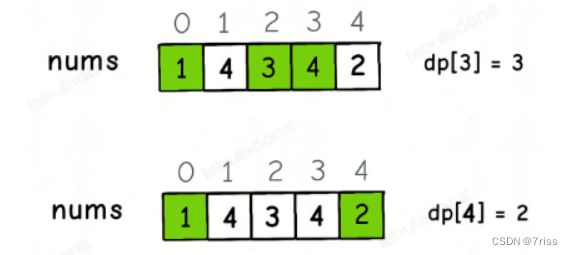
nums[0]和nums[4]都是小于nums[5]的,然后对比dp[0]和dp[4]的值,我们让nums[5]和更长的递增子序列结合,得出dp[5] = 3:代码实现如下:
for (int j = 0; j < i; j++) { if (nums[i] > nums[j]) { dp[i] = Math.max(dp[i], dp[j] + 1); } }当
i = 5时,这段代码的逻辑就可以算出dp[5]。其实到这里,这道算法题我们就基本做完了。 -
但是我们刚才只是算了
dp[5],dp[4],dp[3]这些怎么算呢?类似数学归纳法,你已经可以算出
dp[5]了,其他的就都可以算出来:for (int i = 0; i < nums.length; i++) { for (int j = 0; j < i; j++) { // 寻找 nums[0..j-1] 中比 nums[i] 小的元素 if (nums[i] > nums[j]) { // 把 nums[i] 接在后面,即可形成长度为 dp[j] + 1, // 且以 nums[i] 为结尾的递增子序列 dp[i] = Math.max(dp[i], dp[j] + 1); } } }
-
-
整合代码如下
int lengthOfLIS(int[] nums) { // 定义:dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度 int[] dp = new int[nums.length]; // base case:dp 数组全都初始化为 1 Arrays.fill(dp, 1); for (int i = 0; i < nums.length; i++) { for (int j = 0; j < i; j++) { if (nums[i] > nums[j]) dp[i] = Math.max(dp[i], dp[j] + 1); } } int res = 0; for (int i = 0; i < dp.length; i++) { res = Math.max(res, dp[i]); } return res; }时间复杂度为O(N^2)
如何找到动态规划的状态转移关系?
-
明确dp数组的定义。这一步对于任何动态规划问题都很重要,如果不得当或者不够清晰,会阻碍之后的步骤
-
根据dp数组的定义,运用数学归纳法的思想,假设dp[0…i-1]都已知,求出dp[i],这部完成那么整个题目基本上就解决了
如果无法完成这一步,很可能就是dp数组的定义不够恰当,需要重新定义dp数组的含义。也可能是dp数组存储的信息还不够,不足以推出下一步的答案,需要把dp数组扩大成二维数组甚至三维数组
-
2.3 在leetCode上通过的代码
class Solution {
public int lengthOfLIS(int[] nums) {
int length=nums.length;
int[] dp=new int[length];
//base case
Arrays.fill(dp,1);
for(int i=0;i<length;i++){
for(int j=0;j<i;j++){
//在保证递增的情况下,寻找最长的长度
if(nums[j]<nums[i]){
dp[i]=Math.max(dp[i],dp[j]+1);
}
}
}
//寻找dp中的最大值
int max=0;
for(int k=0;k<length;k++){
max=Math.max(max,dp[k]);
}
return max;
}
}
三、二分查找解法
上面的解法是标准的动态规划,但对最长递增子序列问题来说,这个解法不是最优的,可能无法通过所有测试用例。
而二分查找是更高效的解法
怎么用到二分查找解法?
这个解法的时间复杂度为O(NlogN)
但是这个解法很难想到,所以掌握动态规划解法就行了
最长递增子序列和一种叫做patience game 的纸牌游戏有关,甚至有一种排序方法就叫做 patience sorting(耐心排序)。
现在通过一个简化的例子来理解算法的思路
现在有一排扑克牌,我们像遍历数组那样从左到右一张张地处理这些扑克牌
处理这些扑克牌要遵循以下规则:
只能把点数小的牌压到点数比它大的牌上
如果当前牌点数较大,没有可以放置的堆,则新建一个堆,把这张牌放进去
如果当前牌有多个堆可供选择,则选择最左边的那一堆放置
但是为什么遇到多个可选择的堆时要放到最左边的堆上?
因为这样可以保证牌堆顶的牌有序(2, 4, 7, 8, Q)
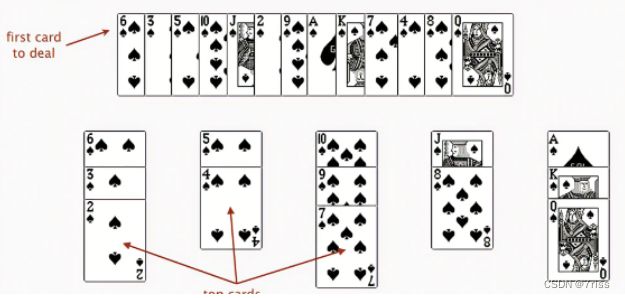
如下图,这些扑克牌会被分成这样的5堆
纸牌A的牌面是最大的,纸牌2的牌面是最小的
按照上述规则执行,可以算出最长递增子序列,牌的堆数就是最长递增子序列的长度
每处理一张扑克牌就是要找到一个合适的牌堆顶来放,牌堆顶的牌有序,这就会用到二分查找,用二分查找来搜索当前牌应放置的位置’
完整的代码如下:
int lengthOfLIS(int[] nums) {
int[] top = new int[nums.length];
// 牌堆数初始化为 0
int piles = 0;
for (int i = 0; i < nums.length; i++) {
// 要处理的扑克牌
int poker = nums[i];
/***** 搜索左侧边界的二分查找 *****/
int left = 0, right = piles;
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else {
right = mid;
}
}
/*********************************/
// 没找到合适的牌堆,新建一堆
if (left == piles) piles++;
// 把这张牌放到牌堆顶
top[left] = poker;
}
// 牌堆数就是 LIS 长度
return piles;
}
四、最长递增子序列的变种(拓展到二维)
354. 俄罗斯套娃信封问题
这道题目其实是最长递增子序列的一个变种,因为每次合法的嵌套是大的套小的,相当于在二维平面中找到一个最长递增的子序列,其长度就是最多能嵌套的信封个数
如何解决在二维数组上找最长递增子序列呢?
前面说的标准LIS算法只能在一维数组中寻找最长子序列,而我们的信封是由(w,h)这样的二维数组对形式表示的,如何把LIS算法运用过来呢?
试着想,我们可以通过w*h计算面积,然后对面积进行标准的LIS算法吗?
但这样的解法是不对的,比如1 * 10大于3 * 3,但是这样的两个信封是无法互相嵌套的
正确的解法是:
先对宽度
w进行升序排序,如果遇到w相同的情况,则按照高度h降序排序;之后把所有的h作为一个数组,在这个数组上计算 LIS 的长度就是答案。如图所示:
为什么这样就可以找到互相嵌套的信封序列呢?
- 首先对宽度w从小到大排序,确保了w这个维度可以互相嵌套,所以我们只需要专注高度h这个维度能够互相嵌套
- 然后两个w相同的信封不能相互包含,所以对于宽度w相同的信封,对高度h进行降序排序,保证二维LIS中不存在多个w相同的信封(因为题目说了长宽度相同也无法嵌套)
完整代码如下:
// envelopes = [[w, h], [w, h]...] public int maxEnvelopes(int[][] envelopes) { int n = envelopes.length; // 按宽度升序排列,如果宽度一样,则按高度降序排列 Arrays.sort(envelopes, new Comparator<int[]>() { public int compare(int[] a, int[] b) { return a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]; } }); // 对高度数组寻找 LIS int[] height = new int[n]; for (int i = 0; i < n; i++) height[i] = envelopes[i][1]; return lengthOfLIS(height); } int lengthOfLIS(int[] nums) { // 见前文 }当然以上两个方法也可以合并,这样就省下了hehight数组的空间
补充知识:Arrary.sort用 Comparator比较器定制排序方式
Arrary.sort()是用于给数组排序的,默认情况下是顺序排序,即从小到大
例如:实现Arrary.sort用 Comparator比较器定制排序方式
在实现之前要注意一点:
Comparator的定义,是用了泛型的。
public interface Comparator<T>{ }泛型本质是引用,是不能传入基本数据类型(如int、long等)的,即T不能为 int 等,即Comparator会报错,要用Integer 代替 int。
而Comparator接口中包含了一个最核心的方法:int compare() ,这个方法是用于定义排序规则的,如下:
int compare(T o1,T o2);compare的参数o1、o2 也是泛型T,即排序的元素也不能是基本数据类型。
由于 compare()比较抽象,所以我们可以这样记:
int compare(T o1, T o2) 是比较o1和o2的大小
如果compare返回值为负数意味着o1比o2小
否则返回为零意味着o1等于o2
返回为正数意味着o1大于o2
实现从小到大排序
public class Test { public static void main(String[] args) { Integer[] arr = {9, 8, 7, 2, 3, 4, 1, 0, 6, 5}; Arrays.sort(arr, new Comparator<Integer>() { @Override public int compare(Integer o1, Integer o2) { return o1-o2; } }); } }当我们需要逆序(大到小排列)的时候,只需要 return o2-o1
即表示数值越大的数compare会认为它越小,数值越小的数compare反而会认为它越大
当然我们实现逆序也可以将按从小到大顺序排序的数组反转即可
public class Test { public static void main(String[] args) { Integer[] arr = {9, 8, 7, 2, 3, 4, 1, 0, 6, 5}; Arrays.sort(arr, Collections.reverseOrder()); } }注意:如果用reverseOrder()的话,数组也是要设置成 Integer的。也是不能用基本数据类型。
用lambda表达式更简介地实现Comparator
public class Test { public static void main(String[] args) { Integer[] arr = {9, 8, 7, 2, 3, 4, 1, 0, 6, 5}; Arrays.sort(arr, (o1,o2)->{return o2-o1;}); } } }用Arrays.sort 进行二维数组排序
要做二维数组排序,实际上就是自己有Comparator来定制
只对二维数组的第一个数排序
即将 二维数组
[(1,9),(2,5),(19,20),(10,11),(12,20),(0,3),(0,1),(0,2)]
经过排序后得到以下二维数组:
[(0,3),(0,1),(0,2),(1,9),(2,5),(10,11),(12,20),(19,20)]
public class Test { public static void main(String[] args) { int[][] arr = {{1,9},{2,5},{19,20},{10,11},{12,20},{0,3},{0,1},{0,2}}; Arrays.sort(arr,new Comparator<int[]>(){ @Override public int compare(int[] o1, int[] o2) { return o1[0]-o2[0]; } }); } }注意:这里的数组不需要设置成Interger[] [],因为int[] 本身就是引用而不是基本数据类型,所以泛型T是可以为 int[] 的
二维数组按第一位数升序排序,若宽度一样按第二位数降序排序
public class Test { public static void main(String[] args) { int[][] arr = {{1,9},{2,5},{19,20},{10,11},{12,20},{0,3},{0,1},{0,2}}; Arrays.sort(arr,new Comparator<int[]>(){ @Override public int compare(int[] o1, int[] o2) { return o1[0]=o2[0]?o2[1]-o1[1]:o1[0]-o2[0]; } }); } }
在leetCode上通过的代码:
如果是用的动态规划会超出时间限制
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-K2PQwzPU-1683776767666)(D:\Development\Typora\img\image-20230511114428889.png)]
class Solution {
public int maxEnvelopes(int[][] envelopes) {
//1.先处理数据,按宽度升序排序,宽度相同,高度降序排序
// Arrays.sort(envelopes, (o1[],o2[])->{return o1[0]==o2[0]?o2[1]-o1[1]:o1[0]-o2[0];});
Arrays.sort(envelopes, new Comparator<int[]>() {
public int compare(int[] a, int[] b) {
return a[0] == b[0] ?
b[1] - a[1] : a[0] - b[0];
}
});
//2.处理完之后对高度找LIS
int length=envelopes.length;
int[] dp=new int[length];
Arrays.fill(dp,1);
for(int i=0;i<length;i++){
for(int j=0;j<i;j++){
if(envelopes[j][1]<envelopes[i][1]){
dp[i]=Math.max(dp[i],dp[j]+1);
}
}
}
//3.找最大值
int max=0;
for(int k=0;k<length;k++){
max=Math.max(max,dp[k]);
}
return max;
}
}
所以要用到最长递增子序列的二分查找解法
class Solution {
public int maxEnvelopes(int[][] envelopes) {
int n = envelopes.length;
// 按宽度升序排列,如果宽度一样,则按高度降序排列
Arrays.sort(envelopes, new Comparator<int[]>()
{
public int compare(int[] a, int[] b) {
return a[0] == b[0] ?
b[1] - a[1] : a[0] - b[0];
}
});
// 对高度数组寻找 LIS
int[] height = new int[n];
for (int i = 0; i < n; i++)
height[i] = envelopes[i][1];
return lengthOfLIS(height);
}
/* 返回 nums 中 LIS 的长度 */
public int lengthOfLIS(int[] nums) {
int piles = 0, n = nums.length;
int[] top = new int[n];
for (int i = 0; i < n; i++) {
// 要处理的扑克牌
int poker = nums[i];
int left = 0, right = piles;
// 二分查找插入位置
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] >= poker)
right = mid;
else
left = mid + 1;
}
if (left == piles) piles++;
// 把这张牌放到牌堆顶
top[left] = poker;
}
// 牌堆数就是 LIS 长度
return piles;
}
}