2020.9月做题记录

八月的做题记录因为是暑假所以鸽掉了。
离联赛真的不远了，要继续努力啊qwq…

week -1

2020.08.30

2020.08.30

今天考试，修了20+次锅，修的我都没有心情做题了…
然后开始消极比赛…
明明08还是有那么多质量高的题目，为什么要选这些题…
结果考后补题的时候又发现了一堆没有修好的锅…
真没想到大家对待出题互测的态度就是这样，唉…

HDU6855 Auto-correction

一道没有任何营养的本身很简单却要输入大模拟+输出方案的dp题。
首先模拟求得$\{b_i\}$序列，然后有个显然的dp。
定义$f_{i,j}$表示现在处理好$a$序列的前$i$个，$b$序列的前$j$个，最小的答案的$pair$为多少(即被替换的数的数量和操作次数)。
显然有:
$$f_{i,j}=\min \{\begin{array}{l}{f}_{i-1,j-1}(a_i=b_i)\\ {\min }_{0\le i^{\prime }<i,0\le j^{\prime }<j}\{f_{i^{\prime },j^{\prime }}+(i-i^{\prime },1)\}\end{array}$$
这是$O(n^4)$的。
上面这个式子我们只需要维护一下前缀最小值就可以做到$O(n^2)$。

HDU6861 Gaming of Co-prime Disallowance

如果知道莫比乌斯反演怎么容斥的话这题就是板子题…
说实话我现在才知道我之前搞的某些容斥是莫比乌斯反演…
考虑反演，我们枚举$d$，我们要计算选择了若干个数后最终这些数的gcd不被$d$整除。
我们可以把所有被$d$整除的$a_i$提出来，然后计算从中挑出$k$个的概率。
设$f(d,k)$即从$d$整除的$a_i$连续选$k$个的概率。
显然$$f(d,k)=\frac{cn{t}_d^{\underline{k}}}{n^{\underline{k}}}$$
那么定义$g_i$表示至多挑$i$个数后所有数的$gcd$变为$1$个概率。
那么有$g_k+=\mu (k)\times f(d,k)$。
最终答案是${\sum }_{i\mathrm{m}\mathrm{o}\mathrm{d}2=0}^{n+1}{g}_i-g_{i-1}$
注意边界$g_{n+1}=1$。

这题还好吧，至少有教育意义:)

tip:有一个非常神奇的错误：printf("%.5f",(x&1));在Linux会输出一堆奇奇怪怪的小数，必须printf("%.5f",(x&1)?1.0:0.0);。

HDU6863 Isomorphic Strings

一道没有任何营养的大暴力题。
$O(\sigma (n)+n\log n)$能过，没了。

CF455D Serega and Fun

明显可以分块套一个链表/队列即可。
看到有用块状链表的…感觉用到这题上面不是很好…
其实用队列维护比较麻烦，不过deque有erase功能…

CF506D Mr. Kitayuta’s Colorful Graph

套路题…
考虑设计两个做法，然后它们拼起来。
考虑到单颜色边数大于 $\sqrt{m}$ 的颜色最多 $\sqrt{m}$个。
因此对于单颜色边数大于 $\sqrt{m}$ 的颜色我们直接分别对每个颜色暴力用并查集维护即可，复杂度$O(n\sqrt{m}\alpha (n))$。
单颜色边数小于 $\sqrt{m}$ 的比较难想。注意到这种情况下涉及到的图中的点数最大为 $O(\sqrt{m})$，那么我们可以直接把涉及到的点的两两之间的答案直接求出来存在 map 中，这样做是 联通块大小的平方的复杂度。
这样做看似会达到$O(m^2)$的复杂度，但是可以证明对于 $m$ 的一个划分 $a_i$ ，即:
$$\{\begin{array}{l}{\sum }_{i=1}^k{a}_i=m\\ a_i<\sqrt{m}\end{array}$$
一定满足 ${\sum }_{i=1}^k{a}_i^2<m\sqrt{m}$（直接放缩就可以证明） 。
因此这个算法的复杂度实际上是$O(m\sqrt{m}\alpha (n))$。
总复杂度:$O(m\sqrt{m}\alpha (n)+n\sqrt{m}\alpha (n))$。
但是，有一个本质差不多的暴力也能够直接通过这道题目，详见大佬博客。

week 1

2020.08.31-2020.09.06

又开学了…

2020.08.31

由于一些原因，总结第二天写的…

2020.09.01

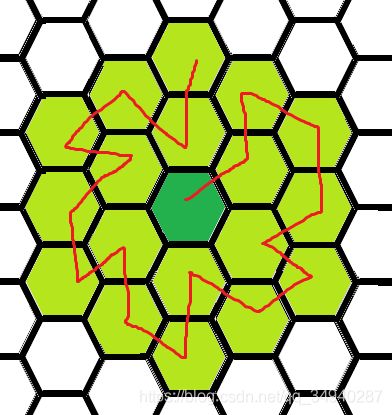
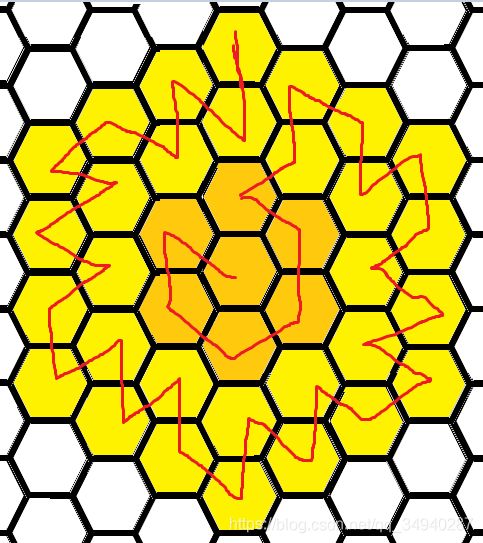
HDU6862 Hexagon

$n$为奇数的构造方案:

$n$为偶数的构造方案:

以下是简短的代码:

void print(int x){
	printf("213");
	for(int i=1;i<x;i++)printf("42");
	printf("4");
	for(int i=1;i<=x;i++)printf("53");
	printf("5");
	for(int i=1;i<=x;i++)printf("64");
	printf("6");
	for(int i=1;i<=x;i++)printf("15");
	printf("1");
	for(int i=1;i<=x;i++)printf("26");
	printf("2");
	for(int i=1;i<=x;i++)printf("31");
}
void solve(int n){
	if(n%2==0)printf("643216");
	for(int i=(n%2==0)?2:1;i<n;i+=2)print(i);
}

HDU6864 Jumping on a Cactus

首先对于树的情况，考虑我们现在先随便排顺序，再考虑是否合法。我们可以把条件转化为任意一颗子树的根都必须先比它的儿子出现。
那么可以得到树的答案就是$n!{\prod }_{i=1}^n\frac{1}{si{z}_i}$。
对于仙人掌的情况，我们对于每个不在环上的点还是乘上后面那个系数，对于环我们单独讨论乘上什么系数。
这里一定要注意到原题有$d_{u_i}\ne d_{v_i}$这个条件，这意味着这是一个偶环仙人掌。
那么我们可以先建出原图的BFS生成树，这样我们的环的$d$值一定会随深度的增大而增大。这是整道题目最核心的思想。
考虑对环上的点进行dp，注意到在BFS生成树上的环的横叉边一定位于这个环的底部，并且把环的底部的一个点删去之后两边均匀的分成了两个部分且都必须遵守从下往上取的顺序关系。
因此我们考虑一个$O(n^2)$的dp，定义$f_{i,j}$表示当前环左边已经从下往上取了$i$个数，右边已经从下往上取了$j$个数的限制系数之和。
那么有$f_{i,j}=(f_{i-1,j}+f_{i,j-1})\frac{1}{su{m}_{i,j}}$。
这里$su{m}_{i,j}$表示已经在环上取了的点和其延伸出去的所有点的大小之和，这个可以比较方便的处理出来。
复杂度:$O(n^2)$，由于环的大小比较小因此常数很小。

tip:多测太恶心人了…
为什么我现在从来没有存图的head[x]的数组必须清零的印象…
以后多组测试数据最好都清零或者把两个样例多测几遍…

[LOCAL] 解析电车(electric)

已知 $n$ 个点 $m$ 条边的无向连通图，对于三元组 $(u,v,r)$ 表示 $u,v$ 之间连接一阻值为 $r$ 的电阻
给定 $S,T$ 求出 $S,T$ 间的等效电阻

就是个物理题…
假设 $S$ 流入 $1A$ 电流，设每个点 $i$ 的电势为 ${\phi }_i$。
这样我们最终的答案就是 ${\phi }_S$ 。
根据基尔霍夫电流定律，对于每个点$u$均满足:
$$\sum _v\frac{{\phi }_u-{\phi }_v}{R_{u,v}}=[u=S]-[u=T]$$
但是光靠这个是解不出来了。
我们还需要 ${\phi }_T=0$ 就可以了。

2020.09.02

[2020牛客暑期多校-第五场] C.Easy

首先考虑一个 $O(n^4)$ 的动态规划:
定义$f_{u,v,k}$为当前${\sum }_{i=1}^k{a}_i=u,{\sum }_{i=1}^k{b}_i=v$，可以考虑用前缀和的套路进行转移。
这种二维转移很容易让我们想起走网格图之类的经典模型，但是${\prod }_{i=1}^k\min (a_{,}{b}_i)$这个代价很难以转化成组合意义。
这里用到的一个很关键的技巧：对于走网格图一类经典模型，我们同样可以把它写成生成函数的形式。
若我们求的是划分的方案数，那么生成函数是:
$$(x+x^2+\cdots +x^n{)}^k(y+y^2+\cdots +x^m{)}^k$$
我们需要的即是第$x^n{y}^m$项的系数。
那么对于本题，我们可以把代价看成在这个基础上选择若干个划分在同一块中的 $x$和$y$合并起来的方案数，即：
$$(x+x^2+\cdots +x^u{)}^k(y+y^2+\cdots +x^v{)}^k(1+xy+\cdots +(xy{)}^{n-k}{)}^k$$
我们可以直接组合数计算出$x^n{y}^m$的系数。
复杂度:$O(Tn)$。

LOJ6584「ICPC World Finals 2019」Hobson 的火车

一看到这种模型就知道是什么无脑大模拟之类的东西…
事实上对于环我们单独考虑环上差分，树的部分直接树上差分即可。
实现上可以通过桶之类的东西做到 $O(n)$，但是直接倍增 $O(n\log n)$ 也没有什么区别。

tip:一定要注意空间上的开销问题。

[TJOI2013]拯救小矮人

考虑交换论证得到原序列可以按照 $a_i+b_i$ 的顺序排列一定最优。
但是我们并不清楚当前矮人是否会被安排逃出井中。
对于$O(n^2)$的数据我们考虑通过dp来解决。
我们考虑一开始先把所有人按顺序堆在一起，然后从上到下让每个人依次逃出洞穴，如果发现有人逃不出这个洞时，我们就拿一个已经逃出洞且$a_i$最大的一个人拉回去，让这个人逃出洞中，可以发现这样一定可行且答案一定不会变得更劣，因此会得到最优解。
实现的话用一个优先队列即可。
复杂度：$O(n\log n)$。

2020.09.03

[SHOI2016]随机序列

注意到我们对于一个形如$a_1\times a_2\cdots \times a_{k_1}+b_1\times b_2\cdots \times b_{k_2}+\dots$这样的序列，我们总能找到恰好一个相反的序列$a_1\times a_2\cdots \times a_{k_1}-b_1\times b_2\cdots \times b_{k_2}-\dots$使得结果抵消为$a_1\times a_2\cdots \times a_{k_1}$。
那么我们就可以直接维护这个序列的前缀积$S_i$，答案就是$S_n+{\sum }_{i=1}^{n-1}{S}_i\times 2\times 3^{n-i-1}$。
考虑用线段树维护当前节点内的前缀积$pro{d}_x$，当前节点内的前缀积的和$su{m}_x$。
那么有:
$$\begin{gathered} pro{d}_x=pro{d}_{lc}\times pro{d}_{rc} \\ su{m}_x=su{m}_{lc}+pro{d}_{lc}\times su{m}_{rc} \end{gathered}$$
写一个支持单点修改的线段树即可。
复杂度:$O(n\log n)$

[2020牛客暑期多校-第五场]A.Portal

我们可以把原问题等价为两个人在图上依次按顺序遍历若干个点$d_i$，其中一个人可以在任意时刻瞬移到另一个人当前所在的位置，求最小遍历路径长度。
定义$f_{i,a,b}$表示完成遍历了前$i$个点，现在第一个人在点$a$，第二个人在点$b$。
每次我们从$i-1$转移至$i$，那么其中一个人需要走到$d_i$，我们设其为$c$。
然后分两种情况转移即可：

• 选择一个人直接走到$c$点，即$f_{c,b}=\min \{f_{a,b}+di{s}_{a,c}\}$和$f_{a,c}=\min \{f_{a,b}+di{s}_{b,c}\}$。
• 还是选择一个人走到$c$点，考虑另一个人会在行走时瞬移到某一个点 $d$ ，那么有$f_{c,d}=\min \{f_{a,b}+di{s}_{a,d}+di{s}_{d,c}\}$和$f_{d,c}=\min \{f_{a,b}+di{s}_{b,d}+di{s}_{d,c}\}$。

转移的时候我们 $a,b$ 之中只需要枚举一个数，另外一个显然是 $d_{i-1}$ ，转移过程中我们需要枚举 $d$ ，因此总的复杂度是$O(n^{2}k)$。

[2020牛客暑期多校-第五场]B.Graph

显然加的边的 $pair$ 时边权相同。
考虑dfs处理$d_x$表示$x$到根的边的异或和。
那么一条$(u,v)$的边权就是$d_u\oplus d_v$，然后我们求一颗最小生成树即可。
然后就是最小异或生成树模板题[CF888G Xor-MST]。
复杂度:$O(n{\log }^2{a}_i)$。

tip: 注意复习以前做过的经典模型。

2020.09.04

莫比乌斯反演练习：

P3935 Calculating
CF439E Devu and Birthday Celebration
CF547C Mike and Foam
CF839D Winter is here
P2257 YY的GCD
P2522 [HAOI2011]Problem b
P3172 [CQOI2015]选数
P3327 [SDOI2015]约数个数和
P3455 [POI2007]ZAP-Queries
P4450 双亲数
P6055 [RC-02] GCD
P1829 [国家集训队]Crash的数字表格 / JZPTAB
P3312 [SDOI2014]数表

其实算是很套路的…
一天AC了十几道题目看似高效实际上代码长得都差不多…(突然想到莫队)

2020.09.05

早上模拟赛又自闭了。
由于某些原因隐藏了题目来源。
题目质量比较一般…

2020.09.06

[LOCAL]异或帽子（hat）

由于 $n$ 是偶数，因此将所有 $b_i$ 异或起来就是所有 $a_i$ 的异或和。
然后我们依次求 $a_i$ 即可。

[LOCAL]传话游戏（string）

$$\{\begin{array}{l}{f}_i=f_{i-1}(s_i=s_{i-1})\\ f_i=f_{i-1}+f_{i-2}(s_i\ne s_{i-1})\end{array}$$

tip:注意 $f_1$ 需要特判，考试的时候我没特判导致访问到了 $f_{-1}$ ，还好由于某些原理（比如你int a[100],x;，那么a[-1]就是x）这个指针的位置上的值一定是0，就没错…以后一定要注意这个问题。

[LOCAL]全球覆盖（globe）

容易发现横纵方向互相独立，我们可以单独考虑再乘起来。
这样问题就变成了一个线段覆盖问题。
虽然总共的选择方案是$2^n$，但是发现对于一个中间没有任何线段端点的一段线段，它有且仅会对应一个选择方案。因此合法的选择方案最多是 $2n$ 的。
直接dfs+剪枝即可得到一个$O(n^2)$的做法，对于相同选择方案的一段我们采用hash+map来合并。
但是注意到我们仅会在该线段的端点修改选择方案的状态，因此我们直接从左到右递推即可做到 $O(n\log n)$。

tip:为了避免卡常，最好使用$unordered\_map$。

[LOCAL]幂次序列（sequence）

这种题目显然考虑分治，考虑计算在区间 $[l,r]$ 跨过分治中心的的合法区间数，注意到最终求到的数一定最多比在当前区间的最大数$mx$大$\log n$。这样我们就可以把分治中心设为$mx$暴力枚举最终答案计算区间数了。
至于计算方案数的细节…特别多…我不想提…反正注意计算时暴力枚举长度小的一边计算是$O(n\log n)$的即可。
如果我们用map复杂度是$O(n{\log }^{3}n)$，但是使用$unordered\_map$就是 $O(n{\log }^{2}n)$。

tip:考试的时候$a_i\le 30$的$O(n{\log }^{2}n)$二分查找，其余的$O(n^2)$暴力+大力剪枝直接AC可还行…
当然这种写起来恶心死人的题目还是乱搞比较好:)
找到一个有趣的质数:$1145146987$，分享一下qwq。

week 2

2020.09.07-2020.09.13

2020.09.07

杜教筛入门

P4844 LJJ爱数数

2020.09.08

读错题了…然后就爆炸+垫底了…

[LOCAL]召唤（summon）

其实结论就是直接暴力循环比较即可。
但是明显用hash一段一段的判断相等比暴力匹配要稳的多。
复杂度:$O(n+m)$

[LOCAL]卫队（guard）

看成异或和，然后成功自闭了。
如果是或和的话我们直接在笛卡尔树时维护一个 $O(\log a_i)$ 的tag即可。
时限不好的会由于题目要求32MB会爆栈空间，当然我没有管这个问题。
复杂度:$O(n\log a_i)$

[LOCAL]排队（queue）

结论是这个后缀排序等价于 $\{c_i\}$ 的后缀排序。
其中 $\{c_i\}$ 为${\min }_{j,j>i,s_i=s_j}\{j-i\}$。
其实我们也可以不用这个结论利用后缀数组或SAM的一些函数直接进行排序。
复杂度:$O(n\log n)$。

2020.09.09

P3700 [CQOI2017]小Q的表格

感觉是CQOI里面出的最好的题目之一(?)。

CF1375G Tree Modification

2020.09.10

[LOCAL]镜子（mirror）

挺简单一道题，然而我做了1h…

[LOCAL]排水（water）

[LOCAL]充电（charge）

2020.09.11

CF1391E Pairs of Pairs

2020.09.12

真·NOIP模拟赛。

[LOCAL]求和（sum）

直接莫比乌斯反演可以得到一个 $O(n\log n)$ 的做法，但是无法通过 $n\le 5\times 10^7$ 的数据。
注意到原式还可以表达为：
$$\sum _{d=1}^n(\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }\sigma (jd){)}^2$$
我们只需要用Dirichlet 后缀和即可 $O(n\log \log n)$ 预处理${\sum }_{j=1}^{\lfloor \frac{n}{d}\rfloor }\sigma (jd)$，然后 $O(n)$ 计算即可。

[LOCAL]摸鱼（fish）

发现无论怎么选加上一个直径一定不会使答案变劣，因此我们考虑首先加入直径，接下来的 $B$ 集合的权值一定会递减，$A$ 集合的权值一定会递增。
根据经典结论，我们每次加入一个点，离它最远的点一定包含直径端点中的一个。
因此我们只需要用剩下点的按距离从大到小排序依次加入，取最大权值即可。
复杂度:$O(n\log n)$

[LOCAL]舟游（arknights）

method 1

首先容易发现所有当前拥有卡片的状态可以 $O(4^n)$ 来表示。
那么定义 $d{p}_{S,i}$ 表示当前拥有卡片状态为 $S$ ，现在某轮抽卡已经进行了 $i$ 次的期望步数。
那么容易发现这个转移会呈现出若干个大小为 $m$ 的不相交的环，因此我们对每个环单独解出它的值即可。
具体来说我们可以把每个 $d{p}_{S,i}$ 写成 $p_i\times d{p}_{S,i-1}+q_i$，那么最终我们可以吧每个式子都写成 $d{p}_{S,i}=x_{i}d{p}_{S,0}+y_i$ 的形式。
而我们可以通过 $d{p}_{S,0}$ 自己和自己的关系解出 $d{p}_{S,0}$ ，然后我们再依次递推即可。
复杂度: $O(4^{n}nm)$。

method 2

其实本题是一个 min-max 反演的经典模型(而且那题也有这两种做法…)。
我们可以根据 min-max 反演把本题转化为：
$$E[\max (S)]=\sum _{T\subseteq S}(-1{)}^{|T|+1}E[\min (T)]$$
那么我们只需要求每一个物品子集中最先被选中的期望次数为多少。
容易计算出我们一轮都不会选择到任何属于该集合中的数的概率为 $P=(1-{\sum }_{i\in T}{p}_i{)}^{m-1}\times (1-{\sum }_{i\in T}{q}_i)$，那么易得:
$$\begin{gathered} E[\min (T)]=1+P\times E[\min (T)] \\ E[\min (T)]=\frac{1}{1-P} \end{gathered}$$
然后我们用 dfs 枚举状态计算即可。
复杂度:$O(4^n\log m)$。

[LOCAL]选课（class）

这怕是整场考试最大的一个败笔，2^n暴力直接70，正解无脑线段树优化建图。
说白了就是个码农题…
显然我们可以用 2-SAT 来判断这个问题，但是边数最多是 $O(m^2)$ 级别的。
显然我们接下来考虑线段树优化建图，我们正着和倒着建两颗线段树，我们在叶子连上要被限制的点（具体来说我们只需要两个端点连到叶子上即可），对于区间的限制$[l_i,r_i]$我们连到线段树上的节点即可。
但是这样明显有一个问题，就是它可以自己向自己连边。在 2-SAT 是一个很难处理的问题。
为了防止这种情况，我们现在只连$[l_i+1,r_i-1]$的区间限制，那么区间端点恰好为 $l_i$ 或 $r_i$ 的区间不会被限制，因此我们单独把这些区间提出来做一个经典的前缀&后缀限制即可。
复杂度:$O(n\log n)$。(常数确实大…)

2020.09.13

在补前几天的锅qwq…

week 3

2020.09.14

2020.09.15

怎么感觉CF的难度评分变水了…

CF1401D Maximum Distributed Tree

贪心即可。

CF1400E Clear the Multiset

这不是经典题目吗…连ST表都不用…

CF1401F Reverse and Swap

看完题目想到tire树，但是要区间查询因此我们把它想成一颗线段树。
对于左右儿子交换的情况我们只需要用一个数组记录一下每次往那边走即可。
复杂度:$O(n\log n)$。

2020.09.16

以为自己已经会莫比乌斯反演了…结果是假相。

51nod1584 加权约数和

求:$$\sum _{i=1}^n\sum _{j=1}^n\max (i,j)\cdot \sigma (i\cdot j)(\mathrm{m}\mathrm{o}\mathrm{d}10^9+7)$$
$T\le 5\times 10^4,n\le 10^6$。

首先可以研究${\sigma }_0(i\cdot j)={\sum }_{x|i}{\sum }_{y|j}[gcd(x,y)=1]$的结论原理推出:
$$\sigma (i\cdot j)=\sum _{x|i}\sum _{y|j}\frac{i}{x}\cdot y[gcd(x,y)=1]$$
注意到$\max (i,j)$不是很好弄，我们先只考虑 $i<j$ 的情况。
得到:
$$\sum _{i=1}^n\sum _{j=i+1}^{n}i\cdot j\sum _{x|i}\sum _{y|j}\frac{y}{x}[gcd(x,y)=1]$$
考虑对$[gcd(x,y)=1]$莫反:
$$\sum _{i=1}^n\sum _{j=i+1}^{n}i\cdot j\sum _d\mu (d)\sum _{d|x,x|i}\sum _{d|y,y|j}\frac{yd}{xd}$$
注意到$i,j$要满足 $d|i,d|j$，因此我们可以把 $d$ 提到外面来。
$$\begin{gathered} \sum _d\mu (d)d^2\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=i+1}^{\lfloor \frac{n}{d}\rfloor }i\cdot j\sum _{x|i}\sum _{y|j}\frac{y}{x} \\ \sum _d\mu (d)d^2\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=i+1}^{\lfloor \frac{n}{d}\rfloor }j\left(\sum _{x|i}\frac{i}{x}\right)\left(\sum _{y|j}y\right) \\ \sum _d\mu (d)d^2\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=i+1}^{\lfloor \frac{n}{d}\rfloor }j\cdot \sigma (i)\cdot \sigma (j) \\ \sum _d\mu (d)d^2\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }j\cdot \sigma (j)(\sum _{i=1}^{j-1}\sigma (i)) \end{gathered}$$
令$S(n)={\sum }_{i=1}^n\sigma (i)$。
那么有:
$$\sum _d\mu (d)d^2\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }j\cdot \sigma (j)\cdot S(j-1)$$
我们再取消 $i<j$ 的限制，注意需要加上 $i=j$ 的情况，得到答案为：
$$\sum _d\mu (d)d^2\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }j\cdot \sigma (j)\cdot (S(j)+S(j-1))$$
显然我们可以使用数论分块来解决这个问题，但是因为常数太大 $O(T\sqrt{n})$ 过不去…
考虑离线预处理这个式子，令 $G(j)=j\cdot \sigma (j)\cdot (S(j)+S(j-1))$，然后我们交换式子:
$$\sum _{j=1}G(j)\sum _{d,jd\le n}\mu (d)d^2$$
这个就可以 $O(n\log n)$ 预处理了…

51nod1594 Gcd and Phi

随便反演一下…就没了…

51nod1355 斐波那契的最小公倍数

其实是一个结论题…
接下来一堆引理:

引理1:$gcd(f_{n-1},f_n)=1$。
证明:$gcd(f_{n-1},f_n)=gcd(f_{n-1},f_{n-1}+f_{n-2})=gcd(f_{n-2},f_{n-1})=...=gcd(f_1,f_2)=1$

引理2:$gcd(f_a,f_b)=f_{gcd(a,b)}$。
证明:考虑转化为证明$gcd(f_a,f_b)=gcd(f_{a+b},f_b)$即可利用辗转相除的性质进行证明。
根据引理1可得:
$$gcd(f_{a+b},f_b)=gcd(f_{a-1}{f}_b+f_a{f}_{b+1},f_b)=gcd(f_a{f}_{b+1},f_b)=gcd(f_a,f_b)$$

引理3:$lcm\{S\}={\prod }_{T\ne \varnothing ,T\subseteq S}\gcd \{T{\}}^{(-1{)}^{|T|+1}}$。
简单证明:考虑对于每一个质因子 $p_i$ ，$lcm$ 是取集合中次数最高的幂，$gcd$ 是取集合中次数最低的幂，这显然符合 $min-max$ 容斥的条件，那么我们再把每个质因子的情况和在一起即为上式。

那么对于本题而言，利用上面的引理，我们需要求的就是:
$$lcm\{S\}=\prod _{T\ne \varnothing ,T\subseteq S}{f}_{\gcd \{T\}}^{(-1{)}^{|T|+1}}$$
考虑计算贡献，即为:
$$lcm\{S\}=\prod _d{f}_d^{{\sum }_{T\ne \varnothing ,T\subseteq S}[\gcd \{T\}=d](-1{)}^{|T|+1}}$$
令 $a_d={\sum }_{T\ne \varnothing ,T\subseteq S}[\gcd \{T\}=d](-1{)}^{|T|+1}$ 考虑对其莫比乌斯反演，那么我们再定义 $b_d={\sum }_{T\ne \varnothing ,T\subseteq S}[d|\gcd \{T\}](-1{)}^{|T|+1}$，我们只需要求出 $b_d$ 即可通过反演求出 $a_d={\sum }_{d|p}\mu (\frac{p}{d})b_p$ 。
考虑对于 $b_d$ 可以选择的数的个数为 $g_d={\sum }_{d|p}cn{t}_p$。
那么产生 -1 （$|T|$为偶数）的贡献的会有 $2^{g_d-1}-1$ （除去空集）个，产生 1 贡献的会有 $2^{g_d-1}$ 个，那么当 $g_d>0$ 时，$b_d$ 的值就会恒为1 。
那么 $b_d$ 就可以表示为 $b_d=[g_d>0]$。
这样我们就可以 $O(n\log n)$ 求出 $b_d$ 然后反演求出 $a_d$再算式子的值即可。
复杂度:$O(n\log n)$（这里的 $n$ 指值域）。

2020.09.17

P4240 毒瘤之神的考验

毒瘤题。

2020.09.18

忘了干了些什么了

2020.09.19

真是一道好的CSP模拟赛，前两题PJ难度，后两题完全不可做…区分度全在卡常和挂题上面了…比省选更逆向区分的题…
出题人写题解也很用心呢…

[LOCAL]礼物（gift）

Emmm…min-max容斥板题都来了…
$$E[S]=\sum _{T\ne \varnothing ,T\subseteq S}(-1{)}^{|T|+1}\frac{1}{{\sum }_{i\in T}{p}_i}$$
$O(2^n)$ 枚举即可，做完了。
事实上状压dp也可以解决做这个问题…

[LOCAL]战争（war）

题目描述特别长一大串
注意到每轮人数都会减半，模拟即可。
复杂度:$O(n\log n)$

[LOCAL]坚果（nuts）

2020.09.20-21

[LOCAL]爬树（tree）

码农题…码了三个中午都没码完…