【区块链】BLS门限签名介绍及实现

基础知识

参考：BLS数字签名算法介绍及拓展

传统BLS - 实现步骤

1.初始化

• $G_1,G_2$ 是阶为 $p$ 的 乘法循环群 。生成元分别是 $g_1,g_2$

• $e$ 是 双线性映射:G1 * G2 -> GT ,

• 安全$hash$函数:h:{0,1}*-> G1

• 公开参数是$(G_1,G_2,G_T,e,g_1,g_2,p,h)$

2.密钥生成

(1) 选择一个随机数$x\in Z_P$，私钥$S_K=x$ (secret key),计算公钥$P_K=v=g_2^x\in G_2$

3.签名

对消息$M$签名：$sig=h(M)\ast x$

4. 验签

验证等式是否成立：
$e(sig,g_2)=e(h(M),v)$

---

BLS门限签名 - 实现步骤

原理

最简单的实现门限签名的方式就是：SSS（Shamir Secret Share）

---

SSS 的核心是：拉格朗日插值法

拉格朗日插值法：
已知一条$n-1$次曲线上的$n$个点$(x_1,y_1),(x_2,y_2),....,(x_n,y_n)$ .可以使用拉格朗日插值法恢复这条曲线方程，具体如下:
$y=\frac{(x-x_2)(x-x_3)...(x-x_n)}{(x_1-x_2)(x_1-x_3)...(x_1-x_n)}{y}_1+\frac{(x-x_1)(x-x_3)...(x-x_n)}{(x_2-x_1)(x_2-x_3)...(x_2-x_n)}{y}_2+...+\frac{(x-x_1)(x-x_2)...(x-x_{n-1})}{(x_n-x_1)(x_n-x_2)...(x_n-x_{n-1})}{y}_n$

---

举个现实例子： 要实现 m of n 秘密分享。 取 m=3，n=4 。

1. 先任意选择一条 t -1=2 次曲线，以这条曲线在 x=0 处的值作为秘密。
2. 然后任意取出曲线上的 n = 4 个点 (1,2),(2,5), (3,10),(4,17) 后，任选其中三个点后恢复出来的曲线是一样的。
3. 因此，我可以将这四个点（横坐标分别是 1、2、3、4）发送给四个不同的人，这样就是一个 3-of-4 的秘密分享了。

---

有了以上知识，应该可以理解基于 BLS 签名的门限签名算法 。

门限签名定义

门限签名的通俗理解是:在一个签名者群体中，有超过 m (门限) 个签名者对一条消息进行签名就可以得到这个群体对这条消息的签名，并且认为 这个群体 对这条消息进行了验证。

• 超过 m个签名者的不同子集生成的签名是一样的，且任何人都可以验证。
• 由门限签名的性质可知，少于 t 个签名者的群体是得不到群体签名的。

实现步骤

1. 初始化（一样）

• $G_1,G_2$ 是阶为 $p$ 的 乘法循环群 。生成元分别是 $g_1,g_2$

• $e$ 是 双线性映射:G1 * G2 -> GT ,

• 安全$hash$函数:h:{0,1}*-> G1

• 公开参数是$(G_1,G_2,G_T,e,g_1,g_2,p,h)$

2. 密钥生成

这步由 密钥生成中心 完成

（1）密钥生成中心，选择系统主私钥，计算系统主公钥。

• 系统主私钥：$MSK=x$，其中$x$为系统选择的随机数；
• 系统主公钥：$MPK=v=g_2^x\in G_2$

（2）分别计算 节点 的 私钥 和公钥 。

• 随机选择一个 $Z_P$上的 $t-1$ 阶多项式 $P$, 满足 $P(0)=x$, 计算$x_i=P(i)$，
• 签名者$u_i$的私钥：$x_i$,
• 签名者$u_i$的公钥：$v_i=g_2^{x_2}$

（3）公开 主公钥$MPK$ 及所有用户的公钥

3.签名

（1）用户$u_i$计算对消息$M$签名：${\sigma }_i=h(M{)}^{x_i}$；
（2）广播${\sigma }_i$；
（3）用户间签名验证：用户$u_i$收到了来自$u_j$的签名 ${\sigma }_j$后，首先验证签名的正确性:$e({\sigma }_j,g_2)=e(h(M),v_j)$,如果签名正确则记录下来；
（4）待收集到 t 个不同用户的正确签名后，用户计算完整的签名: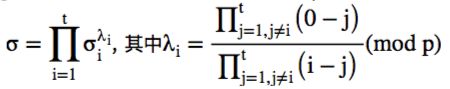
由拉格朗日差值公式可知，任意 t 个用户所产生的完整签名相同

4.验证

$e(\sigma ,g_2)?=e(h(M),MPK)$

代码实现

关于JPBC库安装，可在B站看到相关视频

package com.CYQ.signatures.bls;

import it.unisa.dia.gas.jpbc.Element;
import it.unisa.dia.gas.jpbc.Field;
import it.unisa.dia.gas.jpbc.Pairing;
import it.unisa.dia.gas.plaf.jpbc.pairing.PairingFactory;

//BLS签名（单个）
public class BLS {

    public static void main(String[] args){
        // 初始化
        Pairing bp = PairingFactory.getPairing("a.properties");
        Field G1 = bp.getG1();
        Field Zr = bp.getZr();
        Element g = G1.newRandomElement();
        Element x = Zr.newRandomElement();//私钥
        Element g_x = g.duplicate().powZn(x);//公钥


        //签名
        String m = "message";//签名的消息！
        byte[] m_hash = Integer.toString(m.hashCode()).getBytes();
        Element h = G1.newElementFromHash(m_hash, 0, m_hash.length);
        Element sig = h.duplicate().powZn(x);//签名

        //验证
        Element pl = bp.pairing(g, sig);//g ,sig均为公共参数
        Element pr = bp.pairing(h, g_x);//h,公钥均为公共参数
        if (pl.isEqual(pr))
            System.out.println("Yes");
        else
            System.out.println("No");
    }
}

此文章参考了CSDN上多位博主的文章，可以看作一篇总结文章，此处难以一一列举，望见谅。

如若侵权，请联系，会删除的！

参考：
1、拉格朗日中值定理