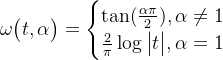Alpha稳定分布噪声特性、产生方法及其仿真

前言

        稳定分布(Alpha Stable Distribution)是一种广义的高斯分布，是高斯分布的推广，即高斯分布仅是它的一个特例。事实上，稳定分布是唯一一种满足广义中心极限定理的分布，即无限多个可能方差无限大的独立分布的随机变量之和的极限分布是稳定分布，很多不满足经典的中心极限定理的数据都可以用稳定分布来描述。同时，现实场景中有很多由非热噪声声源引起的噪声不能很好地用高斯分布进行表示，因此在仿真过程中很多非高斯噪声场景一般都用加性稳定分布噪声进行表示。

        稳定分布是一类非常重要的非高斯随机分布，其最重要的两个特征是概率分布上的稳定性和概率密度函数拖尾较厚。所以，如果某种物理现象即满足稳定性又有较厚拖尾，那么稳定分布就是一种可用的模型。事实上，稳定性是一种非常自然的假设，许多常见的物理过程都具有稳定性;另外，学者们也发现了越来越多的物理现象具有较厚的统计拖尾。由此，稳定分布为不同领域的许多研究提供了非常有用的模型，并且已广泛应用于物理学、水文学、经济学、生物学及信息科学中。

        因为稳定分布噪声与本人研究方向应用场景有点关联，在此做一个简单的记录。

Alpha稳定分布定义及各参数意义

        稳定分布最常用的是根据其特征函数给出的，因为除了少数几个特例外，稳定分布的概率密度函数不存在封闭的表达式，因此通过特征函数(关于特征函数有不清楚的可以参考随机变量的特征函数及应用)定义更为方便，稳定分布的特征函数可表示为：

其中：

 

        从特征函数中可看出，该特征函数由、、及这四个特征参数确定，且有，，， 。这四个参数的物理意义如下所示：

1、特征指数，描述了稳定分布的冲击程度，同时也可以度量分布函数拖尾的厚度。值越小，脉冲性越强，对应分布的拖尾越厚，相反，随着值的增大，分布的冲击程度降低，分布的拖尾也越薄。

2、对称参数，描述了稳定分布的扭曲程度。

3、比例参数，描述了稳定分布变量偏离其均值的程度。

4、位置参数，对于对称稳定分布而言，当时，为均值，当时，为中值。

        特别的是，当时，该分布变为高斯分布，当，时该分布变为柯西分布。当，时该分布变为皮尔逊分布。

        对于标准对称稳定分布来说，由于不存在有限的二阶矩，其方差也就变的没有意义，因此一般加性稳定分布噪声场景下均采用混合信噪比对稳定分布噪声进行度量，有：

其中和分别表示信号的方差和噪声的分散系数。

Alpha稳定分布噪声的产生

        对稳定分布的描述存在着不同的参数系,就随机变量的产生而言,重要的有三种参数系:标准参数系, 参数系与参数系。其中标准参数系为文献中最为常用的参数体系，其四个参数具有明确的意义，但是其分布函数在，处的不连续性给其具体的应用造成了麻烦；参数系提出的主要目的是利于理论分析与推导；参数系表征的稳定分布的特征函数，概率密度函数和累积分布函数关于所有的四个参数均连续。

        参数系的四个参数中，参数与参数同标准参数系所定义的参数相同，而同的关系为：

        参数系的四个参数中除外的三个参数和标准参数系所定义的参数相同，与具有如下关系：

这三种分布的特征函数及其他参数可参考文末参考文献。

定理：若为上的均匀分布，是一个均值为1的指数分布的随机变量，并且和相互独立，则有：

        在给定稳定分布四参数的情况下，服从稳定分布的随机序列产生步骤如下：

1、通过参数系参数转换公式将标准参数系下的参数变成参数系下的参数。

2、应用定理，得到。

3、作变换产生随机变量。

4、令，可得：

因此，当时，需作修正以得到正确的。

function [outputArray] = alpha_dist(inputArray,alpha,beta,gamma,a,msnr)
%%SaS条件下，beta为0，a为0，gamma为1，alpha为[1,2]，在浅海条件下
%%alpha:00,比例参数，另一文中为sigma
%%a:位置参数，另一文中为miu0
if sum(imag(inputArray)) == 0
    comp_flag = 1;%%实数
else
    comp_flag = 2;%%复数
end
arrayLen = length(inputArray);
k_alpha = alpha-1+sign(1-alpha);
if alpha ~= 1
    beta2 = 2*atan(beta*tan(pi*alpha/2))/(pi*k_alpha);
    gamma2 = gamma*(1+beta^2*(tan(pi*alpha/2)^2))^(1/(2*alpha));
else
    beta2 = beta;
    gamma2 = 2*gamma/pi;
end
w = exprnd(1,arrayLen,1)';
gamma0 = -pi/2*beta2*k_alpha/alpha;
gamma1 = -pi/2*ones(1,arrayLen)+pi*rand(comp_flag,arrayLen);
x = zeros(comp_flag,arrayLen);
if alpha ~= 1
    for ik = 1:arrayLen
        for jk = 1:comp_flag
            x(jk,ik) = sin(alpha*(gamma1(jk,ik)-gamma0))/(cos(gamma1(jk,ik))^(1/alpha))*(cos(gamma1(jk,ik)-alpha*(gamma1(jk,ik)-gamma0))/w(ik))^((1-alpha)/alpha);
        end
    end
else
    for ik = 1:arrayLen
        for jk = 1:comp_flag
            x(jk,ik) = (pi/2+beta2*gamma1(jk,ik))*tan(gamma1(jk,ik))-beta2*log10(w(ik)*cos(gamma1(jk,ik))/(pi/2+beta*gamma1(jk,ik)));
        end
    end
end
y = gamma2*x;
if alpha ~= 1
    u = y+a*ones(1,arrayLen);
else
    u = y+a+2/pi*gamma*beta*log(2*gamma/pi)*ones(1,arrayLen);
end
amp_lvl = sqrt(10^(msnr/10)*gamma);
if comp_flag == 1
    outputArray = inputArray+u/amp_lvl;
else
    outputArray = real(inputArray)+u(1,:)/amp_lvl+1i*(imag(inputArray)+u(2,:));
end
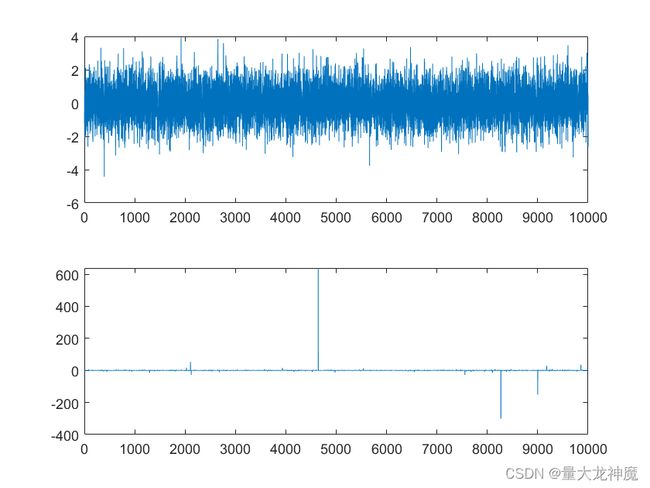
end

仿真如下：基带部分采用10000点的白噪声，设定10dB混合信噪比，，结果如下图所示：

部分参考文献

李旭涛,朱光喜,王首勇,曹汉强.Alpha稳定分布的参数表征及仿真[J].信号处理,2007(06):814-817