数据结构——非线性结构 之 二叉树,详细解析
要认识二叉树,首先要先了解树,二叉树是树的一种特殊的结构。
目录
一、树
1.1树的概念和结构
1.2树的相关专业名词
1.3树和非树
二、二叉树
2.1二叉树的概念的结构
三、二叉树的功能实现
3.1二叉树节点的设计
3.2创建二叉树的新节点
3.3二叉树链式结构的遍历
3.3.1二叉树前序遍历的实现
3.3.1二叉树中序遍历的实现
3.3.1二叉树后序遍历的实现
3.4求二叉树的数据个数(节点个数)的实现
3.5求二叉树的叶子节点个数的实现
3.6销毁二叉树申请的空间的实现
四、二叉树的层序遍历(用的多)
五、总代码
六、代码运行实例
一、树
1.1树的概念和结构
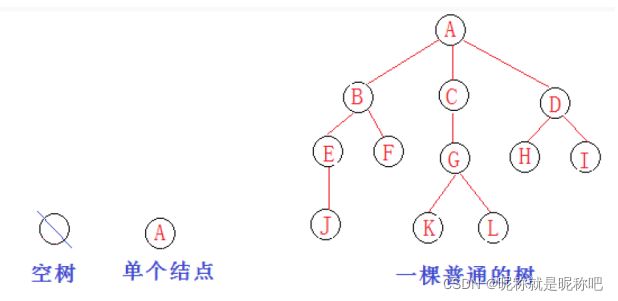
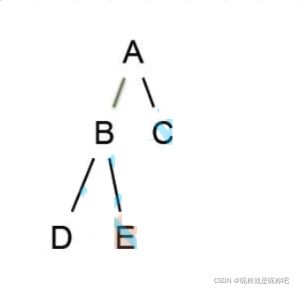
树是一种非线性的数据结构,它是由n(n>=0)个有限节点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。结构如下图所示。
1、空树也是一种树,就是没有节点,可以理解为本来有一棵树,结果被连根挖走了,原来这里的树,就变成了空树。(了解即可)
2、一个节点也能称为树,可以想象成 只有根的树,此时节点A就叫做根节点。
3、一颗普通的树:节点A可以叫做节点B、C、D的根节点,节点B可以叫做节点E、F的根节点,节点E可以叫做节点J的根节点,其他类似;节点A作为 根节点不同于其他根节点,它的上面没有节点,为了区分,我叫做节点A叫做 主根节点。(但是实际上是没有主根节点这个的概念的,只是为了方便理解)
1.2树的相关专业名词
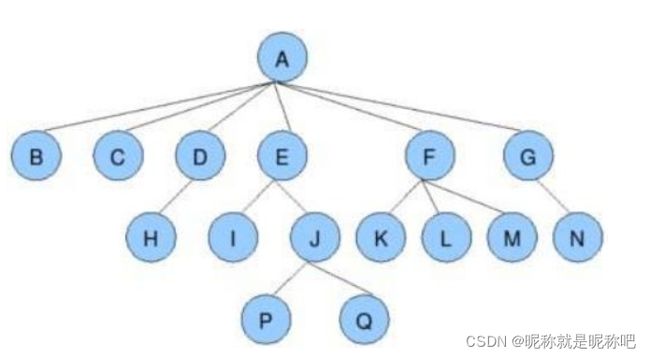
1、树的节点:如上图一棵树,由有限个节点组成,A、B、C ...... Q都叫做树的节点,后面我们称为节点A、节点B ...... 。
2、节点的子树:由某个节点 往下直接相连的节点 叫做 某个节点的子树,如节点A的子树是 节点B、C、D、E、F、G;节点D的子树是 节点H;节点E的子树是 节点I、J;节点J的子树是 节点P、Q;其他类似。
3、节点的度:一个节点含有的 子树的个数 称为该节点的度,如节点A的度是6,因为节点A有6个子树;节点B的度是0,因为节点B没有子树;节点D的度是1,因为节点D有1个子树;其他类似。
4、叶节点(也叫终端节点):度为0的节点称为叶节点;如节点B、C、H、I、P、Q、K、L、M、N都是叶节点(终端节点)。
5、分支节点(也叫非终端节点):度不为0的节点;除了叶节点,其他的都可以叫分支节点。
6、父节点(也叫双亲节点):若一个节点含有子节点,则这个节点称为其子节点的父节点; 如节点A是节点B的父节点。
7、子节点(也叫孩子节点):一个节点含有的子树的根节点称为该节点的子节点; 如节点B是节点A的孩子节点。
8、兄弟节点:具有相同父节点的节点互称为兄弟节点;如节点B、C、D、E、F、G互称为兄弟节点。
9、树的度:一棵树中 ,最大的某个节点的度称为树的度;如上图的树,树的度为6。
10、节点的层次:从主根节点开始定义为第1层,后面以此类推。
11、树的高度(也叫树的深度):树的最大层次;如上图,树的高度为4。
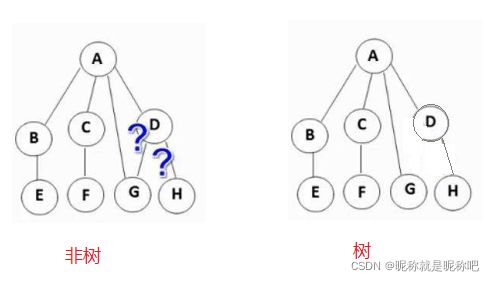
1.3树和非树
树:1、子树是不相交的
2、除了主根节点外,每个节点有且仅有一个父节点
3、一颗N个节点的树有N-1条边
二、二叉树
2.1二叉树的概念的结构
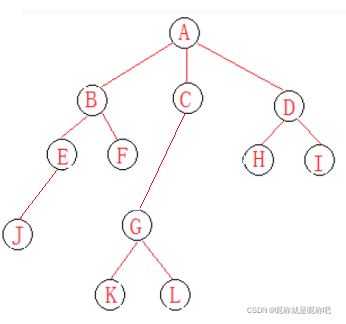
一棵二叉树是节点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成,即二叉树 就是 树的每个节点最多只有两个子树 的树。
二叉树的特点:
1、每个节点最多有两个子树,即二叉树不存在度大于2的节点。
2、二叉树的子树有左右之分,其子树的次序不能颠倒,即在左边的就是左子树,右边的就是右子树,不能改变。
结构图如下:
三、二叉树的功能实现
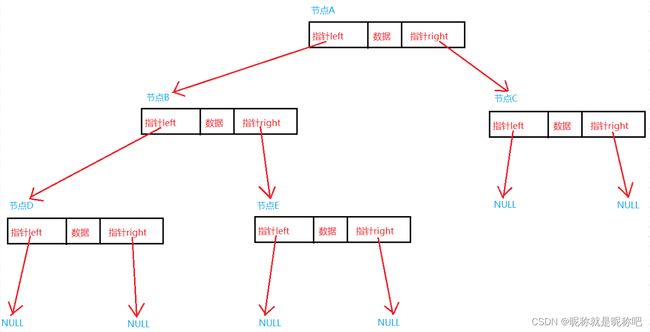
二叉树的存储方式有顺序存储和链式存储,用的多的是链式存储,我们这里讲链式存储。二叉树的链式存储结构是指 用链表来表示一棵二叉树,只不过是非线性链表,即用链来指示元素的逻辑关系。 通常的方法是链表中每个节点由三个域组成,数据域和左右指针域,左右指针分别指向该节点左子树和右子树。
3.1二叉树节点的设计
二叉树储存数据的方式是链式存储的话,即用链表。那么二叉树的节点还是由结构体表示:一个数据,一个指向 这个节点左子树的 指针left,一个指向 这个节点右子树的 指针right。
typedef char BTDataType;//类型重名名
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;//节点里的指针left指向这个节点的左子树
struct BinaryTreeNode* right;//节点里的指针right指向这个节点的右子树
BTDataType data;//这个节点存放的数据
}BTNode;3.2创建二叉树的新节点
//创建新节点
BTNode* BinaryTreeNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));//动态开辟内存空间,大小是一个结构体类型BTnode
if (newnode == NULL)
{
perror("the mistake");
}
newnode->data = x;//将想存放的数据放入节点里
newnode->left = NULL;//创建的新节点里的指针left和right要先置为NULL,方便后面的修改
newnode->right = NULL;//也是因为当这个节点作为根的时候,其左子树和右子树都为NULL
return newnode; //用返回值返回创建的新节点,这样形参就不用创建二级指针了
}以上面的二叉树为例子: 因为每个节点都有指向这个节点左子树和右子树的指针left和right,如果这个节点没有左子树和右子树,那么这个节点的指针left和right则指向空指针(注意这个节点的度就为0,因为实际上它是没有子树的),和单链表链表一样,最后节点里的指针则指向空指针。
3.3二叉树链式结构的遍历
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个节点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础,遍历的思想是递归。
前序/中序/后序的递归结构遍历:是根据访问节点操作发生位置命名
1. NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根节点的操作发生在遍历其左右子树之前。
2. LNR:中序遍历(Inorder Traversal)——访问根节点的操作发生在遍历其左右子树之中。
3. LRN:后序遍历(Postorder Traversal)——访问根节点的操作发生在遍历其左右子树之后。
由于被访问的节点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又
可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
3.3.1二叉树前序遍历的实现
//前序遍历( 根 左子树 右子树 )
void PrevOrder(BTNode* root)//指向根的指针进入
{
if (root == NULL) //两种情况:1、二叉树无节点,直接打印NULL,并结束函数
//2、当递归的作为 根节点 的 左子树 或者 根节点 的 右子树 为空指针NULL的时候,
//这个递归结束,返回上一个递归
{
printf("NULL ");
return;//结束函数
}
printf("%c ", root->data);//打印该节点的存放的数据
PrevOrder(root->left);//这个节点的左子树作为根再进入
PrevOrder(root->right);//这个节点的右子树作为根再进入
}解释请看注解和图,非常详细。
3.3.1二叉树中序遍历的实现
//中序遍历( 左子树 根 右子树 )
void InOrder(BTNode* root)//第一个根节点
{
if (root == NULL)//两种情况:1、二叉树无节点,直接打印NULL,并结束函数
//2、当递归的作为 根节点 的 左子树 或者 根节点 的 右子树 为空指针NULL的时候,
//这个递归结束,返回上一个递归
{
printf("NULL ");
return;//结束函数
}
InOrder(root->left);//这个节点的左子树作为根再进入
printf("%c ", root->data);//打印该节点的存放的数据
InOrder(root->right);//这个节点的右子树作为根再进入
}解释请看注解和图,非常详细。
3.3.1二叉树后序遍历的实现 
//后序遍历( 左子树 右子树 根 )
void PostOrder(BTNode* root)//第一个根节点
{
if (root == NULL)//两种情况:1、二叉树无节点,直接打印NULL,并结束函数
//2、当递归的作为 根节点 的 左子树 或者 根节点 的 右子树 为空指针NULL的时候,
//这个递归结束,返回上一个递归
{
printf("NULL ");
return;//结束函数
}
PostOrder(root->left);//这个节点的左子树作为根再进入
PostOrder(root->right);//这个节点的右子树作为根再进入
printf("%c ", root->data);//打印该节点的存放的数据
}解释请看注解和图,非常详细。
3.4求二叉树的数据个数(节点个数)的实现
//求二叉树的数据个数,二叉树每个节点只存放一个数据,
//所以也可以说求二叉树的节点个数(用的遍历后序的思维)
int TreeSize(BTNode* root)
{
//三目操作符:exp1?exp2:exp3
//如果 表达式exp1 为真,则 整个表达式 的结果为 表达式exp2;如果为假,则 整个表达式 的结果为 表达式exp3
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}解释请看注解,非常详细。
3.5求二叉树的叶子节点个数的实现
//求二叉树叶子节点(度为0的节点)的个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)//二叉树里没有节点
return 0;
if (root->left == NULL && root->right == NULL)//二叉树里只有一个节点,那么这个节点就是叶子节点
return 1;
//进入递归,找左子树的叶子节点+找右子树的叶子节点
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}解释请看注解,非常详细。
3.6销毁二叉树申请的空间的实现
void DestroyTree(BTNode* root)
{
if (root == NULL)
{
return;
}
DestroyTree(root->left);//将当前节点的左子树作为根节点递归
DestroyTree(root->right);//将当前节点的左子树作为根节点递归
free(root);//释放点节点的空间
//root = NULL;//这里将root置为空指针没有意义,因为这个函数的参数是 值传递 ,
//是将指针root存放的地址拷贝了一份给函数内部创建的指针root,我们是想将函数外的指针root置为空指针,
//这里因为是值传递,所以只是将函数内部创建的临时指针root置为空,值传递形参的改变不影响实参,
//所以函数外部的指针root依旧存放的是动态开辟的 大小是结构体类型 的空间的地址,并没有变为空指针NULL。
//这里如果非要改变,那么就用二级指针,或者不用管,因为整个程序结束后,申请的所有空间都会销毁(返还)
}解释请看注解,非常详细。
四、二叉树的层序遍历(用的多)
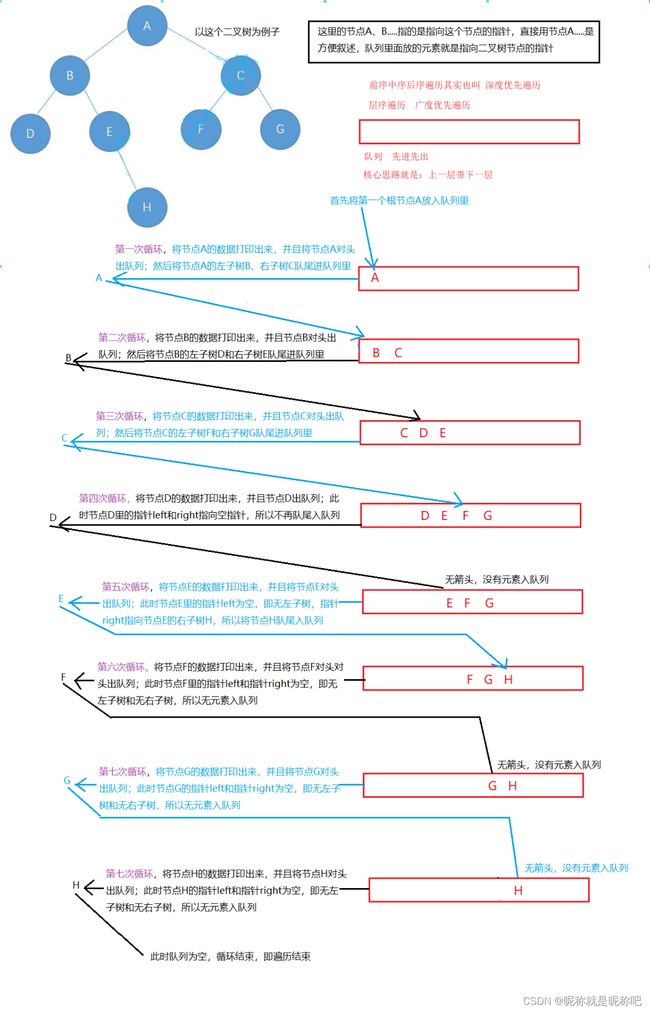
二叉树的层序遍历,用到了线性表的队列,队列是先进先出,用队列的实现二叉树的核心思路是:上一层带下一层。解释请看代码的注解和图片,非常详细。
//层序遍历二叉树的节点的数据(需要用到队列)
void LevelOrder(BTNode* root)//传指向二叉树根节点的指针
{
// 核心思路:上一层出的时候带下一层节点进;
//队列里的元素是指向二叉树节点的指针
Queue q;//创建一个结构体类型Queue的变量,这个结构体里放的是
//一个指向第一个节点的指针head和一个指向尾节点的指针tail
QueueInit(&q);//初始化这个结构体,地址传递,可以改变实参
if (root)//判断二叉树是否有节点
QueuePush(&q, root);//将 指向二叉树根节点的指针 作为元素 队尾入队列里
//此时队列里 只有 指向二叉树根节点的指针这一个元素
while (!QueueEmpty(&q))//队列里非空,就继续;队列空,就跳出循环
{
BTNode* front = QueueFront(&q);//将对头的元素由临时变量存放
QueuePop(&q);//对头出 队列对头的元素
printf("%c ", front->data);//打印 对头的元素 里存放的元素
//即打印的二叉树节点里存放的数据
if (front->left)//该节点的左子树不为空指针,则将左子树队尾入队列里
{
QueuePush(&q, front->left);
}
if (front->right)//该节点的右子树不为空指针,则将右子树队尾入队列里
{
QueuePush(&q, front->right);
}
}
printf("\n");
QueueDestory(&q);//销毁队列的空间
}五、总代码
这是总代码的地址,有需要的可以自取:放代码: 代码 - Gitee.com
六、代码运行实例
前序遍历的顺序:A B D NULL NULL E NULL NULL C NULL NULL
中序遍历的顺序:NULL D NULL B NULL E NULL A NULL C NULL
后序遍历的顺序:NULL NULL D NULL NULL E B NULL NULL C A
节点A作为第一个根节点的二叉树元素个数:5
节点B作为第一个根节点的二叉树元素个数:3
节点A作为第一个根节点的二叉树叶子节点的个数:3
节点B作为第一个根节点的二叉树叶子节点的个数:2