一本通OJ 1810 登山 题解
题目链接
题目大意
从 ( 0 , 0 ) (0,0) (0,0) 走到 ( n , n ) (n,n) (n,n) ,不能超过直线 y = x y=x y=x,并且图上有 m m m 个点不能走,问你有几种方案
解题思路
很明显这题与卡特兰数有关,但是不同点在于这题中存在点不能走
考虑容斥,我们要求出总方案数和不合法方案数相减
总方案数即是卡特兰数
假设 f i f_i fi 是从 ( 0 , 0 ) (0,0) (0,0) 走到第 i i i 个不能走的点 ( x i , y i ) (x_i,y_i) (xi,yi) 且不经过之前任何一个不能走的点的方案数
这样就能保证不会重复统计
考虑 f i f_i fi 如何递推:
再次考虑容斥, f i f_i fi 等于从 ( 0 , 0 ) (0,0) (0,0) 走到 ( x i , y i ) (x_i,y_i) (xi,yi) 的方案数减从 ( x i − 1 , y i − 1 ) (x_{i-1},y_{i-1}) (xi−1,yi−1) 走到 ( x i , y i ) (x_i,y_i) (xi,yi) 的方案数乘 f i − 1 f_{i-1} fi−1
那么现在需要解决的是,如何求从 ( x a , y a ) (x_a,y_a) (xa,ya) 走到 ( x b , y b ) (x_b,y_b) (xb,yb) 的方案数
具体的,我们假定从 ( 3 , 0 ) (3,0) (3,0) 走到 ( 6 , 5 ) (6,5) (6,5)

接下来以这个例子来解释做法,再次考虑容斥原理
如果不考虑不超过 y = x y=x y=x,那么从 ( 3 , 0 ) (3,0) (3,0) 走到 ( 6 , 5 ) (6,5) (6,5) 总共有 C 6 − 3 + 5 − 0 6 − 3 C_{6-3+5-0}^{6-3} C6−3+5−06−3 种
不超过 y = x y=x y=x 等价于不经过 y = x + 1 y=x+1 y=x+1,我们将点 ( 6 , 5 ) (6,5) (6,5) 对称过去得到点 ( 4 , 7 ) (4,7) (4,7)
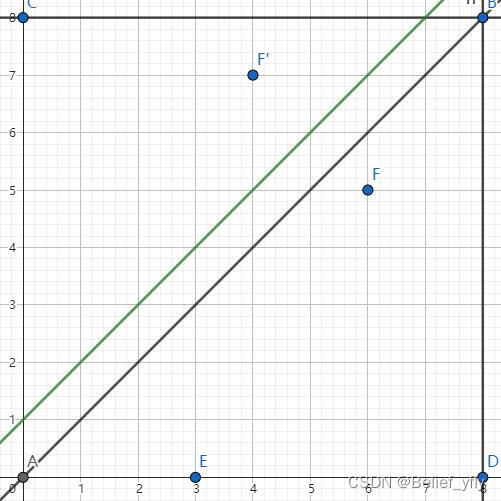
从 ( 3 , 0 ) (3,0) (3,0) 走到 ( 4 , 7 ) (4,7) (4,7) 的方案数与从 ( 3 , 0 ) (3,0) (3,0) 走到 ( 6 , 5 ) (6,5) (6,5) 的不合法的方案是相等
解释如图,从 ( 3 , 0 ) (3,0) (3,0) 走到 ( 4 , 7 ) (4,7) (4,7) 的路线超出 y = x + 1 y=x+1 y=x+1 的部分对称回去即可走到 ( 6 , 5 ) (6,5) (6,5)

从 ( 3 , 0 ) (3,0) (3,0) 走到 ( 4 , 7 ) (4,7) (4,7) 总共有 C 4 − 3 + 7 − 0 4 − 3 C_{4-3+7-0}^{4-3} C4−3+7−04−3 种
因此从 ( 3 , 0 ) (3,0) (3,0) 走到 ( 6 , 5 ) (6,5) (6,5) 的合法的方案即为 C 6 − 3 + 5 − 0 6 − 3 − C 4 − 3 + 7 − 0 4 − 3 C_{6-3+5-0}^{6-3}-C_{4-3+7-0}^{4-3} C6−3+5−06−3−C4−3+7−04−3
( x b , y b ) (x_b,y_b) (xb,yb) 关于 y = x + 1 y=x+1 y=x+1 对称即为 ( y b − 1 , x b + 1 ) (y_b-1,x_b+1) (yb−1,xb+1),不合法方案数 C y b − 1 − x a + x b + 1 − y a y b − 1 − x a = C x b − x a + y b − y a y b − x a − 1 C_{y_b-1-x_a+x_b+1-y_a}^{y_b-1-x_a}=C_{x_b-x_a+y_b-y_a}^{y_b-x_a-1} Cyb−1−xa+xb+1−yayb−1−xa=Cxb−xa+yb−yayb−xa−1
由此可以推导得出,从 ( x a , y a ) (x_a,y_a) (xa,ya) 走到 ( x b , y b ) (x_b,y_b) (xb,yb) 的方案数为 C x b − x a + y b − y a x b − x a − C x b − x a + y b − y a y b − x a − 1 C_{x_b-x_a+y_b-y_a}^{x_b-x_a}-C_{x_b-x_a+y_b-y_a}^{y_b-x_a-1} Cxb−xa+yb−yaxb−xa−Cxb−xa+yb−yayb−xa−1
Q:如果出现 y b − 1 < x a y_b-1
A:可以发现这种情况不存在不合法方案,所以方案数即为 C x b − x a + y b − y a x b − x a C_{x_b-x_a+y_b-y_a}^{x_b-x_a} Cxb−xa+yb−yaxb−xa
最后答案就是从 ( 0 , 0 ) (0,0) (0,0) 走到 ( n , n ) (n,n) (n,n) 的方案数减从 ( x m , y m ) (x_m,y_m) (xm,ym) 走到 ( n , n ) (n,n) (n,n) 的方案数乘 f m f_m fm
因此也可以把 ( n , n ) (n,n) (n,n) 变成第 m + 1 m+1 m+1 个点进行同样操作
code
#include