【数据结构】树状数组和线段树

树状数组和线段树

下文为自己的题解总结，参考其他题解写成，取其精华，做以笔记，如有描述不清楚或者错误麻烦指正，不胜感激，不喜勿喷！

树状数组

• 需求：

  • 能够快速计算区间和
  • 保证在修改了数组的值之后，对相关数据结构内容修改的操作数尽量少

  —>同时包含多个节点信息—>树状数组或二叉索引树（Binary Indexed Tree）

• 用途

  • 能够解决数据压缩里的累积频率的计算问题，现多用于高效计算数列的前缀和、区间和。
  • 求逆序对

• 特点

  • 底部确定，顶部无穷大
  • 最外面的结点是2的n次方
  • 奇数的结点一定是叶子结点
  • 数组一定要从1开始

  

• 复杂度

  • 它可以以 O(logn) 的时间得到任意前缀和，并同时支持在 O(logn) 时间内支持动态单点值的修改
  • 空间复杂度 O(n)

• 定义：每一列的顶端节点C数组为树状数组，C[i]代表子树的叶子节点的权值之和

  • C[1]=A[1];
  • C[2]=A[1]+A[2];
  • C[3]=A[3];
  • C[4]=A[1]+A[2]+A[3]+A[4];
  • C[5]=A[5];
  • C[6]=A[5]+A[6];
  • C[7]=A[7];
  • C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

  

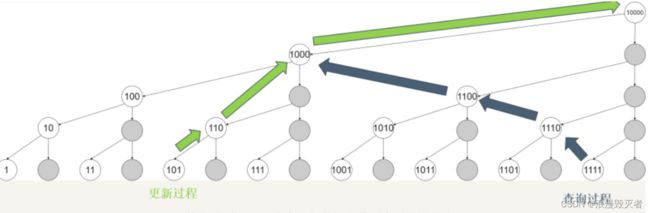
• 更新过程：当A5发生改变时，节点的修改过程

  • 当A5发生改变时，会导致C5—>C6—>C8发送变化，变化的值为A5新值-A5旧值

  • 101—>110—>1000—>10000

  • 通过二进制快速获取修改的节点

    • 101加最低位1—>110
    • 110加最低位10—>1000
    • 1000加最低位1000—>10000
    • 因此只需要计算出当前节点下标二进制表示的最低位1的所表示的值(最小元lowbit)，就可以计算出下一个要修改的节点

    

• 查询过程：查询下标15的前缀和，从A[0]到A[15]的所有值之和

  • 8节点包含了1~8，12节点包含了9~12，14节点包含了13~14，15节点包含了15

  • 1111—>1110—>1100—>1000

  • 通过二进制快速获取需要的节点

    • 1111减最低位1—>1110
    • 1110减最低位10—>1100
    • 1100减最低位100—>1000
    • 1000减最低位1000—>0 退出循环

• 实现原理

  • 获得二进制：取数组下标二进制非0最低位所表示的值

    int lowbit(int x) {
        return x & -x;
    }
    

    • x & -x：x 与 该数的补码[一个数的负数=这个数的补码=取反+1]相与
    • 解释：反码与原码相反，将反码+1后得到的补码由于进位那么最低位的1和原码最低位的1一定是同一个位置，因此通过x & -x可以取出最低位的1

  • 单点更新：不断反复，直到当前需要修改的节点下标越界即可

    void add(int x, int val) {
         for (int i = x; i <= n; i += lowbit(i)) tr[i] += val ;
    }
    

  • 区间查询：将从A[0]到A[i]的所有值求和

    int query(int x){
        int sum = 0;
        for(int i=x;i>0;i-=lowbit(i)){
            sum += tr[i];
        }
        return sum;
    }
    

• 完整代码【求前缀和】

  int n;
  int[] tr;
  int lowbit(int x) {
      return x & -x;
  }
  // 在树状数组 x 位置中增加值 val
  void add(int x, int val) {
       for (int i = x; i <= n; i += lowbit(i)) tr[i] += val ;
  }
  // 查询前缀和的方法
  int query(int x){
      int sum = 0;
      for(int i=x;i>0;i-=lowbit(i)){
          sum += tr[i];
      }
      return sum;
  }
  

• 完整代码【求逆序对】

  • 对于nums[i]，其左边比它大的nums[j]的个数，即为以nums[i]为右端点的逆序对的数量
  • tr[i]代表当前已经遍历到的数组数值小于等于i的总数量

  class Solution {
      int n;
      int[] tr;
      int lowbit(int x) {
          return x & -x;
      }
      void add(int x) {
          for (int i = x; i <= n; i += lowbit(i)) tr[i]++;
      }
      int query(int x) {
          int ans = 0;
          for (int i = x; i > 0; i -= lowbit(i)) ans += tr[i];
          return ans;
      }
      public boolean isIdealPermutation(int[] nums) {
          n = nums.length;
          tr = new int[n + 10];
          add(nums[0] + 1);// 更新tr数组下标0-nums[0]+1 使其数量+1
          int a = 0;
          for (int i = 1; i < n; i++) {
              a += query(n) - query(nums[i] + 1);
              // query(n)为当前加入的数的总数，即等于i
              // query(nums[i] + 1) 为nums[0,i-1]小于等于nums[i] + 1的数量
              // 相减即为以nums[i]为右端点的逆序对的数量【全局倒置】
              add(nums[i] + 1);
          }
          return a;
      }
  }
  

线段树

• 线段树是什么？

  线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

  对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。

  使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

  • 线段树能够对编号连续的一些点进行修改或者统计操作，修改和统计的复杂度都是$O(logn)$
  • 线段树的原理，将[1,n]分解成若干特定的子区间(数量不超过4n),然后，将每个区间[L,R]都分解为少量特定的子区间，通过对这些少量子区间的修改或者统计，来实现快速对[L,R]的修改或者统计。

• 用途

  它能够高效的处理区间修改查询等问题，但是用线段树统计的东西，必须符合区间加法，否则，不可能通过分成的子区间来得到[L,R]的统计结果。

  • 符合区间加法的例子：

    数字之和——总数字之和 = 左区间数字之和 + 右区间数字之和

    最大公因数(GCD)——总GCD = gcd( 左区间GCD , 右区间GCD );

    最大值——总最大值=max(左区间最大值，右区间最大值)

  • 不符合区间加法的例子：

    众数——只知道左右区间的众数，没法求总区间的众数

    01序列的最长连续零——只知道左右区间的最长连续零，没法知道总的最长连续零

• 原理

  注：由于线段树的每个节点代表一个区间，以下叙述中不区分节点和区间，只是根据语境需要，选择合适的词

  线段树本质上是维护下标为0,2,…,n-1的n个按顺序排列的数的信息，所以，其实是“点树”，维护n个点的信息，至于每个点的数据的含义可以有很多，在对线段操作的线段树中，每个点代表一条线段，在用线段树维护数列信息的时候，每个点代表一个数，但本质上都是每个点代表一个数。以下，在讨论线段树的时候，区间[L,R]指的是下标从L到R的这(R-L+1)个数，而不是指一条连续的线段。只是有时候这些数代表实际上一条线段的统计结果而已。

  • 建树：

    存储结构：数组/结构体

    线段树用数组来模拟树形结构，对于某一个节点下标为$m$，其左子节点的下标为$2m=(m<<1)$，右子节点的下标为$2m+1=(m<<1+1)$

    线段树的每个节点代表一个区间，区间[L,R]指的是下标从L到R的这(R-L+1)个数

    • 子区间的划分：每个区间[L,R]划分为左子区间$[L,M]$，右子区间$[M+1,R]$，其中$M=(L+R)/2$

      

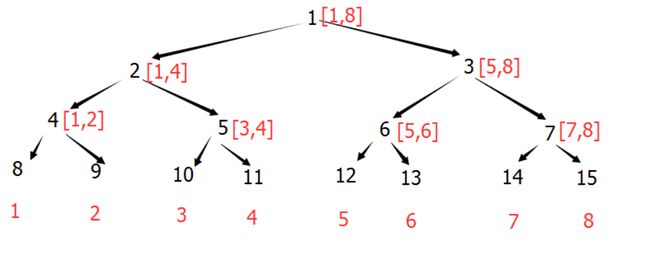
      • 原数组下标：需要维护统计信息（比如区间求和）的数组的下标，这里都默认下标从1开始（一般用A数组表示）
      • 线段树下标：加入线段树中某个位置的下标，比如，原数组中的第一个数，一般会加入到线段树中的第二个位置，为什么要这么做，后面会讲。
      • 存储下标：是指该元素所在的叶节点的编号，即实际存储的位置。

    • 【在上面的图片中，红色为原数组下标，黑色为存储下标】

    • 线段树所需要的空间：原数组大小的4倍

      实际上足够的空间 = （n向上扩充到最近的2的某个次方）的两倍。

  • 点修改

    修改某一个元素的值，需要将线段树中每层包含该元素的区间进行更新，修改次数的最大值为层数$\lfloor log_2(n-1)\rfloor + 1 $，复杂度为$O(logn)$

  • 区间查询

    当$n\ge 3$，一个$[1,n]$的线段树可以将$[1,n]$的任意子区间$[L,R]$分解为不超过$2\lfloor lo{g}_2(n-1)\rfloor$ 个子区间。

    因此，在查询区间$[L,R]$的统计值（题目要求的值）时，只需要访问不超过$2\lfloor lo{g}_2(n-1)\rfloor$个节点，复杂度为$O(logn)$

  • 区间修改+懒标记

    考虑对某一个区间加上一个数，我们可以从根节点不断向下查找，当发现我们要修改的区间覆盖了当前节点时，我们就把这个区间给修改，并打上懒标记（由于懒标记存在，我们就不必再修改他的儿子节点，在查询到儿子时再进行修改），否则下传懒标记，继续向下找

• 实现模板（递归+结构体）

  题目：
  10000个正整数，编号1到10000，用A[1],A[2],A[10000]表示。

  编号从L到R的所有数之和为多少？ 其中1<= L <= R <= 10000.

  对于某个数增加C后，编号从L到R的所有数之和为多少？

  • 关于线段树设计的几种操作：

    • void build(int u, int l, int r)：含义为从编号为 u 的节点开始，构造范围为 [l,r] 的树节点；
    • void update(int u, int index,int val)：含义为从编号为 u 的节点开始搜寻，在 index位置增加 val，更具一般性；
    • int query(int u, int l, int r)：含义为从编号为 u的节点开始，查询 $[l,r]$区间和为多少。
    • void updateAll(int u, int l, int r, int val)：涉及区间修改的操作应该为，代表在 $[l,r]$范围增加 val；
    • void pushdown(int u)：实现将懒标记下推（父节点往下传递「更新」的操作）
    • f(u)：根据懒标记，修改当前节点
    • void pushUp(int u)：向上更新

  class Node {
      int l, r;
      int sum;// 和 题目所要求的值
      int lazy;// 延迟修改的值
  }
  
  class SegmentTree {
      private Node[] tr;// 线段树
      private int[] nums;// 原数组
  
      public SegmentTree(int[] nums) {
          int n = nums.length;
          this.nums = nums;
          tr = new Node[n << 2];
          for (int i = 0; i < tr.length; ++i) {
              tr[i] = new Node();
          }
          build(1, 1, n);// 建树
      }
  
      private void build(int u, int l, int r) {// l,r表示当前区间 u表示当前节点编号（1,n）
          tr[u].l = l;
          tr[u].r = r;
          if (l == r) {// 若到达叶子节点
              tr[u].sum = nums[l - 1];// 存储值
              return;
          }
          // 左右递归
          int mid = (l + r) >> 1;
          build(u << 1, l, mid);
          build(u << 1 | 1, mid + 1, r);
          pushup(u);// 更新信息
      }
  	// 区间查询
      public int query(int u, int l, int r) {
           if (tr[u].l >= l && tr[u].r <= r) {         
               // 在区间内，直接返回 
              return tr[u].sum;
          }
          pushdown(u);// 懒标记下推
          int res = 0;
          int mid = (tr[u].l + tr[u].r) >> 1;      
          if (l <= mid) {
              res += query(u << 1, l, mid);
          }
          if (r > mid) {
              res += query(u << 1 | 1, mid + 1, r);
          }
          return res;
      }
  	
  
      // 单点修改:nums[index] += val
      public void update(int u, int index,int val){// u表示当前节点编号,index代表修改点的位置
          if(tr[u].l == tr[u].r){//到叶节点，修改 
              tr[u].sum += val;
              return;
          }
          int m = (tr[u].l + tr[u].r) >> 1;
          //根据条件判断往左子树调用还是往右 
          if(index <= m) {
              update(u << 1, index, C);
          }
          else{
              update(u << 1 | 1, index, C);
          }       
          pushup(u);//子节点更新了，所以本节点也需要更新信息 
      }
      // 区间修改:nums[l, r] += val
      public void updateAll(int u, int l, int r, int val) {
          if (tr[u].l >= l && tr[u].r <= r) {
              f(u, val);
              return;
          }
          // 在回溯之前向下传递修改标记
          pushdown(u);
          int mid = (tr[u].l + tr[u].r) >> 1;
          if (l <= mid) {
              updateAll(u << 1, l, r, val);
          }
          if (r > mid) {
              updateAll(u << 1 | 1, l, r, val);
          }
          pushup(u);// 更新本节点信息
      }
      // pushUp函数更新节点信息, 本题是求和
      private void pushup(int u) {
          tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
      }
      // 懒加载
      private void pushdown(int u) {
      	if (tr[u].lazy != 0) {// 如果懒标记不为0，就将其下传，修改左右儿子维护的值
              f(u << 1, tr[u].lazy);
              f(u << 1 | 1, tr[u].lazy);
              tr[u].lazy = 0;// 向下传之后将该节点的懒标记清0
      	}
      }
      // 父节点修改时，维护子节点的更新
      private void f(int u, int add){
          tr[u].s += add * (tr[u].r - tr[u].l + 1);
          tr[u].lazy += add;
      }
  
  }
  
  

相关题目【都可】

区域和检索 - 数组可修改【LC307】

给你一个数组 nums ，请你完成两类查询。

1. 其中一类查询要求 更新 数组 nums 下标对应的值
2. 另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 ，其中 left <= right

实现 NumArray 类：

• NumArray(int[] nums) 用整数数组 nums 初始化对象
• void update(int index, int val) 将 nums[index] 的值 更新 为 val
• int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 （即，nums[left] + nums[left + 1], ..., nums[right]）

线段树

• 关于线段树设计的几种操作：

  • void build(int u, int l, int r)：含义为从编号为 u 的节点开始，构造范围为 [l,r] 的树节点；
  • void update(int u, int x, int v)：含义为从编号为 u 的节点开始，在 x 位置增加 v，更具一般性；
  • int query(int u, int l, int r)：含义为从编号为 uu的节点开始，查询 $[l,r]$区间和为多少。

• 实现

  class NumArray {
      private SegmentTree segmentTree;
      int n;
      int[] nums;
      public NumArray(int[] nums) {
          this.n = nums.length;
          this.nums = nums;
          segmentTree = new SegmentTree(nums);
      }
      
      public void update(int index, int val) {
  
          segmentTree.update(1，index + 1, val - nums[index]);
          nums[index] = val;
      }
      
      public int sumRange(int left, int right) {
          return segmentTree.query(1, left + 1, right + 1);
      }
  }
  class Node {
      int l, r;
      int sum;// 和 题目所要求的值
  
  }
  
  class SegmentTree {
      private Node[] tr;// 线段树
      private int[] nums;// 原数组
  
      public SegmentTree(int[] nums) {
          int n = nums.length;
          this.nums = nums;
          tr = new Node[n << 2];
          for (int i = 0; i < tr.length; ++i) {
              tr[i] = new Node();
          }
          build(1, 1, n);// 建树
      }
  
      private void build(int u, int l, int r) {// l,r表示当前区间 u表示当前节点编号（1,n）
          tr[u].l = l;
          tr[u].r = r;
          if (l == r) {// 若到达叶子节点
              tr[u].sum = nums[l - 1];// 存储值
              return;
          }
          // 左右递归
          int mid = (l + r) >> 1;
          build(u << 1, l, mid);
          build(u << 1 | 1, mid + 1, r);
          pushUp(u);// 更新信息
      }
  	
  	// pushUp函数更新节点信息, 本题是求和
      private void pushUp(int u) {
          tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
      }
      // 单点修改:nums[index] += val
      public void update(int u, int index,int val){// u表示当前节点编号,index代表修改点的位置
          if(tr[u].l == tr[u].r){//到叶节点，修改 
              tr[u].sum += val;
              return;
          }
          int m = (tr[u].l + tr[u].r) >> 1;
          //根据条件判断往左子树调用还是往右 
          if(index <= m) {
              update(u << 1, index, C);
          }
          else{
              update(u << 1 | 1, index, C);
          }       
          pushUp(u);//子节点更新了，所以本节点也需要更新信息 
      }
      // 区间查询
      public int query(int u, int l, int r) {
           if (tr[u].l >= l && tr[u].r <= r) {
               // 在区间内，直接返回 
              return tr[u].sum;
          }
          int res = 0;
          int mid = (tr[u].l + tr[u].r) >> 1;
          
          if (l <= mid) {
              res += query(u << 1, l, r);
          }
          if (r > mid) {
              res += query(u << 1 | 1, l, r);
          }
          return res;
      }
  }
  
  
  /**
   * Your NumArray object will be instantiated and called as such:
   * NumArray obj = new NumArray(nums);
   * obj.update(index,val);
   * int param_2 = obj.sumRange(left,right);
   */
  

  • 复杂度
    • 时间复杂度：初始化时间复杂度为$O(n)$，查询复杂度为$O(logn)$
    • 空间复杂度：$O(n)$

树状数组【推荐】

• 思路

  本题只涉及「单点修改」和「区间求和」，属于「树状数组」的经典应用。

  树状数组涉及的操作有两个，复杂度均为 $O(logn)$：

  • void add(int x, int u)：含义为在 x 的位置增加 u（注意位置下标从 1开始）；
  • int query(int x)：含义为查询从 $[1,x]$区间的和为多少（配合容斥原理，可实现任意区间查询）

  class NumArray {
      int[] tr;
      int lowbit(int x) {
          return x & -x;
      }
      void add(int x, int u) {
          for (int i = x; i <= n; i += lowbit(i)) tr[i] += u;
      }
      int query(int x) {
          int ans = 0;
          for (int i = x; i > 0; i -= lowbit(i)) ans += tr[i];
          return ans;
      }
  
      int[] nums;
      int n;
      public NumArray(int[] _nums) {
          nums = _nums;
          n = nums.length;
          tr = new int[n + 10];
          for (int i = 0; i < n; i++) add(i + 1, nums[i]);
      }
      public void update(int index, int val) {
          add(index + 1, val - nums[index]);
          nums[index] = val;
      }
      public int sumRange(int left, int right) {
          return query(right + 1) - query(left);
      }
  }
  
  作者：宫水三叶
  链接：https://leetcode.cn/problems/range-sum-query-mutable/solutions/1393108/by-ac_oier-zmbn/
  来源：力扣（LeetCode）
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
  

  • 复杂度
    • 时间复杂度：初始化时间复杂度为$O(n)$，查询复杂度为$O(logn)$
    • 空间复杂度：$O(n)$

区间和的个数【LC327】

给你一个整数数组 nums 以及两个整数 lower 和 upper 。求数组中，值位于范围 [lower, upper] （包含 lower 和 upper）之内的 区间和的个数 。

区间和 S(i, j) 表示在 nums 中，位置从 i 到 j 的元素之和，包含 i 和 j (i ≤ j)。

线段树相关

*子数组中占绝大多数的元素【LC1157】

线段树

设计一个数据结构，有效地找到给定子数组的 多数元素 。

子数组的 多数元素 是在子数组中出现 threshold 次数或次数以上的元素。

实现 MajorityChecker 类:

• MajorityChecker(int[] arr) 会用给定的数组 arr 对 MajorityChecker 初始化。
• int query(int left, int right, int threshold) 返回子数组中的元素 arr[left...right] 至少出现 threshold 次数，如果不存在这样的元素则返回 -1。

• 思路

  需要求解的问题有两个：找出 可能的 绝对众数和统计这个数出现的次数

  • 由于题目中2 * threshold > right - left + 1，因此可以得出结论：每次查询时不一定存在多数元素，但存在多数元素的话找到的一定是多数元素）

  • 而某个区间的多数元素，符合区间加法，区间$[L,R]$的多数元素一定是区间$[L,M]$和区间$[M+1,R]$的多数元素中的其中一个，因此可以使用线段树的方式解决该问题

  • 需要注意的是，通过线段树查找到的$x$只是可能的多数元素（摩尔投票），是否真的是答案，需要通过二分查找判断：记录每个数字出现的索引，找到 x在数组中第一个大于等于 left的下标 l，以及第一个大于 righ的下标 r。如果 r−l≥threshold，则返回 x，否则返回 −1

  • 摩尔投票可以找到数组中的多数元素

    如果一个数组有大于一半的数相同，那么任意删去两个不同的数字，新数组还是会有相同的性质。

    根据在数组中出现次数将数字划分两类。

    • 第一类，出现次数大于半数的数字，假设为x，也是要找的数字。
    • 第二类，出现次数小于半数的数字，假设为y，出现次数小于半数的数字可能有很多种，因为具体是几不重要，我们可以统一设为y。

    那么，x出现次数 - y出现次数 > 0。 因此，我们统计当前众数x，和x众数出现的次数count，遇到一个y，将count–；如果count=0，说明当前没有数字是众数；如果当前数字等于x，那么将count++。因为众数一定存在，所以最后x即为众数且count>0。

• 实现

  class Node {
      int l, r;
      int x, cnt;
  }
  
  class SegmentTree {
      private Node[] tr;
      private int[] nums;
  
      public SegmentTree(int[] nums) {
          int n = nums.length;
          this.nums = nums;
          tr = new Node[n << 2];
          for (int i = 0; i < tr.length; ++i) {
              tr[i] = new Node();
          }
          build(1, 1, n);
      }
  
      private void build(int u, int l, int r) {
          tr[u].l = l;
          tr[u].r = r;
          if (l == r) {// 若到达叶节点
              tr[u].x = nums[l - 1];// 存储值
              tr[u].cnt = 1;// 存储次数
              return;
          }
          int mid = (l + r) >> 1;
          // 左右递归
          build(u << 1, l, mid);
          build(u << 1 | 1, mid + 1, r);
          pushup(u);
      }
  
      public int[] query(int u, int l, int r) {
          if (tr[u].l >= l && tr[u].r <= r) {// 在区间内，直接返回 
              return new int[] {tr[u].x, tr[u].cnt};
          }
          int mid = (tr[u].l + tr[u].r) >> 1;
          if (r <= mid) {
              return query(u << 1, l, r);// 答案在左子树
          }
          if (l > mid) {
              return query(u << 1 | 1, l, r);// 答案在右子树
          }
          // 答案与左右子树相关
          var left = query(u << 1, l, r);// 左子树的多数元素和次数
          var right = query(u << 1 | 1, l, r);// 右子树的多数元素和次数
          if (left[0] == right[0]) {// 值相等次数相加
              left[1] += right[1];
              return left;
          } else if (left[1] >= right[1]) {// 值不相等，返回次数较大值，次数为较大值次数-较小值次数 （因为如果相等那么表示，一定不存在多数元素）【不减直接返回也可以通过】
              // left[1] -= right[1];
              return left;
          } else {
              return right;
              // right[1] -= left[1];
              // left = right;
          }
      }
  	// 更新节点信息 
      private void pushup(int u) {
          // 将节点信息更新为左右节点的次数最大值
          if (tr[u << 1].x == tr[u << 1 | 1].x) {// 相等 那么次数相加
              tr[u].x = tr[u << 1].x;
              tr[u].cnt = tr[u << 1].cnt + tr[u << 1 | 1].cnt;
          } else if (tr[u << 1].cnt >= tr[u << 1 | 1].cnt) {// 不相等 那么次数相减（摩尔投票）
              tr[u].x = tr[u << 1].x;
              tr[u].cnt = tr[u << 1].cnt - tr[u << 1 | 1].cnt;
          } else {
              tr[u].x = tr[u << 1 | 1].x;
              tr[u].cnt = tr[u << 1 | 1].cnt - tr[u << 1].cnt;
          }
      }
  }
  
  class MajorityChecker {
      private SegmentTree tree;
      private Map<Integer, List<Integer>> d = new HashMap<>();
  
      public MajorityChecker(int[] arr) {
          tree = new SegmentTree(arr);
          for (int i = 0; i < arr.length; ++i) {// 记录每个数出现的下标
              d.computeIfAbsent(arr[i], k -> new ArrayList<>()).add(i);
          }
      }
  
      public int query(int left, int right, int threshold) {
          int x = tree.query(1, left + 1, right + 1)[0];// 候选元素
          // 二分查找
          int l = search(d.get(x), left);// 原数组中下标小于left的x的个数
          int r = search(d.get(x), right + 1);// 原数组中下标小于right + 1的x的个数
          // 相减即为区间[l,r]中x的个数
          return r - l >= threshold ? x : -1;
      }
  
      private int search(List<Integer> arr, int x) {
          // 左闭右开
          int left = 0, right = arr.size();
          while (left < right) {
              int mid = (left + right) >> 1;
              if (arr.get(mid) >= x) {
                  right = mid;
              } else {
                  left = mid + 1;
              }
          }
          return left;
      }
  }
  

  • 复杂度
    • 时间复杂度：初始化时间复杂度为$O(n)$，查询复杂度为$O(logn)$
    • 空间复杂度：$O(n)$

更新数组后处理求和查询【LC2569】

给你两个下标从 0 开始的数组 nums1 和 nums2 ，和一个二维数组 queries 表示一些操作。总共有 3 种类型的操作：

1. 操作类型 1 为 queries[i] = [1, l, r] 。你需要将 nums1 从下标 l 到下标 r 的所有 0 反转成 1 或将 1 反转成 0 。l 和 r 下标都从 0 开始。
2. 操作类型 2 为 queries[i] = [2, p, 0] 。对于 0 <= i < n 中的所有下标，令 nums2[i] = nums2[i] + nums1[i] * p 。
3. 操作类型 3 为 queries[i] = [3, 0, 0] 。求 nums2 中所有元素的和。

请你返回一个数组，包含所有第三种操作类型的答案。

• 思路

  题目要求求出进行操作3时， nums2 中所有元素的和。操作2会更改nums2，每进行一次操作2，和增加$p\ast sum(nums1)$；而操作1会将nums1某个区间的01进行反转。因此我们需要一种数据结构快速计算出计进行反转后nums1中的区间和，该性质满足可加性，因此可以使用线段树。【套板子】

  • 定义线段树的每个节点为 Node，每个节点包含如下属性：

    • l：节点的左端点，下标从 1开始。
    • r：节点的右端点，下标从 1 开始。
    • sum：节点的区间和。
    • lazy：节点的懒标记。

  • 线段树主要有以下几个操作：

    • build(u, l, r)：建立线段树。
    • pushdown(u)：下传懒标记。
      • 懒标记为1时表示修改，为0时表示不修改【使用异或操作，记录是否需要修改】
    • f(u)：根据懒标记，修改当前节点
    • pushup(u)：用子节点的信息更新父节点的信息。
    • updateAll(u, l, r)：修改区间和，本题中是反转区间中的每个数，那么区间和 $s=r-l+1-s$。
    • query(u, l, r)：查询区间和

• 实现

  class Solution {
      public long[] handleQuery(int[] nums1, int[] nums2, int[][] queries) {
          List<Long> res = new ArrayList<>();
          int n = nums1.length;
          long sum2 = 0L;
          for (int i = 0; i < n; i++){
              sum2 += nums2[i];
          }
          SegmentTree seg = new SegmentTree(nums1);
          for (int[] q : queries){
              if (q[0] == 1){
                  seg.updateAll(1, q[1] + 1, q[2] + 1);
              }else if (q[0] == 2){
                  sum2 += 1L * q[1] * seg.query(1, 1, nums2.length);// 处理越界
              }else{
                  res.add(sum2);
              }
          }
          return res.stream().mapToLong(x -> x).toArray();
      }
  }
  class Node {
      int l, r;
      int sum;// 和 题目所要求的值
      int lazy;// 延迟修改的值
  }
  
  class SegmentTree {
      private Node[] tr;// 线段树
      private int[] nums;// 原数组
  
      public SegmentTree(int[] nums) {
          int n = nums.length;
          this.nums = nums;
          tr = new Node[n << 2];
          for (int i = 0; i < tr.length; ++i) {
              tr[i] = new Node();
          }
          build(1, 1, n);// 建树
      }
  
      private void build(int u, int l, int r) {// l,r表示当前区间 u表示当前节点编号（1,n）
          tr[u].l = l;
          tr[u].r = r;
          if (l == r) {// 若到达叶子节点
              tr[u].sum = nums[l - 1];// 存储值
              return;
          }
          // 左右递归
          int mid = (l + r) >> 1;
          build(u << 1, l, mid);
          build(u << 1 | 1, mid + 1, r);
          pushup(u);// 更新信息
      }
  	// 区间查询
      public int query(int u, int l, int r) {
           if (tr[u].l >= l && tr[u].r <= r) {
               // 在区间内，直接返回 
              return tr[u].sum;
          }
          pushdown(u);
          int res = 0;
          int mid = (tr[u].l + tr[u].r) >> 1;
          if (l <= mid) {
              res += query(u << 1, l, mid);
          }
          if (r > mid) {
              res += query(u << 1 | 1, mid + 1, r);
          }
          return res;
      }
  	
      // 区间修改:
      public void updateAll(int u, int l, int r) {
          if (tr[u].l >= l && tr[u].r <= r) {
              tr[u].lazy ^= 1;
              tr[u].sum = tr[u].r - tr[u].l + 1 - tr[u].sum ;
              return;
          }
          // 在回溯之前向下传递修改标记
          pushdown(u);
          int mid = (tr[u].l + tr[u].r) >> 1;
          if (l <= mid) {
              updateAll(u << 1, l, r);
          }
          if (r > mid) {
              updateAll(u << 1 | 1, l, r);
          }
          pushup(u);// 更新本节点信息
      }
      // pushUp函数更新节点信息, 本题是求和
      private void pushup(int u) {
          tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
      }
      // 懒加载
      private void pushdown(int u) {
      	if (tr[u].lazy == 1) {// 如果懒标记不为0，就将其下传，修改左右儿子维护的值
              f(u << 1);
              f(u << 1 | 1);
              tr[u].lazy = 0;// 向下传之后将该节点的懒标记清0
      	}
      }
      // 父节点修改时，维护子节点的更新
      private void f(int u){
          tr[u].sum = tr[u].r - tr[u].l + 1 - tr[u].sum;
          tr[u].lazy ^= 1;// 修改两次即为不修改
      }
  
  }
  

  • 复杂度
    • 时间复杂度：$O(n+m\ast logn)$
    • 空间复杂度：$O(n)$