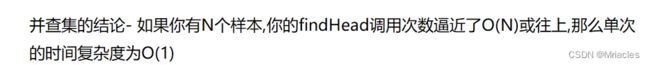并查集详解

并查集原理

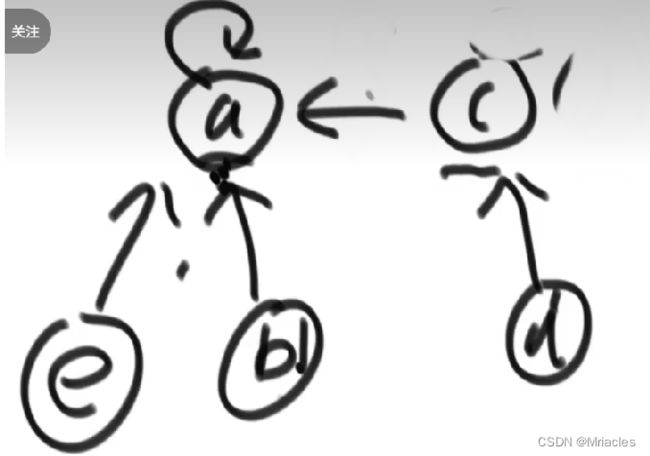
在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集
合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)

并查集一般可以解决以下问题：

1. 查找元素属于哪个集合
   沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)
2. 查看两个元素是否属于同一个集合
   沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在
3. 将两个集合归并成一个集合
   将两个集合中的元素合并
   将一个集合名称改成另一个集合的名称
4. 集合的个数
   遍历数组，数组中元素为负数的个数即为集合的个数。

并查集实现

package Union;

import java.util.HashMap;
import java.util.List;
import java.util.Stack;

public class unionFind {

    //样本进来会包一层,叫做元素
    public static class Element<V>{
        public V value;
        public Element(V value){
            this.value = value;
        }
    }
    public static class UnionFindSet<V>{
        //这个类,就是将原来单链表的图,拆成俩个哈希表来记录
        public HashMap<V,Element<V>> elementMap;
        //key 某个元素, value该元素的父亲,给一个值一一对应的元素
        public HashMap<Element<V>,Element<V>> fatherMap;
        //key是某个集合的代表元素,value是该集合的大小
        public HashMap<Element<V>,Integer> sizeMap;
        //留代表该集合的元素

        public UnionFindSet(List<V> list){
            //在初始化的时候,要求用户把样本都给你
            elementMap = new HashMap<>();
            fatherMap = new HashMap<>();
            sizeMap = new HashMap<>();
            for (V value : list){
                Element<V> element = new Element<>(value);
                elementMap.put(value,element);
                fatherMap.put(element,element);
                //任何一个元素各自成圈,大小都是1
                sizeMap.put(element,1);
            }
        }
        private Element<V> findHead(Element<V> element){
            //给定一个值,一直往上找
            Stack<Element<V>> path = new Stack<>();

            while (element != fatherMap.get(element)){
                path.push(element);
                element = fatherMap.get(element);
            }
            //找到后,将该链表的每个元素的父节点都改成element
            while (! path.isEmpty()){
                fatherMap.put(path.pop(),element);
            }
            return element;
        }

        public boolean isSameSet(V a,V b){
            if (elementMap.containsKey(a)){
                return findHead(elementMap.get(a)) == findHead(elementMap.get(b));
            }
            return false;
        }
        public void union(V a, V b){
            //俩个元素检查是否注册过
            if (elementMap.containsKey(a) && elementMap.containsKey(b)){
                Element<V>  aF = findHead(elementMap.get(a));
                Element<V>  bF = findHead(elementMap.get(b));
                if (aF != bF){
                    //如果俩个头结点不相等,找到链表值多的那一个
                    Element<V> big = sizeMap.get(aF) >= sizeMap.get(bF)? aF : bF;
                    Element<V> small = big == aF ?bF:aF;
                    //将链表值小的那个一个的顶端挂到数量多的的顶端上
                    fatherMap.put(small,big);
                    //改变size和移除size
                    sizeMap.put(big,sizeMap.get(aF)+sizeMap.get(bF));
                    sizeMap.remove(small);
                }
            }
        }
    }
}

常规解题思路

package Union;

public class Test {
    /*查找一个图中有多少个相邻的岛
    *  深度优先*/
    public static int countIslands(int[][] m){
        //时间复杂度O(M * M)
        if (m == null || m[0] == null){
            return 0;
        }
        int N = m.length;
        int M = m[0].length;
        int res = 0;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                if (m[i][j] == 1){
                    res++;
                    infect(m,i,j,N,M);
                }
            }
        }
        return res;
    }
    public static void infect(int[][] m,int i,int j,int N,int M){
        if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] == 1){
            return;
        }
        // i ,j 没有越界,并且当前的位置是一个有效位置.
        m[i][j] = 2;//不会死循环的关键
        infect(m,i+1,j,N,M);
        infect(m,i-1,j,N,M);
        infect(m,i,j+1,N,M);
        infect(m,i,j-1,N,M);

    }
    //并查集解决

}

这个岛使用并查集的解法-最大的优点就是不局限于一台CPU了,

547. 省份数量

public int findCircleNum(int[][] isConnected) {
      int n = isConnected.length;
      UnionFindSet ufs = new UnionFindSet(n);
      for(int i = 0;i < isConnected.length;i++) {
         for(int j = 0;j < isConnected[i].length;j++) {
      //表示第i个城市和第j个城市相邻，那么就合并
            if(isConnected[i][j] == 1) {
              ufs.union(i,j);
            }
        }
     }
    return ufs.getCount();
  }

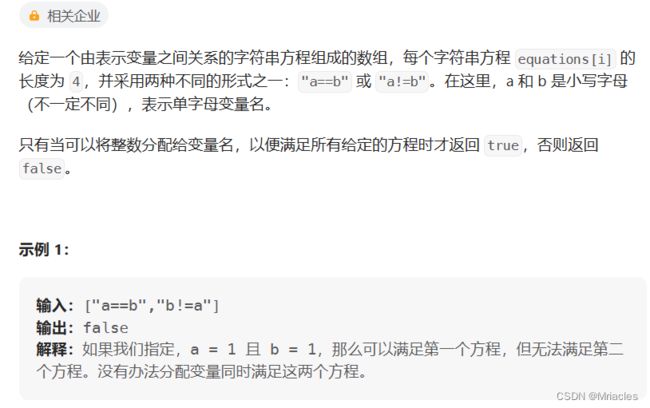
990. 等式方程的可满足性

/*
解题思路：
1. 将所有"=="两端的字符合并到一个集合中
2. 检测"!=" 两端的字符是否在同一个结合中，如果在不满足，如果不在满足
*/
class Solution {
	public boolean equationsPossible(String[] equations) {
		UnionFindSet ufs = new UnionFindSet(26);
		for(int i = 0; i < equations.length; ++i) {
		// 将等号两端的字符合并到一个集合中
			if('=' == equations[i].charAt(1)){
				ufs.union(equations[i].charAt(0)-'a',equations[i].charAt(3)-'a');
			}
		}
		for(int i = 0; i < equations.length; ++i){
		// 将等号两端的字符合并到一个集合中
			if('!' == equations[i].charAt(1)) {
		// 如果"!="两端的字符在同一个集合中，不满足
				int root1 = ufs.findRoot(s.charAt(0)-'a');
				int root2 = ufs.findRoot(s.charAt(3)-'a');
				if(root1 == root2) return false;
			}
		}
		return true;
	}
}