红黑树创建和插入—C语言
红黑树的创建和插入—C语言
红黑树的删除
绝望ing……
- 先知道红黑树是啥:每个节点带颜色(红/黑)的二叉查找树。
- 红黑树的特性:①每个节点非红即黑;②根和叶子(哨兵NIL)是黑色;③每个红色节点的俩娃都是黑色;④每个节点到其所有后代叶节点的简单路径,包含相同数量黑色结点。

3.红黑树的C的实现:基本操作是插入、删除、旋转(左旋、右旋)。
基本定义
#define RED 0
#define BLACK 1
//定义红黑树结点
typedef struct RBTreeNode
{
char color;//颜色
int key;//值
struct RBTreeNode *lchild;//左孩子
struct RBTreeNode *rchild;//右孩子
struct RBTreeNode *parent;//父结点
}Node,*RBTree;
//定义红黑树根结点
typedef struct rb_root
{
Node *node
} RBRoot;左旋
该结点变成它右孩子的左结点。
//>﹏<左旋右旋指针指向真的要搞搞清楚,后来程序出错改了好久55555。

代码实现:
//左旋
void rbtree_left_rotate(RBRoot *root,Node *x)
{
Node *y=x->rchild;//设置x的右结点等于y
//首先,先找到y的左孩子,它最终被x收养为右孩子
x->rchild=y->lchild;
if (y->lchild!= NULL)
y->lchild->parent = x;
y->parent=x->parent;
//x->rchild=y->lchild;
//y->lchild->parent=x;
//y缺了左孩子,x成为y的左孩子
if(x->parent==NULL)//当x为根结点的时候
{
root->node=y;//将y设为根结点
}
else//当x不是根节点的时候
{
//y->parent=x->parent;//y接替x做别人的儿子
if(x->parent->lchild==x) //要确定y是做的左孩子还是右孩子
{
x->parent->lchild=y;
}
else
{
x->parent->rchild=y;
}
}
y->lchild=x;//x就位
x->parent=y;
}右旋
该结点变成它左孩子的右结点。
代码实现:
//右旋
void rbtree_right_rotate(RBRoot *root,Node *y)
{
Node *x=y->lchild;
y->lchild=x->rchild;
//找到x的右孩子,它最终被y收养为左孩子
if(x->rchild!=NULL)
{
x->rchild->parent=y;
}
x->parent=y->parent;
//此时x的右孩子是空的,y来当x的右孩子
if(y->parent==NULL)//如果y为根结点
{
root->node=x;//将x设为根节点
}
else//当y不是根节点的时候
{
//y->parent=x->parent;//x接替y做别人的儿子
if(y->parent->rchild==y) //要确定x是做的左孩子还是右孩子
{
y->parent->rchild=x;
}
else
{
y->parent->lchild=x;
}
}
x->rchild=y;//y就位
y->parent=x;
}插入
先像一个普通的二叉查找树一样将结点插入,颜色设为红色(为了不影响性质④),然后进行调整。
插入的代码实现:
//插入
void rbtree_insert(RBRoot *root,Node *node)
{
Node *y=NULL;
Node *x=root->node;
while(x!=NULL)//x为叶子结点跳出循环
{
y=x;
if(x->key>node->key)
{
x=x->lchild;
}
else
{
x=x->rchild;
}
}
node->parent=y;
if(y!=NULL)
{
if(node->key<y->key)
{
y->lchild=node;
}
else
{
y->rchild=node;
}
}
else
{
root->node=node;//若y为NULL,说明树为空,则将node设为根节点
}
node->color=RED;//将颜色设为红色
//插入修正
rbtree_insert_fixup(root, node);
} 插入修正
我们这里需要分析这里插入的结点N的父节点,爷爷节点,和叔叔节点,总结如下:

代码实现:
void rbtree_insert_fixup(RBRoot *root, Node *node)
{
Node *parent, *gparent;
// 若父节点存在,并且父节点的颜色是红色
while ((parent = node->parent) && (parent->color==RED))
{
gparent = parent->parent;
//若“父节点”是“祖父节点的左孩子”
if (parent == gparent->lchild)
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->rchild;
if (uncle && uncle->color==RED)
{//父、叔变黑,爷变红,对爷进行判断
uncle->color=BLACK;
parent->color=BLACK;
gparent->color=RED;
node = gparent;
continue;
}
}
// Case 2条件:叔叔是黑色,且当前节点是右孩子
if (parent->rchild == node)
{
Node *tmp;
rbtree_left_rotate(root, parent);//父左旋
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是左孩子。
parent->color=BLACK;
gparent->color=RED;
rbtree_right_rotate(root, gparent);
}
else//若“z的父节点”是“z的祖父节点的右孩子”
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->lchild;
if (uncle && (uncle->color==RED))
{
uncle->color=BLACK;
parent->color=BLACK;
gparent->color=RED;
node = gparent;
continue;
}
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子
if (parent->lchild == node)
{
Node *tmp;
rbtree_right_rotate(root, parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子。
parent->color=BLACK;
gparent->color=RED;
rbtree_left_rotate(root, gparent);
}
}
// 将根节点设为黑色
root->node->color=BLACK;
}然后就是根据一个数组建造一个红黑树,并插入一个数进行调整的完整代码:
#include<stdio.h>
#include<stdlib.h>
#define RED 0
#define BLACK 1
//定义红黑树结点
typedef struct RBTreeNode
{
char color;//颜色
int key;//值
struct RBTreeNode *lchild;//左孩子
struct RBTreeNode *rchild;//右孩子
struct RBTreeNode *parent;//父结点
}Node,*RBTree;
//定义红黑树根结点
typedef struct rb_root
{
Node *node;
} RBRoot;
//创建红黑树,返回红黑树的根
RBRoot* creat_rbtree()
{
RBRoot *root=(RBRoot*)malloc(sizeof(RBRoot));//定义根结点,并分配空间
root->node=NULL;//初始化
return root;
}
//新建一个结点
Node* creat_rbtree_node(int key,Node *parent,Node *lchild,Node *rchild)
{
Node* p;
p=(Node*)malloc(sizeof(Node));
p->key=key;
p->lchild=lchild;
p->rchild=rchild;
p->color=BLACK;
return p;
}
//左旋
void rbtree_left_rotate(RBRoot *root,Node *x)
{
Node *y=x->rchild;//设置x的右结点等于y
//首先,先找到y的左孩子,它最终被x收养为右孩子
x->rchild=y->lchild;
if (y->lchild!= NULL)
y->lchild->parent = x;
y->parent=x->parent;
//x->rchild=y->lchild;
//y->lchild->parent=x;
//y缺了左孩子,x成为y的左孩子
if(x->parent==NULL)//当x为根结点的时候
{
root->node=y;//将y设为根结点
}
else//当x不是根节点的时候
{
//y->parent=x->parent;//y接替x做别人的儿子
if(x->parent->lchild==x) //要确定y是做的左孩子还是右孩子
{
x->parent->lchild=y;
}
else
{
x->parent->rchild=y;
}
}
y->lchild=x;//x就位
x->parent=y;
//printf("(对关键字%d进行左旋)",x->key);
}
//右旋
void rbtree_right_rotate(RBRoot *root,Node *y)
{
Node *x=y->lchild;
y->lchild=x->rchild;
//找到x的右孩子,它最终被y收养为左孩子
if(x->rchild!=NULL)
{
x->rchild->parent=y;
}
x->parent=y->parent;
//此时x的右孩子是空的,y来当x的右孩子
if(y->parent==NULL)//如果y为根结点
{
root->node=x;//将x设为根节点
}
else//当y不是根节点的时候
{
//y->parent=x->parent;//x接替y做别人的儿子
if(y->parent->rchild==y) //要确定x是做的左孩子还是右孩子
{
y->parent->rchild=x;
}
else
{
y->parent->lchild=x;
}
}
x->rchild=y;//y就位
y->parent=x;
//printf("(对关键字%d进行右旋)",y->key);
}
//插入修正
void rbtree_insert_fixup(RBRoot *root, Node *node)
{
Node *parent, *gparent;
// 若父节点存在,并且父节点的颜色是红色
while ((parent = node->parent) && (parent->color==RED))
{
gparent = parent->parent;
//若“父节点”是“祖父节点的左孩子”
if (parent == gparent->lchild)
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->rchild;
if (uncle && uncle->color==RED)
{//父、叔变黑,爷变红,对爷进行判断
uncle->color=BLACK;
parent->color=BLACK;
gparent->color=RED;
node = gparent;
continue;
}
}
// Case 2条件:叔叔是黑色,且当前节点是右孩子
if (parent->rchild == node)
{
Node *tmp;
rbtree_left_rotate(root, parent);//父左旋
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是左孩子。
parent->color=BLACK;
gparent->color=RED;
rbtree_right_rotate(root, gparent);
}
else//若“z的父节点”是“z的祖父节点的右孩子”
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->lchild;
if (uncle && (uncle->color==RED))
{
uncle->color=BLACK;
parent->color=BLACK;
gparent->color=RED;
node = gparent;
continue;
}
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子
if (parent->lchild == node)
{
Node *tmp;
rbtree_right_rotate(root, parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子。
parent->color=BLACK;
gparent->color=RED;
rbtree_left_rotate(root, gparent);
}
}
// 将根节点设为黑色
root->node->color=BLACK;
//printf("对关键字%d进行插入修正",node->key);
}
//插入
void rbtree_insert(RBRoot *root,Node *node)
{
Node *y=NULL;
Node *x=root->node;
while(x!=NULL)//x为叶子结点跳出循环
{
y=x;
if(x->key>node->key)
{
x=x->lchild;
}
else
{
x=x->rchild;
}
}
node->parent=y;
if(y!=NULL)
{
if(node->key<y->key)
{
y->lchild=node;
}
else
{
y->rchild=node;
}
}
else
{
root->node=node;//若y为NULL,说明树为空,则将node设为根节点
}
node->color=RED;//将颜色设为红色
//插入修正
rbtree_insert_fixup(root, node);
}
int insert_rbtree(RBRoot *root,int key)
{
Node *node;//新建一个结点
node=creat_rbtree_node(key,NULL,NULL,NULL);
if(node==NULL) return -1;
else rbtree_insert(root,node);
return 0;
}
/*
* 中序遍历"红黑树"
*/
void inorder(RBTree tree)
{
if(tree != NULL)
{
inorder(tree->lchild);
printf("%d", tree->key);
if(tree->color==0)
{
printf("(RED) ");
}
else
{
printf("(BLACK) ");
}
inorder(tree->rchild);
}
}
void inorder_rbtree(RBRoot *root)
{
if (root)
inorder(root->node);
}
int main()
{
int a[10]={5,3,6,7,4,1,2,8,10,9};
int i;//计数器
int key;
int n=sizeof(a)/sizeof(int);
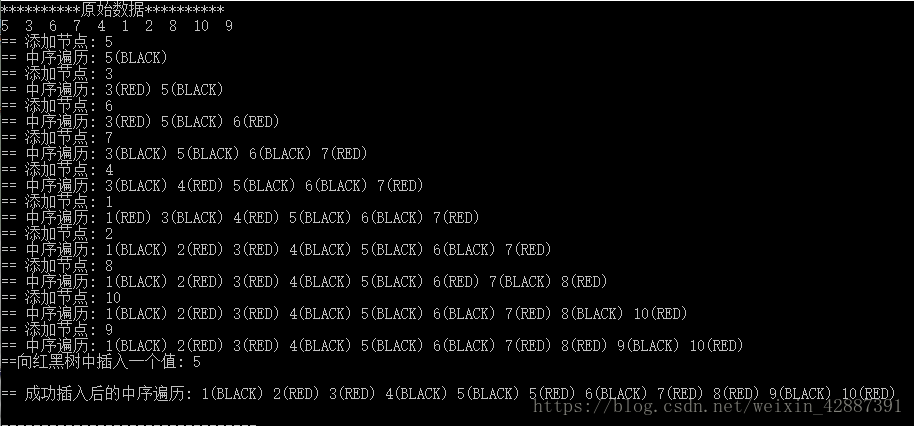
printf("**********原始数据**********\n");
for(i=0;i[i]);
}
printf("\n");
//下面开始创建红黑树
RBRoot *root=NULL;//首先创建红黑树的根
root=creat_rbtree();
for(i=0;i[i]);
insert_rbtree(root,a[i]);
printf("== 中序遍历: ");
inorder_rbtree(root);
printf("\n");
}
printf("==向红黑树中插入一个值: ");
scanf("%d",&key);
insert_rbtree(root,key);
printf("\n== 成功插入后的中序遍历: ");
inorder_rbtree(root);
printf("\n");
return 0;
}
总结:虽然代码都是自己理解后,参考了许多人的代码对照敲下来的,但并不是自己。希望自己下次理解透彻后可以自己尝试敲一遍。明天继续红黑树的删除。
做一个弱鸡我是认真的。
参考