2020.10月做题记录

PS:本博客仅选择了一些作者认为有必要记录的题目进行记录。

week -1

2020.09.28-2020.10.4

军训+国庆放假…就这样又废了一周…

2020.10.04

回来第一天完全没有状态…什么题都不会做了…

[LOCAL]买萝卜（carrot）

随便贪心一下就好了…
有兔子在买萝卜我们就直接买，剩下的括号匹配贪心一下即可。
复杂度：$O(n)$。

[LOCAL]游戏（game）

显然我们可以采用并查集来合并点，但是我们与此同时也需要合并这些点相邻的边的信息。
如果我们采用vector合并，复杂度会过高，无法通过。
注意到我们的邻接表本事就是一个链表结构，而它的合并是 $O(1)$ 的，因此可以解决这个问题。

[LOCAL]礼物（gift）

不想写了，简单说一下。
首先我们根据分析得到 $k=1$ 时的排列情况，注意到最后几位乱填的方案数为${\prod }_{i=x}^n\min \{m,n-i+1\}$，由于 $k\le 10^{16}$，那么它最多影响 $O(lo{g}_{m}k)$ 位数，那么我们就可以考虑直接暴力构造。构造的方法就是枚举当前位以及当前位现在填了什么，再算一下填完了之后后面总共的可能的方案数，如果范围正好包含了 $k$ ，我们就接着填下一个数。
复杂度:$O(n+lo{g}_m^{3}k)$

[LOCAL]煎蛋的疑惑（excatalan）

很容易猜到但是是一个相当重要的思想。
根据我们括号匹配的机制来看，我最少不能匹配的括号对即为最小括号深度的相反数。
我们把它转到网格图上，那么方案数的另一个含义就是不能越过 $y=x+m$ 这条对角线，但必须经过的走到 $(n,n)$ 的线路方案数。
这里我们需要沿用卡特兰数的计算方法[详解链接]。
我们将计算时不能经过的线改成 $y=-m-1$ 即可。
这样我们就可以证明答案就是：$$\left(\genfrac{}{}{0ex}{}{n-m}{2n}\right)-\left(\genfrac{}{}{0ex}{}{n-m-1}{2n}\right)$$

[LOCAL]数据结构（set）

我们每次操作需要将 $x^k$ 变为 $(x+1{)}^k$，这很容易让我们联想到公式：
$$(x+1{)}^k=\sum _{i=0}^k(\genfrac{}{}{0ex}{}{i}{k})x^i$$
怎么利用这个公式呢？我们需要利用x变化时的不变之处，也即是无论x如何变，其总可以表达为 ${\sum }_{i=1}^k\left(\genfrac{}{}{0ex}{}{i}{k}\right)f_i$ 的形式。
这使得我们可以将全部x一起考虑。
具体来说，定义 $su{m}_i=\sum x^i$，那么一次整体加一操作带来的变化就是：
$$su{m}_i^{\prime }=\sum _{j=0}^i\left(\genfrac{}{}{0ex}{}{j}{i}\right)su{m}_j$$
而插入一个数也可以 $O(nk)$ 完成。
因此复杂度是 $O(n{k}^2)$ 的。
但是本题还有更优秀的做法：
假设我们现在已经过了 $t$ 次加一操作。
我们可以维护:
$$\sum _{i=0}^k\left(\genfrac{}{}{0ex}{}{i}{k}\right)d^i{f}_i$$
其中 $f_i$ 是$\sum x^{k-i}$ 的和即可。
加入数字的时候我们就假设加入的是 $(x-t)$ 即可。
复杂度：$O(nk)$ 。

[LOCAL]博弈（game）

真做不来这种博弈题。
结论是最后剩下的数一定是最中间的 2 到 3 个数的 $\max$ 或 $\min$（具体取决于序列长度的奇
偶性）。
这大概是因为两人的策略可以抵消持平，这样不管怎样都只能取中间的数。
然后随便做就可以了。

[LOCAL]植物大战僵尸（pvz）

只要注意到前面的僵尸可以为后面的僵尸提供 $\log p_i$ 次向前的机会，而不是完全无关，因此我们只要找到一个方法使得分配到某一行的僵尸最后能够剩下即可，接下来我们可以用一个背包dp轻松完成。

week 1

2020.10.5-2020.10.11

军训+国庆放假又废了一周…

2020.10.05

状态还是很差…思博题都要调半天…

[LOCAL]旅行（trip）

原题:D-Points Construction Problem

给你 $n$ 个$1\times 1$ 的正方形，求构造一个周长恰好为 $m$ 的图形的方案。

首先周长显然应该是个偶数，接下来我们可以分成三个部分进行构造：

• $m>4n$：显然无解。

• $2(n+1)\le m\le 4n$：考虑把正方形分成连续一列+若干个单独的正方形，计算可得单独的正方形为$\frac{m-2(n+1)}{2}$个。

• $m<2(n+1)$：考虑一个 $(1,1)-(x,y)$ 的长方形，注意到我们挖去一个$(2,2)-(x,y)$且包含$(x,y)$的连通块周长不变，那么我们就可以先摆好$(1,1),(1,2),\dots ,(1,x),(2,1),\dots ,(y,1)$的正方形，然后再往里面尽量补充。如果填满了就输出无解，可以简单证明这里的无解判断是充分的(证明略去)。

  复杂度:$O(n)$。

[LOCAL]树上的堆（heap）

原题:CF955F Heaps
没什么原因，就是做不来这种题…
一看完题目就想 树链剖分+线段树 开搞

首先有一个经典的性质：如果我们从小到大枚举 $k$ ，每次只遍历度数大于 $k$ 的点，复杂度是 $O(n)$的。可以根据 ${\sum }_{k=1}^n{\sum }_{i=1}^n[de{g}_i\ge k]={\sum }_{i=1}^{n}de{g}_i=2n-2$ 轻松得到。
接下来显然还有两个性质：
$$\begin{gathered} 1.d(u,k)\le {\log }_{k}n \\ 2.d(u,k)\ge d(u,k+1) \end{gathered}$$
$k=1$ 的答案显然就是每个点的最大向下深度，我们现在只考虑 $k>1$ 的情况：
首先我们考虑先处理好 $d(u,k)$，由于要找的树深度最多是 $O({\log }_{2}n)$级别的，这意味着我们可以直接定义 $d{p}_{u,d}$ 表示向下树深度为 $d$ 时 $k$ 的最大值为多少，转移的时候我们排序处理一下即可，这样做最坏是 $O(n{\log }^{2}n)$的，但显然远远达不到这个复杂度。
现在我们已经处理完了 $d(u,k)$ ，我们需要求出 $sd(u,k)$ 就可以了。
然后就是本题很降智的部分（真没想到）：
注意到前面提到的两个性质，因为 ${\sum }_{i=1}^{n}sd(i,2)\le n{\log }_{2}n$，又有 $sd(u,k)\ge sd(u,k+1)$ 那么如果我们从 $k=n$ 开始枚举，$sd(u,k)$ 的总变化量是 $O(n{\log }_{2}n)$ 的，因此我们直接暴力爬树更新答案就可以做到 $O(n{\log }_{2}n)$了。
复杂度：$O(n{\log }^{2}n)$。

[LOCAL]神秘的信（letter）

原题:H-Sort the Strings Revision
考虑我们修改完了第一个位置，那么后面的串的字典序一定会全部大于/小于前面生成的串，二者之间互不影响。
这让我们联想到了笛卡尔树，但也并不完全是，因为当前操作修改完的串并没有确定和后面的串的字典序关系，因此我们需要在输出的时候采用一些特殊的技巧。
本题还需要我们考虑 $d_i=p_i\mathrm{m}\mathrm{o}\mathrm{d}10$ 的情况，一个简单的实现方法就是将当前的 $p_i$ 值改成 INF ，最后递归输出的时候遇到这种权值就直接输出即可。
建完笛卡尔树后具体实现如下:

void solve(int x,int l,int r){
    if(p[x]==INF||l>=r){
        for(int i=l;i<=r;i++)ans[i]=num++;
        return ;
    }
    if(d[x]>p[x]%10)solve(lc[x],l,x),solve(rc[x],x+1,r);
    else solve(rc[x],x+1,r),solve(lc[x],l,x);
}

复杂度：$O(n)$ 。

CF1423F Coins

很巧妙的构造势能函数的题目。
首先显然只有人数恰好与环长相同的情况才会出现无解。
只要我们能够想到一种方法使得操作若干次后其势能值不会变，且其与最终状态的势能值不同这道题目就可以解决了。
构造方法就是:
$E(x)=({\sum }_{i=1}^{n}po{s}_i\times nu{m}_i)\mathrm{m}\mathrm{o}\mathrm{d}n$
$po{s}_i$ 表示当前位置，$nu{m}_i$ 表示当前位置上有多少人。
可以尝试一下为什么它是定值。

2020.10.06

[LOCAL]遗忘之祭仪（prepare）

一开始没看到只能覆盖一次以为T1连NTT都来了。
首先显然可以得到一个 $O(nmab)$，即枚举左上角，每次检验是否和图形完全同构。
仔细思考一下，如果答案是Yes那么我们只要检验失败就一定会是第一个位置失败，那么这样我们的复杂度实际上就是 $O(nm)$ 的。
再考虑 No 的情况，由于是 Yes 检验失败就一定会是第一个位置失败，那么在某个位置不是时我们就可以直接退出即可，复杂度也是 $O(nm)$。
事实上数据特别水，随便写个 $O(nmab)$ 的暴力加个break就过了…

[LOCAL]客星璀璨之夜（stars）

做过一遍，实际上没有太懂及其晦涩的题解的意思，结果就又做不来了。
本来如果按照自己的做法大概还有$O(n^3)$的分吧…

首先容易发现的是我们的答案和每个点的位置没有太大关系，我们只需要求出这些位置被划分出的每一段的期望经过次数即可。
其次，我们会发现当一个小球进洞之后，接下来的问题无异于一个 $n-1$ 个球 $n$ 个洞的同样的问题——这意味着我们找到了等价状态，因此我们可以使用动态规划来解决做这个问题。
因此我们定义 $f_{L,R,0/1}$ 表示现在一共有 $L+R+1$ 个球，我们现在要计算第 $L+1$ 个球和它左边/右边的洞口这一段期望会被经过的次数。
由于我们是从球数从小到大这样计算的，那么这等价于每次会存在一个求莫名其妙的从一个洞和一个球的空隙中冒出来，然后往球或洞的方向滚动一段距离并停下来。
一个显然的做法是，我们可以枚举这个球这次会从哪个空隙中冒出来，这样就是一个 $O(n^3)$ 的做法。但是注意到如果我们的球不是从当前球的两边的空隙冒出来的话，我们只会影响当前 dp 值的编号，而不会增加覆盖次数，因此我们可以放在一起考虑，这样就是一个 $O(n^2)$ 的解法了!
先计算加入球在两边的情况:
$$f_{i,j,0/1}=\frac{i}{i+j+1}{f}_{i-1,j,0/1}+\frac{j}{i+j+1}{f}_{i,j-1,0/1}$$
再计算加当前球的两边的空隙冒出来的情况:
$$\begin{gathered} f_{i,j,0}=\frac{1}{2(i+j+1)}(f_{i-1,j,1}+1+f_{i,j-1,0}) \\ {f}_{i,j.1}=\frac{1}{2(i+j+1)}(f_{i-1,j,0}+f_{i,j-1,1}+1) \end{gathered}$$
最后我们再对每个答案乘上 $x_i-x_{i-1}$ 即可。
复杂度：$O(n^2)$。

[LOCAL]割海成路之日（sea）

其实是一个非常套路的题目，然而我以为tly出比赛会把T3设成10KB的那种题目…想到了也不是很敢写…

注意到边的状态只会下降不会上升，那么显然我们可以使用两个并查集，一个并查集仅并上权值为$1$的边，一个并查集并上权值为$1,2$的边。
那么我们可以把题目看成一个仅有 $1,2$ 两种边的树，且我们要统计的答案一定会呈现父亲-儿子这样的关系，这种关系有一个非常关键的技巧：我们只考虑儿子对父亲这样的关系的计算，而对父亲对儿子这样的关系我们转化成前面一种关系单独计算。
现在我们需要解决题目给出的两种问题:

• 统计有多少个点可以到达 $S$：考虑对 $S$ 点权值为 $3$ 的边的儿子，他们会对父亲产生一些贡献，我们用一个数组 $f_s$ 来提前预处理计算这些贡献，而这些贡献可以在修改儿子状态时快速维护。而对于$S$ 点到父亲的答案，我们单独计算即可。

• 判断 $S$ 到 $T$ 的可达性：和 LCA 的解决方法类似，如果 $S$ 是 $T$ 的儿子，那么我们判断 $fa[S]$ 和 $T$ 是否在同一连通块即可，如果 $S$ 是 $T$ 的父亲，那么我们倒过来，判断 $fa[T]$ 和 $S$ 是否在同一连通块即可。

  注意由于题目规则，这里的连通块含义不尽相同($A$或者$B$)，因此代码细节很多，写的时候一定要仔细思考。
  注意到并查集不能按秩合并，因此最坏复杂度是 $O(n\log n)$。

2020.10.07-10

补之前的博客+月考

2020.10.11

CSP-S 初赛爆炸日…
nth_element 的复杂度分析错了，结果错了一堆选择题（可怜）。

week 2

2020.10.12-2020.10.18

月考没有悬念的又考挂了…

2020.10.12

CF1408E Avoid Rainbow Cycles

想了半天代价为 $a_i+b_j$ 有什么性质…结果…
其实题目就是让我们求一个连通

CF1408G Clusterization Counting

发现这题就是Kruskal 重构树模型就做完了…

2020.10.13-14

又在补之前的博客+复习之前考试的题目…

2020.10.15-16

ARC104-C Fair Elevator

就是个细节题…
定义 $f_i$ 表示只考虑 $[1,2i]$ 时是否存在合法方案，那么我们每次向后扩展一个合法区间即可。
现在问题的关键就变成了判断一个区间是否合法：
首先我们忽略 -1 -1 这种情况，在判断区间 $[l,r]$ 时我们仅考虑有一个端点在区间内的电梯，然后我们将 -1 的位置填上再判断一遍即可。
一定要注意自己代码的逻辑顺序!
复杂度：$O(n^3)$

ARC104-D Multiset Mean

一道英语阅读题???
考虑题目的代数含义:
$$\frac{{\sum }_{i=1}^n{a}_i\times i}{{\sum }_{i=1}^n{a}_i}=x$$
考虑移项:
$$\sum _{i=1}^n{a}_i\times (i-x)=0$$
这提示我们题目相当于将权值划分为正负两个部分，且它们的权值相等。
而这个我们可以定义 $f_{i,S}$ 为完成了前 $1,\dots ,i$ 个数，现在的加权和为 $S$ 时可选方案数。
而这可以使用前缀和优化dp做到 $O(n^{3}k)$ 。

ARC104-E Random LIS

[待填]

2020.10.17

考试看错题，直接起飞…
下午最后四十分钟去计蒜客模拟赛水了两道签到题，结果时间有点少挂题了…
结果作死掉了Rating

[LOCAL]异或（xor）

无聊的不能再无聊的模拟题…

[LOCAL]最大公约数（gcd）

最近不大自信，没有敢往枚举 gcd 的方向想…结果一直在原地徘徊…
事实上把区间max和gcd合在一起的这种题本来就没有什么好的性质，那么我们就必须利用答案是最大数的质因数这个性质进行优化，其它的优化必定是徒劳的。

首先我们可以轻松设计出一个转移方程:
$$f_{i,j}=\gcd \{f_{k,j-1},\underset{p=k+1}{\overset{i}{\max }}{a}_p\}$$
直接做是 $O(n^{2}k)$ 的。
注意到答案一定是最大数的质因数，考虑枚举答案。
这样做看上去只会增加复杂度，但是注意到此时我们只需要判断答案的可行性，而合法区间显然是一个前缀+一个后缀，那么这样我们就可以直接使用前缀和+差分优化了。
复杂度:$O(d(a_i)nk)$。
不知道为什么，笔者感觉这类利用状态是 0/1 就能前缀和/bitset 优化的题目特别难凭借直觉预判到，可能也只能通过不断的尝试才能得到合理的优化方法吧…

[LOCAL]树上游戏（game）

成功读错题…
本来五分钟就能够解决的问题想了整场考试…

原题等价于在一颗由若干条拼在一个点上的链组成的树，在点上安排一些权值能否满足 $a_x<a_{f{a}_x}$ 。
这个随便贪心做一做就可以了。

[LOCAL]时代的眼泪（tears）

基本上就是个树套树板题。

2020.10.18

参加LGR078，排名还可以。
但是LGR对我这种常数巨大的选手来说实在是太不公平了…

[LGR 078]蝴蝶与花

做比赛的时候看到很少人过以为这题很难，然后发现其他同学想出来以后想了5分钟就会了…

[以下是简略题解]
我们先尽量找一个 $[1,p]$ 的区间使得权值和大于要求的和且 $p$ 最小，显然两者之间最多相差一。
接下来我们只需要向后滑动窗口，只要我们将一个 $2$ 换成一个 $1$ 就达到要求了，而这个我们可以用线段树的一些操作来解决。

[LGR 078]象棋与马

论想到做法却算错了时间复杂度是怎样的一种感受.jpg

通过简单打表或者证明可以得到：
$$\sum _{i=1}^n\sum _{j=1}^{n}p(i,j)=\sum _{i=1}^n\sum _{j=1}^n[gcd(i,j)=1][2\nmid i+j]$$
然后开始反演:
$$\sum _{2\nmid p}\mu (p)\times (2\lceil \frac{p}{2}\rceil \lfloor \frac{p}{2}\rfloor )$$
然后我们很容易想到用杜教筛解决，但是我们需要求$S_n={\sum }_{2\nmid p}^n\mu (p)$的值。
直接杜教筛显然是无法完成的，我们只能求 $P_n={\sum }_p^n\mu (p)$。
因此我们现在考虑求 $T_n={\sum }_p^n\mu (2p)$。
那么显然有：
$S_n=P_n-T_{\lfloor \frac{n}{2}\rfloor }$
注意到 $T_n$ 中如果 $i\mid 2$，那么它就是 $4$ 的倍数，$\mu (i)$ 一定为 $0$，这使得我们可以与 $S_n$ 建立联系：
$$\begin{gathered} T_n=\sum _{2\nmid p}^n\mu (2p) \\ =\mu (2)\sum _{2\nmid p}^n\mu (p) \\ =-S_n \end{gathered}$$
那么就有：
$$S_n=P_n+S_{\lfloor \frac{n}{2}\rfloor }$$
我们现在就$O(\log n)$可以递归计算了。
实际上这个递归本质上就是一个反演。
这个算法的复杂度很玄，看上去是$O(\sqrt{n}\log n\times n^{\frac{2}{3}})$的，错失AK机会。
这个做法通过的关键原因是我们在杜教筛中进行了记忆化，这使得整数分块套整数分块之后复杂度不会变。
因此本题复杂度至少是$O(n^{\frac{2}{3}}\log n)$的（也有可能是$O(n^{\frac{2}{3}})$）。
不过这道题的复杂度就好像不能用这样的思想计算。

[Nowcoder 1]牛牛的凑数游戏

其实是一个结论题。
注意到部分分有：

对于另$10\%$的测试数据，保证输入的$a_i$单调非降。
对于另$10\%$的测试数据，保证输入的$a_i$为$2$的非负整数幂。

从这两个结论入手打表找到结论就是将集合排序满足 ${\sum }_{i=1}^p{a}_i<a_{p+1}$ 的最小 $p$，${\sum }_{i=1}^p{a}_i$ 就是答案。

证明:[待填]

知道这个之后很容易发现就是个主席树板题。

week 3

2020.10.19-2020.10.25

突然发现CSP-S2又神奇的与半期考试无缝接在了一起[已去世]

2020.10.20

ARC104F Visibility Sequence

[待填]

2020.10.21

本来想做做牛客的比赛的，结果发现两天都是一堆模板题…

ARC105D Let’s Play Nim

[待填]

ARC105C Camels and Bridge

首先枚举骆驼的排列情况计算。
然后我们反过来想，如果有连续的一段骆驼重量大于某个桥的承重，那么他们之间的距离就应大于等于这个桥的长度。
写成不等式就是：
$$L_i\le x_r-x_{l-1}$$
我们求两端的骆驼的最短距离就是差分约束，用最长路解决即可。
接下来我们只需要利用单调性使得有用的边数为 $O(n^2)$ 级别即可。
而这个我们可以利用lower_bound解决。
复杂度：$O(n!n^2\log n)$。

2020.10.22

[已隐藏]

2020.10.23

[已隐藏]

2020.10.24

感觉时间非常不够用…前面签到题好难，想了好久都没想到…但是大佬却随随便便就AC了…
难道和我前一天1点半睡有关系？

[LOCAL]过河（river）

其实只需要想到青蛙可以一个一个往后跳而不是$m$ 只青蛙成为一个整体跳跃就不会出现贪心错误。
那么答案显然就是距离为 $D$ 的一段区间中包含石子数量最少的数量，滑窗即可。
复杂度：$O(n)$

[LOCAL]选数（choose）

今天首先做出来的题目.jpg
注意到：$P(x)=(\lfloor \frac{2x}{2^n}\rfloor +2x)\mathrm{m}\mathrm{o}\mathrm{d}{2}^n$ 就是向左循环移位。那么我们反过来想就是小 S 取的部分向左循环移位。
然后我们将每一个可能的状态表示成 $P(pr{e}_i)⨁su{f}_{i+1}$，然后将其插入 tire 树中。
然后我们要求的就是 $\min (x⨁P(pr{e}_i)⨁su{f}_{i+1})$ 。
而这个可以简单的用 dfs 解决。
复杂度：$O(nm)$。
注意 tire 树空间也是 $O(nm)$ 级别的。

[LOCAL]模板（ac）

[待填]

2020.10.25

[jsk 02]魔法阵（magic）

永远不会组合数学.jpg

考虑魔法对个数可以表示成 $p=n-k-d$

[jsk 02]平均数（average）

[ARC065D]Shuffling

容易发现我们的方案数只受

2020.10.26

[ARC066C]Addition and Subtraction Hard

容易发现只会在 + 后加括号和括号最多 3 层两条性质，然后 dp 即可。

[ARC067C]Grouping

非常容易通过广义组合数得到一个 $O(n^3)$ 的dp。
但是仔细思考会发现由于后两个枚举项乘积 $\le n$ 因此实际上是 $O(n^2\log n)$ 级别的。

[ARC070B]No Need

显然我们需要使得其他数表达不出 $[k-a_x,k)$ 中的任何一个数就可以了，我们当然可以直接用背包撤回技巧直接做到 $O(NK)$ 。
不过注意到题目是存在单调性的，这意味这我们将 $a_i$ 排序后就可以二分 $x$ 。
可以做到 $O(NK\log N)$。
注意到还可以 bitset 优化，因此是 $O(\frac{NK\log N}{w})$ 。

[ARC067D]Yakiniku Restaurants

做过的题，当时搞的分治现在也还是只会分治…
事实上一个单调栈就解决了…
简单来说我们就只需要利用后缀最大值的分布情况每次从 $i$ 到 $i-1$ 改变的状态是一个区间，我们利用这个性质就能做到 $O(nm)$ 。

[ARC070C]NarrowRectangles

我太菜了…一直在想怎么用贪心优化 dp ，结果是…

2020.10.27

[ARC097C]Sorted and Sorted

关键在于确定黑白两种球的排列相对顺序。
定义 $dp[a][b]$ 表示现在已经确定了前 $a+b$ 个球，其中有 $a$ 个是黑球，有 $b$ 个是白球的最小逆序对个数。
那么转移时考虑预处理加一个数会产生多少个逆序对，可以 $O(n^2)$ 预处理。
复杂度：$O(n^2)$。

[ARC096B]Static Sushi

为什么题单上会出现这种题。
显然走一段前缀+一段后缀，记录一下最大前缀和/最大后缀和即可。

2020.10.28

[ARC095C]Symmetric Grid

真就一道阴间搜索题。
考虑枚举一个行的匹配关系，然后列的匹配关系就基本确定了。
复杂度大概是 $O((n-1)!!n{m}^2)$ 。
具体实现时我们枚举列也可以直接枚举匹配，这和 check 的复杂度没多大区别。

2020.10.29

[已隐藏]

2020.10.30

P5017 摆渡车

实际上我觉得这题比17年那道跳房子难了不止一点点，主要是错误的性质的误导性比较强。关键是还放在T3！（但它终究是普及组难度的题目）
之前猜了个结论：摆渡车只会在 $t_i$或者$t_i+m$ 时刻停留，然而过不了大样例…
因此我们只能退而求其次了:)
考虑一个合法的转移点的区间会是 $j\in (i-2m,i-m]$ 那么我们很容易得到一个 $O(mt)$ 的做法。这个做法看上去有点悬，但在 CCF 少爷机上大概率是跑的过的。
其实优化的方法也很简单：如果我们发现了一段连续 $m$ 个时刻都没有汽车，那么我们可以直接转移到 $f_i=f_{i-m}$ 。正确性显然，重要的是现在的复杂度就变成了 $O(n{m}^2+t)$ 的。
当然，我们也可以直接用斜率优化做到 $O(t)$ 的复杂度。

2020.10.31

已经准备好退役了。联考的题目出的越来越偏了…
感觉这种极难的比赛（关键是四道题）就是在拼人品，刚好想到了一道相对简单的题目的解法就能得高分…如果每到题目都不深入去想的话甚至连暴力分都来不及拿完。
这不就相当于抽卡拼RP大赛吗…
没办法…出题人操作实在是太恶心了…
这次开题顺序 1-4-3-2 大失败…
正确开题顺序应该是 2-3-1-4 吧…

[LOCAL]宇宙飞船（spaceship）

没什么原因，就是一个想不到的结论题。

其实允许移动只是一个幌子，注意到我们可以随便将被允许的数排列，因此我们可以假设它们不存在。
这样我们就只需要找一个时间单峰的子序列，而这个 LIS 处理一下即可。

[LOCAL]路径计数（counting）

只差一点点就做完了…但是最后才想这题…太迟了…

首先我们很容易得到一个 dp 转移方程：
$$f_{l,r}=\{\begin{array}{ll}r-l+1& \text{if}\forall i,j\in [l,r],a_i=a_j\\ f_{l+1,r}+f_{l,r-1}+1& \text{else}\end{array}$$
这直接做是可以做到 $O(n^2)$ 左右的。
利用这个动态规划计算贡献，考虑我们一开始全都是下面这种情况，那么总方案数显然是 $2^n-1$。
考虑计算由于连续的一段的字符串而产生的 $\text{Δ}$ 值。
由于存在左右两种选择，这显然会是一个组合数的形式，具体呈现如下：

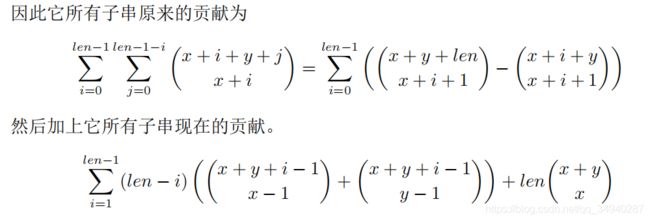
这里面的优化利用了组合数的一个重要性质即其左上到右下的斜线和为斜线正下方与尾部相连的那个数。
$$\sum _{i=0}^r\left(\genfrac{}{}{0ex}{}{n+i}{i}\right)=\left(\genfrac{}{}{0ex}{}{n+r+1}{r}\right)$$
我们利用这个性质差分一下就能把复杂度降下来。
复杂度：$O(n)$。

[LOCAL]编码（code）

如果正式考试又犯了这种错误就完了…

$O(2^k)$ 的部分分很好拿到，只要你不会犯定势思维的错误。