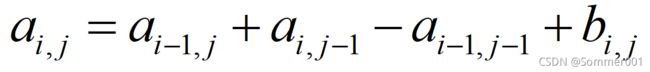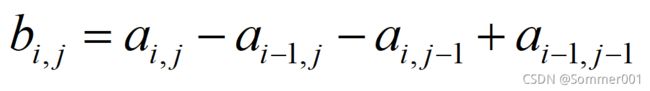二维差分算法最细致解析

解析前提：大家比较明白了一维差分算法和前缀和算法

大家要注意一些编程思维：

首先编程基本运算就是迭代，迭代思维是不考虑边界问题，更重要的是将计算的问题一般化，抽象化，在过程中考虑变量身份。其次就是互逆思维，就比如我们今天讲的前缀和与差分算法，就是一对矛盾，这两个相辅相成，有前缀和矩阵必然存在差分矩阵，两者不能单独分开讨论！

1、差分算法最本质作用是通过差分矩阵随意实现前缀和子矩阵整体数值的增加和减少；

2、差分运算和前缀和运算互为逆运算；

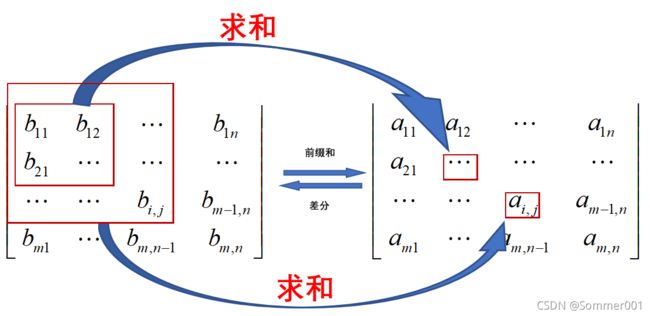
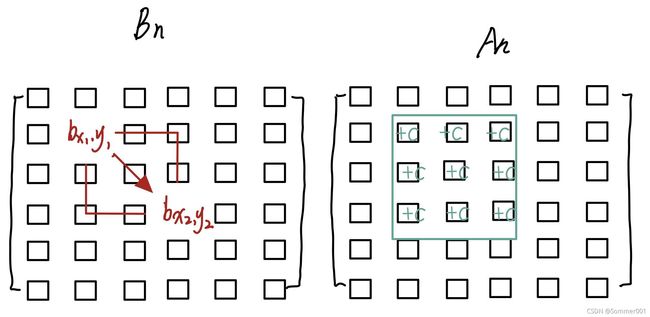
我们假设存在差分矩阵Bn和前缀和矩阵An,则存在一下关系：

  

 从图中我们可以很清晰发现aij 就是b矩阵中bij往左往上所有元素（包括bij所在行所在列）的值的总合，显然往右进行的是前缀和，那么我们怎么用数学表达式表示呢？

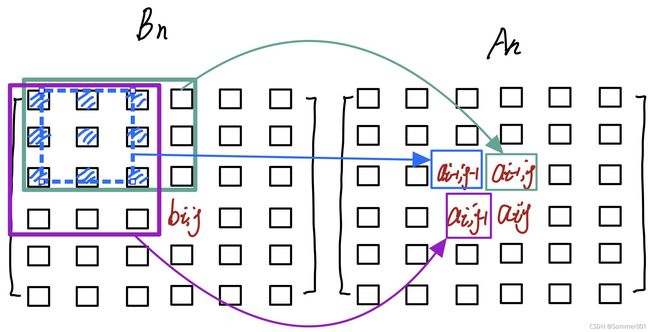
 做一个简单示意图：

 上图表示了一般情况，那么我们可以得到下面的等式：

//对应代码为：
a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j];

 这个等式就将前缀和矩阵和差分矩阵联系在一起，同时体现了迭代思维，由aij之前的值求自身，然后自身又作为已知的值求下一个值，这样我们通过已知差分矩阵Bn得到前缀和矩阵An，同样我们通过该式也可以通过前缀和矩阵An求差分矩阵Bn：

//对应代码为：
b[i][j] = a[i][j] - a[i][j-1] - a[i-1][j] + a[i-1][j-1];

 那么我们利用前缀和矩阵、差分矩阵干什么呢？最简单的：

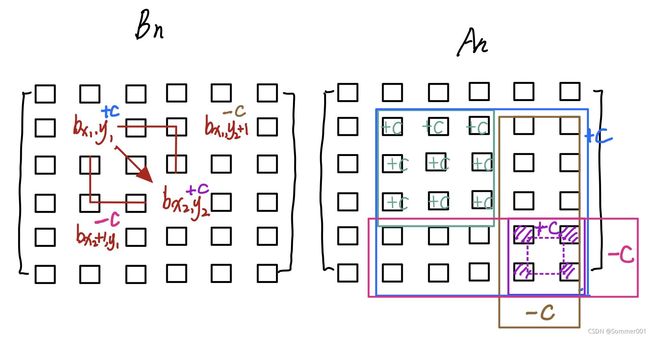
 实现An中从（x1,y1)到（x2,y2)子矩阵同时加上或者减去常数C，或者其他运算，那么怎么通过An和Bn矩阵实现呢：

 通过对差分矩阵元素的的改变进而改变前缀和矩阵元素的值，代码实现形式：

b[x1][y1] += c;
b[x1][y2+1] -= c;
b[x2+1][y1] -= c;
b[x2+1][y2+1] += c;

 Bn矩阵经过这样的变化后，其对应的前缀和子矩阵就会实现+C的操作。但是代码实现起来和你所认为的差分和前缀和很不一样。

题目：首先给定我们一个已知矩阵An，让我们实现其中（x1,y1)到（x2,y2)子矩阵同时增加量为常数C（+C）的的操作。

首先我们第一反应是将给定已知矩阵定义为前缀和矩阵，这样我们就能够将问题转化为上面讨论的：由差分矩阵元素的变化实现前缀和矩阵子矩阵的整体运算操作。那么我们有前缀和矩阵了，必然存在差分矩阵Bn，我们不知道Bn矩阵各个元素是什么，但是它一定存在，而且我们不需要管它是什么形式的（这里很考验编程思维）。

好了，我们现在到了一个很重要的节点，我们来考虑这样一极端个问题：假如给定一个（前缀和）矩阵An(m×n)，其各项元素均为零，那么很显然它的差分矩阵Bn(m×n)也均为零。现在两个矩阵里都很干净，我想给An矩阵中每个元素进行赋值操作，请问有什么方法或者途径呢？很显然，我们通过遍历An矩阵中每个元素，然后赋值就实现了An矩阵的整体赋值。

#include 
using namespace std;
const int N = 10000;  //定义一个较大的数
int m,n;              //定义给定矩阵行数和列数
int a[N][N]；         //定义一个空的二维矩阵


cin >> m >> n;        //输入给定矩阵的行列
for(int i = 1;i <=m ;i++)     //通过遍历实现对An矩阵的赋值操作
   for(int j = 1;j <=n;j++)
            cin >> a[i][j];

但是我们已经学习了通过对一个矩阵的差分矩阵元素的改变，一样可以实现对原来矩阵元素值的改变，只不过我们一直在讲的是改变一个子矩阵整体的值。现在，重点来了！当我们把子矩阵定义为(1×1)的矩阵时，我们居然同样可以实现对An矩阵单个元素的改变（赋值）操作。

这样我们就可以得到两个（本质上是同一个）结论：我们可以通过对一个矩阵的差分矩阵元素的操作既可以实现对原来矩阵的单个元素的操作，也可以实现对该矩阵任意子矩阵中整体元素运算操作！

可能有人会问：我们可以通过差分矩阵间接的操作前缀和矩阵，但是这个算法的前提是：我们需要先通过前缀和矩阵得到差分矩阵，再对差分矩阵元素操作，然后通过操作后的差分矩阵再求前缀和矩阵，最后求得的这个矩阵才是我们想要的，太麻烦了！这样不是绕了更大的弯子了？？

照这么一想，我们感觉这工作量着实听着就很劝退。但是我们从另一个角度想问题，我们知道这个矩阵的差分矩阵存在，但是我们不求，而是利用其身上的一些性质，虚拟出一个看似求出来的差分矩阵Bn，再利用虚拟出来的Bn求我们需要的矩阵，在整个过程中我们并没有求出Bn矩阵的元素值。说起来就很抽象，那么我们一步一步解释：

#include 
using namespace std;
const int N = 10000;  //定义一个较大的数
int m,n;              //定义给定矩阵行数和列数
int a[N][N],b[N][N],g[N][N];//定义三个空的二维矩阵 分别为：前缀和矩阵An，差分矩阵Bn，题目矩阵

//此时我们并不知道给定的An矩阵具体是什么
int n,m;
cin >> m >> n;
for(int i = 1;i<=m;i++)
   for(int j = 1;j<=n;j++)
        cin >> g[i][j];      //这部分属于题目给定我们一个已知矩阵Gn

//到此为止我们有一个已知矩阵
//空矩阵An(用来存放前缀和矩阵)和空矩阵Bn（用来存放差分矩阵）

//我们要知道An必然客观有差分矩阵Bn,那么我们在两者都存在的情况下可以写下面这个函数：
void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1] += c;
    b[x1][y2+1] -= c;
    b[x2][y1+1] -= c;
    b[x2+1][y2+1] += c;
}
//这个函数跟之前讨论的原理（通过差分矩阵改变前缀和矩阵子矩阵的元素值）一致，

int main()

{
//我们怎么利用这个函数呢，当前我们Bn矩阵元素均为零，那么我们可以将函数中定义的
//子矩阵（x1,y1）->(x2,y2) 极端化为1×1的矩阵，也就是参数为（x,y,x,y,c);

for(int i = 1;i<=m;i++)
    for(int j = 1;j<=n;j++)
        insert(i,j,i,j,g[i][j];

//大家试着理解一下这段代码的奥秘，Bn矩阵为零矩阵，我们把一个实际存在的Gn矩阵中的每个元素
//作为一个操作常数C，通过对Bn矩阵中元素进行常数C的操作就相当于给Bn对应的前缀和矩阵An赋值操作。
//我们这样既得到了一个差分矩阵Bn同时也得到了一个前缀和矩阵An,这也侧面说明了，两个矩阵实则为一个！
//很神奇，对不对

//那么我们现在继续对Bn矩阵进行相关操作，达到题目给定要求（实现给定矩阵Gn矩阵中从点（x1,y1）到点(x2,y2)之间的子矩阵所有元素都加上常数C）,就显得很简单了

int x1,y1,x2,y2,c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1,y1,x2,y2,c);      //完成了对Bn矩阵的操作，那么它对应的前缀和矩阵就是我们所求了

//那么问题来了，怎么从差分矩阵得到前缀和矩阵？
//同样可以参考上面我们讲的原理部分（注意查看公式）
for(int i = 1; i<=m; i++)
    for(int j = 1;j<=n;j++)
        a[i][j] = a[i-1][j] + a[i][j-1] + b[i][j] - a[i-1][j-1];

//可能有同学会问：我们并不知道a[i-1][j] ， a[i][j-1]  ，a[i-1][j-1]，这里就是编程的迭代思维
//了，大家可以试着从i= 0，j = 0; 出发一步一步走一遍，就会明白迭代的原理。

//到此为止我们已经得到题目要求的An矩阵了！！！

 希望这样的解释方式能够帮助大家理解，前缀和矩阵和差分矩阵对立统一！！