算法设计与分析习题
1.摆渡的士兵
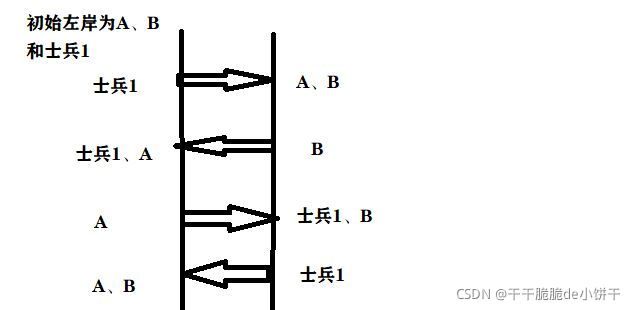
设两个小男孩为A、B,士兵为1,2....12。先考虑士兵1。
四趟可以渡过去一个士兵,所以n个士兵需要4n趟。
2.交替放置的玻璃杯
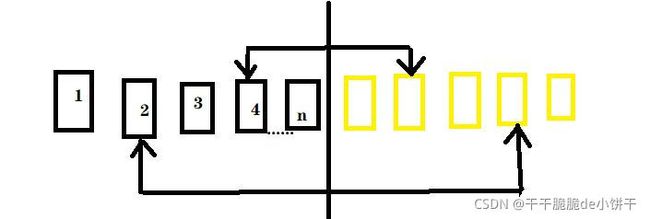
以两种杯子的交界为对称轴,左侧的杯子编号为2的倍数时与右侧对称位置的杯子交换。
当n为奇数时,需要交换的次数是(n-1)/2;
当n为偶数时,需要交换的次数是n/2。
3.标记单元格
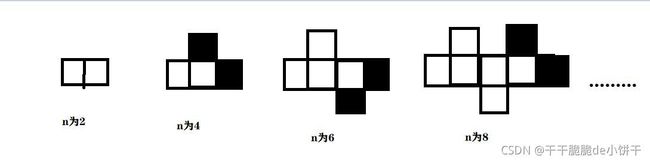
依次类推,n每增加2,按图中规律增加。
n/2(n不为2)为奇数时,水平新增一个单元格,并在其左下方新增一个单元格;
n/2为偶数时,水平新增一个单元格,并在其左上方新增一个单元格。
4.设计减一算法,生成n元素集合的幂集
建立P(n)和P(n-1)幂集的递推关系。
P(n)的幂集等于P(n-1)的幂集+P(n-1)的幂集∪{n}。
8.对于插入排序来说,设计一个限位器避免每次迭代判断边界条件。
应该在带排序数组的第一个元素前面加上一个小于等于最小元素的元素。
效率相同。
习题4.2
1.应用dfs解决有向图的拓扑排序问题。
(a)出栈次序:e f g b c a d
则排序为d a c b g f e
(b)有向图中有闭环,无解。
5.对1中的有向图应用源删除算法
先删除d 再删除a 删除b 删除c 删除g 删除f 删除e.
排序为dacbgfe
10.蛛网问题
对该有向图进行拓扑排序,左右对称可以只看左半边图。
方法是对所有前驱结点的路径求和。
S(1)—A(1)—B(1)—E(1)—G(1)—H(3)—O(11)—I(14)—C(15)—J(25)—D(40)—K(61)—F(141)。
共有141条路径
习题4.3
9.生成4位的二进制反射格雷码
a.0000,0001,0011,0010,0110,0111,0101,0100,
1100,1101,1111,1110,1010,1011,1001,1000
b.非递归算法求格雷码i
i 0 1 2 3 4 5 6 7
ii的二进制编码 0 1 10 11 100 101 110 111
格雷码 0000 0001 0011 0010 0110 0111 0101 0100
i
i 8 9 10 11 12 13 14 15
ii的二进制编码 1000 1001 1010 1011 1100 1101 1110 1111
格雷码 1100 1101 1111 1110 1010 1011 1001 1000
习题4.4
3.折半查找
a.四次
b.3、27、42、74、85、98
c.(4x6+3x4+2x2+1x1)/13=3.15次
d.(4×12+3×2)/14≈3.86次
10.假币问题
11.
a.俄式乘法计算26×47
26×47=13×94=6×188=3×376=1×752
752+376+94=1222
b.没有
习题4.5
6.
a.n>2的32次方
b.当n趋于无穷大的时候,log log n/log n趋向于0。故选i
12.翻薄饼
数组翻转问题
先查找到最大的薄饼,
若在最下面,则不需要操作;
若在最上面,则只需将整个数组翻转;
若在中间,则先将该饼以及它上面的饼整体翻转,将最大的饼翻转到最上面,然后再进行一次翻转翻到最下面。
最大的薄饼归位之后。将剩下的饼看做一个新的数组,重复上述操作,可实现题目要求。