最短路径(Dijkstra算法)

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

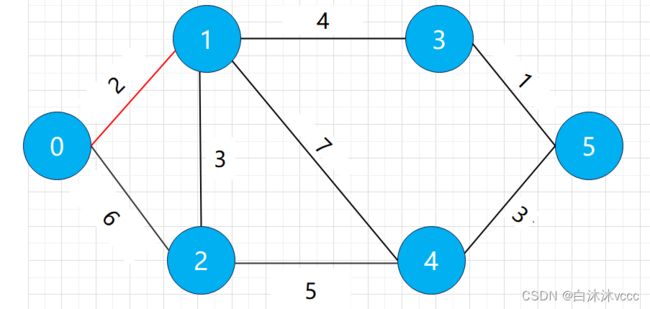
迪杰斯特拉算法采用的是贪心算法，对于最短路径来说，就是求出发点到终点过程中的每一步的最优解。本次就以最短路径为例，假设要求0到5的最短路径，图示如下：

思路：将起点作为第一个标记点，其余点均为未标记点。以最初标记点为对象，遍历未标记点，寻找距离最初标记点最近的未标记点并将这个未标记点变为标记点，且两点之间的路径为最优解(注：最后求出的是起点到所有点的最短路径)。

分析：如图，0为标记点，其余点均为未标记点，其中未标记点1离0最近，将1纳入标记点。并可知1的父节点为0。

以0,1为连接点，从未标记继续寻找下一个到起点0最近的未标记点2(此处如有疑惑，先继续看)，将2纳入标记点。并可知2的父节点为1。

继续以0,1,2为连接点，寻找离0最近的未标记点3，将3纳入标记点,并可知3的父节点为1。

继续以0,1,2,3为连接点，寻找离0最近的未标记点5，将5纳入标记点。并可知5的父节点为3.

继续以0,1,2,3,5为连接点，寻找离0最近的未标记点4，将4纳入标记点。并可知4的父节点为1。

此时所有结点都转化为了标记点，到此我们已经找到了起点0到各个点的最短路径。根据上述的父子关系则可逆推出最短路径。以0到5为例:5的父亲为3，可推5->3。3的父亲为1，可推出5->3->1。又1的父亲为0，即5->3->1->0。将其逆序，则可得出最短路径0->1->3->5。

代码实现(C语言)：

//Dijsktra算法
//最短路径
#include
#include
#define N 100

typedef int ElementType;

typedef struct Ver {
	struct Ver *father;
	char ch;
	int id;
	int minLength;
	int flag;//表示给结点是否被标记,0表示未被标记，1 标记
} Ver,*Vertex;

//初始化城市结点,并接收城市个数
int InitialCitys(Vertex vertex[]) {
	int m,i=0;//'m'城市数量
	printf("请输入城市数量:");
	scanf("%d",&m);
	//初始化vertex,给vertex分配空间
	for(i=0; iminLength=99999;//假设99999为无穷大
		vertex[i]->flag=0;
	}
	printf("\n请输入城市名称:");
	i=0;
	while(ich=c;
		vertex[i]->id=i;
		i++;
	}
	return m;
}

//根据城市名称获取对应下标
int getCityIndex(Vertex vertex[],char ch,int m) {
	for(int i=0; ich==ch) return vertex[i]->id;
	}
}

//初始化路径，并接收路径个数
void InitialPath(ElementType path[][N],Vertex vertex[],int m) {
	int n,i,j;
	//初始化path
	for(int i=0; iB):");
	char c;
	//消除空格和回车
	while((c=getchar())==' '||c=='\n');
	*start=c;
	while((c=getchar())==' '||c=='\n');
	*end=c;
	//将起点标记
	int t=getCityIndex(vertex,start[0],m);
	vertex[t]->flag=1;
	vertex[t]->minLength=0;
	vertex[t]->father=NULL;
	return;
}

//建立最短路径
void BuildShortPath(Vertex vertex[],ElementType path[][N],char start,char end,int m) {
	//遍历每个结点共需要循环m-1次
	//每次遍历将未标记点转化为标记点
	for(int i=1; iflag==0) {
				//遍历已标记
				for(int k=0; kflag!=0) {
						//求出该未标记点到标记点的最短距离
						//如果两城市之间距离小于最小距离，则更新最短距离
						int all_p=path[k][j]+vertex[k]->minLength;
						if(all_pminLength) {
							vertex[j]->minLength=all_p;
							vertex[j]->father=vertex[k];
						}
					}
				}

				//判断该未标记点是否是所有未标记点到标记点的最短距离
				if(vertex[j]->minLengthminLength;
					t=j;
				}
			}
		}
		vertex[t]->flag=1;
//		printf("第%d次标点为%c,父亲为:%c,路径长度为%d\n",i,vertex[t]->ch,vertex[t]->father->ch,vertex[t]->minLength);
	}
}

//输出单个或全部最短路径
void PrintAllPath(Vertex vertex[],char start,int m,int front,int tail) {
	if(tail-front==1) printf("%c到%c最短路径为：",start,vertex[front]->ch);
	else
		printf("\n\n*以下是%c到 各个点的最短路径*:\n",start);
	//指定输出最短路径的范围
	for(int i=front; ich;
		//如果起点和终点相同，则退出
		if(end==start) continue;
		printf("%c到%c最短路径为：",start,end);
		int j=getCityIndex(vertex,end,m);
		Vertex p=vertex[j];
		int minLength=p->minLength;
		int n=0;
		char ch[N];
		//因为结果是逆序的，所以要颠倒一下
		while(p!=NULL) {
			ch[n++]=p->ch;
			p=p->father;
		}
		printf("%c",ch[n-1]);
		for(int i=n-2; i>=0; i--) {
			printf("->%c",ch[i]);
		}
		printf("\n最短路径长度为:%d\n",minLength);
	}
}

int main() {
	//定义vertex指针型结构体数组,并分配空间
	Vertex vertex[N];
	//初始化城市结点,并接收城市个数
	int m=InitialCitys(vertex);
	//用处存储两个数之间的距离
	ElementType path[N][N];
	//初始化路径，并接收路径个数
	InitialPath(path,vertex,m);
	//输入起点和终点,并将每个城市初始结点至为start
	char start,end;
	InputStartAndEnd(&start,&end,vertex,m);
	//建立最短路径
	BuildShortPath(vertex,path,start,end,m);
	//获取end的下标
	int tail=getCityIndex(vertex,end,m);
	//输出最短路径
	PrintAllPath(vertex,start,m,tail,tail+1);
	//输出全部最短路径
	PrintAllPath(vertex,start,m,0,m);
}

C语言测试数据：

6
012345
8
012
026
123
134
147
245
351
453
05

代码实现(Java)：

import java.util.ArrayList;
import java.util.List;
 
public class Dijkstra {
 
    static int[][] matrix = new int[6][6];
    final static int N = 10000;
 
    public static void main(String[] args) {
 
        //邻接矩阵
        matrix[0] = new int[]{N, 2, 6, N, N, N};/*0*/
        matrix[1] = new int[]{2, N, 3, 4, 7, N};/*1*/
        matrix[2] = new int[]{6, 3, N, N, 5, N};/*2*/
        matrix[3] = new int[]{N, 4, N, N, N, 1};/*3*/
        matrix[4] = new int[]{N, 7, 5, N, N, 3};/*4*/
        matrix[5] = new int[]{N, N, N, 1, 3, N};/*5*/
 
        //已标记点集合
        List Marked = new ArrayList<>();
        Vertex vt0 = new Vertex();
        vt0.id = 0;
        vt0.minLenth = 0;
        Marked.add(vt0);
 
        //未标记点集合
        List UnMarked = new ArrayList<>();
        for (int i = 0; i < 5; i++) {
            Vertex vtx = new Vertex();
            vtx.id = i+1;
            UnMarked.add(vtx);
        }
 
        //将未标记点集合中的点转移到已标记点集合
        int order = 1;
        while(!UnMarked.isEmpty()){
            Vertex vtx = FindVer(Marked, UnMarked);
            UnMarked.remove(vtx);
            Marked.add(vtx);
            System.out.println("第"+order+"次标号，顶点"+vtx.id+"的标号为：（" + vtx.father.id + "，" +vtx.minLenth + "）");
            order++;
        }
 
        //输出路径
        for(Vertex v :Marked){
            if(v.id == 5){
                System.out.println("0-5的最短路径长度为：" + v.minLenth);
                System.out.print("逆推得最优路径为：" + "5");
                while(v.id != 0){
                    v = v.father;
                    System.out.print( " -> " + v.id);
                }
            }
        } 
    }
 
    static Vertex FindVer(List Marked, List UnMarked){
        int M = 10000;
        Vertex v = null;
        for (Vertex ve : UnMarked) {
            for (Vertex vr : Marked) {
                int all_p = vr.minLenth + matrix[vr.id][ve.id];
                if (all_p <= ve.minLenth) {
                    ve.minLenth = all_p;
                    ve.father = vr;
                }
            }
            if (ve.minLenth < M) {
                M = ve.minLenth;
                v = ve;
            }
        }
        return v;
    }
 
}
class Vertex {
    public int id;
    public Vertex father;
    public int minLenth = 10000;
}

一言：

邂逅的频繁，谁知那并非偶然。